Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-11T10:03:38.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Remark on the Tricomi Equation

Published online by Cambridge University Press:  22 January 2016

Tadato Matsuzawa
Tadato Matsuzawa*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

As an application of the Garleman-type estimation Hörmander [4], p. 221, has proved the following:

A solution (distribution) of the Tricomi equation

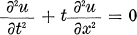
in an open set Ω in 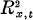belongs to C∞(Ω) if it is in C∞(Ω-) where .

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 48 , December 1972 , pp. 91 - 97
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1972

References

[1] Baouendi, M. S., Sur une class d’opérateurs elliptiques dégénérés, Bull. Soc. Math. France, 95, 45–87 (1967).Google Scholar
[2] Berezin, I. S., On Cauchy’s problem for linear equations of the second order with initial conditions on a parabolic line (in Russian). Mat. Sbornik, N. S. t24 (66), 301–320 (1949).Google Scholar
[3] Courant, R. and Hilbert, D. : Methods of mathematical phisics. Vol. II. Inter-science Pub. New York (1962).Google Scholar
[4] Hörmander, L. : Linear partial differential operators. Berlin, Springer-Verlag (1963).Google Scholar
[5] Matsuzawa, T., Sur les équations utt+tαuxx= f (α≧0) . Nagoya Math. J. Vol. 42, (1971).Google Scholar
[6] Matsuzawa, T., Sur les équations quasi-elliptiques et les classes de Gevrey. Bull. Soc. Math. France, t96, 243–263 (1968).Google Scholar