No CrossRef data available.
Published online by Cambridge University Press: 23 May 2024
Let 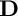 $\mathbf {D}$ be a bounded homogeneous domain in
$\mathbf {D}$ be a bounded homogeneous domain in 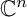 ${\mathbb {C}}^n$. In this note, we give a characterization of the Stein domains in
${\mathbb {C}}^n$. In this note, we give a characterization of the Stein domains in 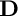 $\mathbf {D}$ which are invariant under a maximal unipotent subgroup N of
$\mathbf {D}$ which are invariant under a maximal unipotent subgroup N of 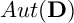 $Aut(\mathbf {D})$. We also exhibit an N-invariant potential of the Bergman metric of
$Aut(\mathbf {D})$. We also exhibit an N-invariant potential of the Bergman metric of 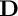 $\mathbf {D}$, expressed in a Lie theoretical fashion. These results extend the ones previously obtained by the authors in the symmetric case.
$\mathbf {D}$, expressed in a Lie theoretical fashion. These results extend the ones previously obtained by the authors in the symmetric case.