Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T23:05:24.075Z Has data issue: false hasContentIssue false
  • English
  • Français

A Remark on Relative Homology and Cohomology Groups of a Group

Published online by Cambridge University Press:  22 January 2016

Tadasi Nakayama
Tadasi Nakayama*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a group and H a subgroup of G. With a left G-module M, relative cohomology groups Hn(G, H, M) of G on M, relative to H, have been defined by Adamson [1] and may be expressed as 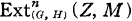(Z, M) in the notation of relative homological algebra of Hochschild [2], where Z denotes the G-module of rational integers (acted by G trivially). Regarding M as a right G-module, 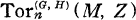(M, Z) are similarly relative homology groups Hn(G, H, M). In case H is of finite index in G, Hochschild [2] defines further negative-dimensional relative homology and cohomology groups.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 16 , February 1960 , pp. 1 - 9
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1960

References

[1] Adamson, I. T., Cohomology theory for non-normal subgroups and non-normal fields, Proc. Glasgow Math. Assoc. 2 (1954-6), 67–76.CrossRefGoogle Scholar
[2] Hochschild, G., Relative homological algebra, Trans. Amer. Math. Soc. 82 (1956), 246–269.CrossRefGoogle Scholar