Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T21:50:13.292Z Has data issue: false hasContentIssue false
  • English
  • Français

Rees algebras of non-singular equimultiple prime ideals*

Published online by Cambridge University Press:  22 January 2016

M. Herrman, ,
J. Ribbe  and
N.V. Trung
M. Herrman,
Affiliation:
Mathematisches Institut der Universität zu Köln, 5000 Köln 41, Germany
J. Ribbe
Affiliation:
Mathematisches Institut der Universität zu Köln, 5000 Köli 41, Germany
N.V. Trung
Affiliation:
Institute of Mathematics, Box 631, Bò Hô, Hanoi Vietnam
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent paper [HI2] the first named author and S. Ikeda have investigated Gorenstein properties under blowing up of height two equimultiple ideals from the arithmetical point of view. The problem is to what extent does the Gorenstein property of the Rees algebra R(a) = 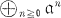of an equimultiple ideal a of a local ring (A, m) describe the structure of A and a. One result is that if A is a generalized Cohen-Mac aulay ring (i.e. a ring of finite local cohomology) with dim (A) ⊇ 4 and if there is an height two equimultiple prime ideal p such that R(p) is Gorenstein, then A is Gorenstein and p is generated by a regular sequence (see [HI2], Theorem 2.6). That has led to the question whether this result is still valid for dim (∧) = 3. ∧ partial answer was given in [HI2], Proposition 2.10, where “equimultiplicity” was replaced by the stronger condition “p/p2 is flat over A/p”

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 124 , December 1991 , pp. 1 - 12
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1991

Footnotes

*

We thank the referee for his detailed suggestions and improvements.

References

[CST] Cuong, N. T., Schenzel, P., Trung, N. V., Verallgemeinerte Cohen-Macaulay-Moduln, Math. Nachr., 85 (1978), 57–73.Google Scholar
[HI1] Herrmann, M., Ikeda, S., Remarks on liftings of Cohen-Macaulay property, Nagoya Math. J., 9, 2 (1983), 121–132.CrossRefGoogle Scholar
[HI2] Herrmann, M., Ikeda, S., On the Gorenstein property of Rees algebras, Manuscripta math., 59 (1987), 471–490.CrossRefGoogle Scholar
[HIO] Herrmann, M., Ikeda, S., Orbanz, U., Equimultiplicity and blowing up, (Springer, Berlin-Heidelberg-New York, 1988).CrossRefGoogle Scholar
[HMV] Herrmann, M., Moonen, B., Villamayor, O., Ideals of linear type and some variants, Queen’s papers in Pure and Appl. Math. Nr. 83. The Curves Seminar at Queen’s, Vol. VI, 1989.Google Scholar
[I] Ikeda, S., On the Gorensteinness of Rees algebras over local rings, Nagoya Math. J., 102 (1986), 135–154.CrossRefGoogle Scholar
[T] Trung, N. V., Über die Übertragung von Ringeigenschaften zwischen R und R/(F), Math. Nachr., 92 (1979), 215–229.CrossRefGoogle Scholar
[TI] Trung, N. V., Ikeda, S., When is the Rees algebra Cohen-Macaulay?, Comm. Alg., 17 (12) (1989), 2893–2922.CrossRefGoogle Scholar