Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-20T13:41:35.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Real canonical cycle and asymptotics of oscillating integrals

Published online by Cambridge University Press:  22 January 2016

Daniel Barlet
Daniel Barlet*
Affiliation:
Universit Henri Poincaré et Institut Universitaire de France, Institut Elie Cartan UMR 7502 UHP-CNRS-INRIA, BP 239 - F - 54506, Vandœuvre-lès-Nancy Cedex, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Xℝ ⊂ ℝN a real analytic set such that its complexification Xℂ ⊂ ℂN is normal with an isolated singularity at 0. Let fℝ : Xℝ → ℝ a real analytic function such that its complexification fℂ : Xℂ → ℂ has an isolated singularity at 0 in Xℂ. Assuming an orientation given on 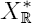to a connected component A of 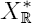we associate a compact cycle Γ(A) in the Milnor fiber of fℂ which determines completely the poles of the meromorphic extension of 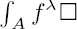or equivalently the asymptotics when T → ±∞ of the oscillating integrals 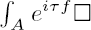. A topological construction of Γ(A) is given. This completes the results of [BM] paragraph 6.

Keywords

32S4014P15
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 171 , 2003 , pp. 187 - 196
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2003

References

[B99] Barlet, D., Multiple poles at negative integers for in the case of an almost isolated singularity, Publ. Res. Inst. Math. Sci., 35 (1999), 571–584.CrossRefGoogle Scholar
[BM] Barlet, D. and Maire, H. M., Non trivial simple poles at negative integers and mass concentration at singularity, Math. Ann., 323 (2002), 547–587.Google Scholar
[J] Jeddi, A., Preuve d’une conjecture de Palamodov, Topology, 41 (2002), 271–306.CrossRefGoogle Scholar
[P] Palamodov, V. P., Asymptotic expansions of integrals on complex and real regions, Math USSR, 55 (1986), 201–236.Google Scholar