Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T23:32:49.794Z Has data issue: false hasContentIssue false
  • English
  • Français

Rank 2 symmetric hyperbolic Kac-Moody algebras

Published online by Cambridge University Press:  22 January 2016

Seok-Jin Kang  and
Duncan J. Melville
Seok-Jin Kang*
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, IN 46556, U.S.A.
Duncan J. Melville
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, IN 46556, U.S.A.
*
Department of Mathematics, College of Natural Sciences, Seoul National University, Seoul 151-742, Korea
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

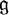Affine Kac-Moody algebras represent a well-trodden and well-understood littoral beyond which stretches the vast, chaotic, and poorly-understood ocean of indefinite Kac-Moody algebras. The simplest indefinite Kac-Moody algebras are the rank 2 Kac-Moody algebras (a) (a ≥ 3) with symmetric Cartan matrix 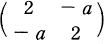, which form part of the class known as hyperbolic Kac-Moody algebras. In this paper, we probe deeply into the structure of those algebras 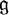(a), the e. coli of indefinite Kac-Moody algebras. Using Berman-Moody’s formula ([BM]), we derive a purely combinatorial closed form formula for the root multiplicities of the algebra 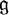(a), and illustrate some of the rich relationships that exist among root multiplicities, both within a single algebra and between different algebras in the class. We also give an explicit description of the root system of the algebra (a). As a by-product, we obtain a simple algorithm to find the integral points on certain hyperbolas.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 140 , December 1995 , pp. 41 - 75
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

Footnotes

*

Supported in part by Basic Science Research Institute Probram, Ministry of Education of Korea, BSRI-94-1414 and GARC-KOSEF at Seoul National University, Korea.

References

[BKM] Benkart, G. M., Kang, S.-J., Misra, K. C., Graded Lie algebras of Kac-Moody type, Adv. in Math., 97 (1993), 154–190.Google Scholar
[BM] Berman, S., Moody, R. V., Multiplicities in Lie alebras, Proc. Amer. Math. Soc, 76 (1979), 223–228.Google Scholar
[F] Feingold, A. J., A hyperbolic GCM and the Fibonacci numbers, Proc. Amer. Math. Soc, 80 (1980), 379–385.Google Scholar
[FF] Feingold, A. J., Frenkel, I. B., A hyperbolic Kac-Moody algebra and the theory of Siegel modular forms of genus 2, Math. Ann., 263 (1983), 87–144.Google Scholar
[FFR] Feingold, A. J., Frenkel, I. B., Ries, J. F. X., Representations of hyperbolic Kac-Moody algebras, J. Algebra, 156 (1993), 433–453.CrossRefGoogle Scholar
[Fr] Frenkel, I. B., Representations of Kac-Moody algebras and dual resonance models, Applications of Group Theory in Physics and Mathematical Physics, Lectures in Applied Math., Amer. Math. Soc, 21 (1985), 325–353.Google Scholar
[GK] Gabber, O., Kac, V. G., On defining relations of certain infinite dimensional Lie algebras, Bull. Amer. Math. Soc, 5 (1981), 185–189.Google Scholar
[GL] Garland, H., Lepowsky, J., Lie algebra homology and the Macdonald-Kac formulas, Invent. Math., 34 (1976), 37–76.CrossRefGoogle Scholar
[K] Kac, V. G., Infinite dimensional Lie algebras, 3rd ed. Cambridge University Press (1990).CrossRefGoogle Scholar
[KMW] Kac, V. G., Moody, R. V., Wakimoto, M., On E 10 , Differential Geometrical Methods in Theoretical Physics, Bleuler, Werner, K. M. (eds.), Kluwer Academic Publishers (1988), 109–128.Google Scholar
[Ka1] Kang, S.-J., Kac-Moody Lie algebras, spectral sequences, and the Witt formula, Trans. Amer. Math. Soc, 339 (1993), 463–495.Google Scholar
[Ka2] Kang, S.-J., Root multiplicities of Kac-Moody algebras, Duke Math. J., 74, No. 3 (1994), 635–666.CrossRefGoogle Scholar
[KM] Kang, S.-J., Melville, D. J., Root multiplicities of the Kac-Moody algebras HAn , J. Algebra. 170 (1994), 277–299.CrossRefGoogle Scholar
[LM] Lepowsky, J., Moody, R. V., Hyperbolic Lie algebras and quasi-regular cusps on Hilbert modular sufaces, Math. Ann., 245 (1979) 63–88.Google Scholar
[Li] Liu, L. -S., Kostant’s formula for Kac-Moody Lie algebras, J. Algebra, 149 (1992), 155–178.CrossRefGoogle Scholar
[M] Moody, R. V., Root systems of hyperbolic type, Adv. in Math., 33 (1979), 144–160.Google Scholar
[Se] Serre, J. P., Lie Algebras and Lie Groups, 1964 Lectures given at Harvard University, Benjamin, New York (1965).Google Scholar