Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T23:44:59.711Z Has data issue: false hasContentIssue false
  • English
  • Français

Random integral representations for classes of limit distributions similar to Lévy class L0, II

Published online by Cambridge University Press:  22 January 2016

Zbigniew J. Jurek
Zbigniew J. Jurek*
Affiliation:
Institute of Mathematics, University of Wroclaw, 50384 Wroclaw, Poland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ξ(t) and η(t) be two stochastic processes such that ξ has stationary independent increments and ξ(0) = 0 a.s. Suppose that 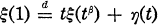for each 0 < t ≤ 1, with ξ(tβ) independent of η(t) and a fixed parameter β ∈ (−2, 0). It is shown that ξ(1) satisfies the above equation if and only if ξ(1) is a sum of two independent r.v.’s: strictly stable one with the exponent – β and the one given by a random integral 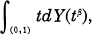where Y has stationary independent increments and E [|| Y(1)||-β] < ∞.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 114 , June 1989 , pp. 53 - 64
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1989

References

[1] Araujo, A. and Gine, E., The central limit theorem for real and Banach space valued random variables; John Wiley, New York, 1980.Google Scholar
[2] deAcosta, A., Exponential moments of vector valued random series and triangular arrays, Ann. Probab., 8 (1980), 381–389.Google Scholar
[3] Jurek, Z. J., Relations between the s-selfdecomposable and self-decomposable measures, Ann. Probab., 13 (1985), 592–608.CrossRefGoogle Scholar
[4] Jurek, Z. J., Random integral representations for classes of limit distributions similar to Lévy class L0 , Probab. Theory Rel. Fields, 78 (1988), 473–490.CrossRefGoogle Scholar
[5] Jurek, Z. J. and Vervaat, W., An integral representation for selfdecomposable Banach space valued random variables, Z. Wahrsch. Verw. Gebiete, 62 (1983), 247–262.CrossRefGoogle Scholar
[6] O’Connor, T. A., Infinitely divisible distributions similar to class L, ibid., 50 (1979), 265–271.Google Scholar
[7] Parthasarathy, K. R., Probability measures on metric spaces; Academic Press, New York-London, 1967.Google Scholar
[8] Pollard, D., Convergence of stochastic processes, Springer Series in Statistics; Springer-Verlag, New York, 1984.Google Scholar
[9] Prakasa, Rao, B. L. S., Characterization of stochastic processes by stochastic integrals, Adv. Appl. Probab., 15 (1983), 81–98.Google Scholar