Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T23:23:23.594Z Has data issue: false hasContentIssue false
  • English
  • Français

Radial Limits of Quasiconformal Functions

Published online by Cambridge University Press:  22 January 2016

D. A. Storvick
D. A. Storvick*
Affiliation:
Mathematics Research Center U.S. Army, University of Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Beurling and Ahlfors [1] answered a fundamental question concerning the boundary correspondence induced by a quasiconformal mapping when they proved that the correspondence need not be given by an absolutely continuous function. They proved this by characterizing the boundary correspondences of quasiconformal mappings of the upper half-plane lm(z)>0 onto the upper half-plane lm(w)>0 under which the boundary points at infinity correspond. They proved that a necessary and sufficient condition that the strictly monotone increasing function μ(x) carrying the real axis onto itself be the boundary correspondence induced by such a quasiconformal mapping is that μ(X) should satisfy a ρ-condition

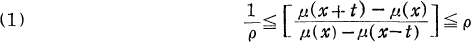
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 23 , December 1963 , pp. 199 - 206
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1963

References

[1] Beurling, A. and Ahlfors, L.: The boundary correspondence under quasiconformal mappings. Acta Math. 96 (1956), 125–142.CrossRefGoogle Scholar
[2] Cartwright, M. L. and Collingwood, E. F.: The radial limits of functions meromorphic in a circular disc. Math. Zeitschr. 76 (1961), 404–410.CrossRefGoogle Scholar
[3] Collingwood, E. F.: Cluster sets and prime ends. Ann. Acad. Sci. Fenn. Ser. A.l. 250/6 (1958), 1–11.Google Scholar
[4] Collingwood, E. F. and Cartwright, M. L.: Boundary theorems for a function meromorphic in the unit circle. Acta Math. 87 (1952), 83–146.CrossRefGoogle Scholar
[5] Künzi, H.: Quasikonforme Abbildungen. Springer-Verlag, Berlin (1960).CrossRefGoogle Scholar
[6] Lehto, O.: On the differentiability of quasiconformal mappings with prescribed com- plex dilatation. Ann Acad. Sci. Fenn. Ser. A. I. 275 (1960), 1–27.Google Scholar
[7] Mori, A.: On quasi-conformality and pseudo-analyticity. Trans. Amer. Math. Soc. 84 (1956), 56–77.CrossRefGoogle Scholar
[8] Nevanlinna, R.: Eindeutige analytische Funktionen, 2nd Auf. Springer-Verlag, Berlin (1953).Google Scholar
[9] Noshiro, K.: Cluster sets. Springer-Verlag, Berlin (1960).CrossRefGoogle Scholar
[10] Privalov, I. I: Sur quelques applications de la mesure harmonique des ensembles de points à certains problèmes de la théorie des fonctions. Rec. Math. Moscou, N. s. (3) (Russian; French summary 533) (1938), 527–532.Google Scholar
[11] Privalov, I. I.: Randeigenschaften analytischer Funktionen. (Ubersetzung aus dem Russischen), Deutscher Verlag der Wissenschaften, Berlin (1956).Google Scholar
[12] Saks, S.: Theory of the integral, Stechert, New York (1937).Google Scholar
[13] Stoïlow, S.: Leçons sur les principes topologiques de la théorie des fonctions analytiques. Gauthier-Villars, Paris (1938).Google Scholar
[14] Storvick, D. A.: On pseudo-analytic fnnctions. Nagoya Math. J. 12 (1957), 131–138.CrossRefGoogle Scholar