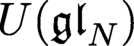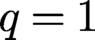Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Li, Yiqiang
2021.
Quasi-split symmetric pairs of 𝑈(𝔰𝔩_{𝔫}) and Steinberg varieties of classical type.
Representation Theory of the American Mathematical Society,
Vol. 25,
Issue. 32,
p.
903.