Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T23:42:22.458Z Has data issue: false hasContentIssue false
  • English
  • Français

A quasianalytic singular spectrum with respect to the Denjoy-Carleman class

Published online by Cambridge University Press:  22 January 2016

Soon-Yeong Chung  and
Dohan Kim
Soon-Yeong Chung
Affiliation:
Department of Mathematics, Sogang University, Seoul 121-742, Korea, [email protected]
Dohan Kim
Affiliation:
Department of Mathematics, Seoul National University, Seoul 151-742, Korea, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Making use of the FBI (Fourier-Bros-Iagolnitzer) transforms we simplify the quasianalytic singular spectrum for the Fourier hyperfunctions, which was defined for distributions by Hörmander as follows; for any Fourier hyperfunction u, (x0, ξ0) does not belong to the quasianalytic singular spectrum W FM(u) if and only if there exist positive constants C, γ and N, and a neighborhood of x0 and a conic neighborhood Г of ξ0 such that

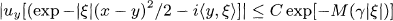
for all x ∈ U, |ξ| ∈ Γ and |ξ| ≥ N, where M(t) is the associated function of the defining sequence Mp. This result simplifies Hörmander’s definition and unify the singular spectra for the C∞ class, the analytic class and the Denjoy-Carleman class, both quasianalytic and nonquasianalytic.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 148 , December 1997 , pp. 137 - 149
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1997

References

[B] Bony, J. M., Equivalence des diverses notions de spectre singulier analytique, Sém. Goulaouic-Schwartz 1975-1976, Exposé no. 3.Google Scholar
[CCK] Chung, J., Chung, S.-Y. and Kim, D., A characterization for Fourier hyperfunctions, Publ. RIMS, Kyoto Univ., 30 (1994), 203–208.Google Scholar
[H1] Hörmander, L., Fourier integral operators I, Acta. Math., 127 (1971), 79–183.Google Scholar
[H2] Hörmander, L., Uniqueness theorems and wave front sets for solutions of linear partial differential equations with analytic coefficients, Comm. Pure Appl. Math., 24 (1971), 671–704.Google Scholar
[H3] Hörmander, L., Between distributions and hyperfunctions, Astérisque, 131 (1985), 89–106.Google Scholar
[H4] Hörmander, L., The analysis of linear partial differential operators I, Springer-Verlag, Berlin-New York, 1983.Google Scholar
[I] Iagolnitzer, D., Microlocal essential support of distribution and decomposition theorem an introduction, Lecture Notes in Math., vol. 449, Springer-Verlag, Berlin and New York, 1975, 121–132.Google Scholar
[Ka] Kawai, T., On the theory of Fourier hyperfunctions and its applications to partial differential equations with constant coefficients, J. Fac. Sci. Univ. Tokyo, Sect. IA, 17 (1970), 467–517.Google Scholar
[KCK] Kim, K.W., Chung, S.Y. and Kim, D., Fourier hyperfunctions as the boundary values of smooth solutions of the heat equation, Publ. RIMS, Kyoto Univ., 29 (1993), 289–300.Google Scholar
[Ko] Komatsu, H., Ultradistributions I, J. Fac. Sci. Univ. Tokyo, Sect IA, 20 (1973), 25–105.Google Scholar
[KP] Krantz, S. and Parks, H., A primer of real analytic functions, Birkhäuser, Basel, 1992.Google Scholar
[M] Matsuzawa, T. II, Trans. Amer. Math. Soc., 313 (1989), 619–654.Google Scholar
[Sa] Sato, M., Hyperfunctions and partial differential equations, Proc. Int. Conf. on Funct. Anal, and Rel. Topics, Univ. of Tokyo Press, Tokyo, 1969, pp. 91–94.Google Scholar
[S] Sjöstrand, J., Propagation of analytic singularities for second order Dirichlet problems, Comm. Partial Differential Equations, 5 (1980), 41–94.CrossRefGoogle Scholar