Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T00:01:28.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Propriétés des Solutions Faibles Non Négatives de L’équation Parabolique

Published online by Cambridge University Press:  22 January 2016

J. Chabrowski
J. Chabrowski*
Affiliation:
Université Silésienne, Katowice
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Le but de cette communication est de prouver que la solution u(t, x) faible non négative dans (0,T]=En de l’équation

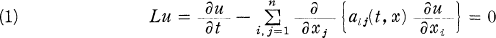
possède la limite presque partout dans En si t converge vers zéro, ainsi qu’elle représentable sous la forme d’une intégrale de la solution fondamentale faible de (1) par rapport à une mesure non négative. Ces problèmes ont été traités par M. Kato et M. Krzyzanski (voir [7] et [8]) pour les solutions au sens classiques. Nos démonstrations sont basées sur les méthodes utilisées dans leurs travaux.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 39 , August 1970 , pp. 119 - 125
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1970

References

Travaux Cités

[1] Aronson, D.G., On the Green’s fonction for second order parabolic differential equations with discontinuous coefficients, Bull. Am. Math. Soc., 69 (1963), p. 841–847.Google Scholar
[2] Aronson, D.G., Uniqueness of positive weak solutions of second order parabolic equations, Ann. Polon. Math., XVI (1965), p. 285–303.CrossRefGoogle Scholar
[3] Aronson, D.G., Isolated singularities of solutions of second order parabolic equations, Arch. Rational Mech. Anal., 19 (1965), p. 231–238.Google Scholar
[4] Aronson, D.G., Bounds for the fundamental solution of a parabolic equation, Bull. Am. Math. Soc., 73 (1967), p. 890–896.CrossRefGoogle Scholar
[5] Bourbaki, N., Éléments de Mathématique, XIII, livre VI, Intégration Paris, 1952.Google Scholar
[6] Fiedrichs, K.O., The identity of weak and strong extensions of differential operators, Tran. Am. Math. Soc., 55 (1944), p. 132–151.Google Scholar
[7] Kato, M., On positive solutions of the heat equation, Nagoya Math. Journ., 30 (1967), p. 203–207.Google Scholar
[8] Krzyzanski, M., Sur les solutions non négatives de l’équation linéaire normale parabolique, Revue Roumaine Math. Pures Appl., IX (1964), p. 393–408.Google Scholar
[9] Moser, J., A Harnack inequality for parabolic differential equations, Comm. Pure Appl. Math., 17 (1964), p. 101–134.Google Scholar