Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T15:08:52.188Z Has data issue: false hasContentIssue false
  • English
  • Français

A prime decomposition symbol for a non-abelian central extension which is abelian over a bicyclic biquadratic field

Published online by Cambridge University Press:  22 January 2016

Yoshiomi Furuta
Yoshiomi Furuta*
Affiliation:
Kanazawa University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a previous paper [6] we had some criteria for the prime decomposition in certain non-abelian extensions over the rational number field Q, and as its special case we had a reciprocity of the biquadratic residue symbol. The reciprocity was obtained by using a descent method of the prime decomposition for a central extension over Q which is abelian over a biquadratic field 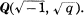In the present paper we study on the case over a biquadratic field 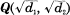in general. We define a symbol [d1, d2, p] which expresses the decomposition law of a rational prime p in a central extension mentioned above.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 79 , October 1980 , pp. 79 - 109
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1980

References

[ 1 ] Fröhlich, A., On fields of class two, Proc. London Math. Soc. (3), 4 (1954), 235–256.Google Scholar
[ 2 ] Fröhlich, A., A prime decomposition symbol for certain non Abelian number fields, Acta Sci. Math., 21 (1960), 229–246.Google Scholar
[ 3 ] Furuta, Y., A reciprocity law of the power residue symbol, J. Math. Soc. Japan, 10 (1958), 46–54.Google Scholar
[ 4 ] Furuta, Y., The genus field and genus number in algebraic number fields, Nagoya Math. J., 29 (1967), 281–285.Google Scholar
[ 5 ] Furuta, Y., On nilpotent factors of congruent ideal class groups of Galois extensions, Nagoya Math. J., 62 (1976), 13–28.Google Scholar
[ 6 ] Furuta, Y., Note on class number factors and prime decompositions, Nagoya Math. J., 66 (1977),167–182.Google Scholar
[ 7 ] Hasse, H., Normenresttheorie galoisscher Zahlkörper mit Anwendungen auf Führer und Diskriminante abelscher Zahlkorper, J. Fac. Sci. Tokyo Imp. Univ., 2 (1934), 477–498.Google Scholar
[ 8 ] Hasse, H., Zur Geschlechtertheorie in quadratischen Zahlkorper, J. Math. Soc. Japan, 3 (1951), 45–51.CrossRefGoogle Scholar
[ 9 ] Iyanaga, S., The theory of numbers, North Holland/American Elsevier (1975).Google Scholar
[10] Kaplan, P., Représentation de nombres premiers par des formes quadratiques binaires de discriminant —π, oú π≡1 mod. 4), C. R. Acad. Sc. Paris, 275 (1973), 1535–1537.Google Scholar
[11] Lehmer, E., On some special quartic reciprocity laws, Acta Arith., 21 (1972), 367–377.Google Scholar
[12] Redei, L., Ein neues zahlentheoretisches Symbol mit Anwendungen auf Theorie der quadratischen Zahlkorper, J. reine und angew. Math., 180 (1939), 1–43.Google Scholar
[13] Shirai, S., On the central class field mod. m of Galois extensions of an algebraic number field, Nagoya Math. J., 71 (1978), 61–85.Google Scholar