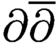Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T20:12:47.749Z Has data issue: false hasContentIssue false
  • English
  • Français

POWER SERIES PROOFS FOR LOCAL STABILITIES OF KÄHLER AND BALANCED STRUCTURES WITH MILD $\partial \overline {\partial }$-LEMMA

Part of: Global differential geometry Deformations of analytic structures Commutative algebra: Homological methods Families, fibrations

Published online by Cambridge University Press:  08 June 2021

SHENG RAO Open the ORCID record for SHENG RAO [Opens in a new window] ,
XUEYUAN WAN Open the ORCID record for XUEYUAN WAN [Opens in a new window]  and
QUANTING ZHAO Open the ORCID record for QUANTING ZHAO [Opens in a new window]
SHENG RAO
Affiliation:
School of Mathematics and statistics Wuhan UniversityWuhan430072China Department of Mathematics University of California at Los AngelesLos Angeles, [email protected]
XUEYUAN WAN
Affiliation:
Mathematical Science Research Center Chongqing University of [email protected]
QUANTING ZHAO
Affiliation:
School of Mathematics and Statistics & Hubei Key Laboratory of Mathematical Sciences Central China Normal UniversityWuhan430079P.R. [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

By use of a natural map introduced recently by the first and third authors from the space of pure-type complex differential forms on a complex manifold to the corresponding one on the small differentiable deformation of this manifold, we will give a power series proof for Kodaira–Spencer’s local stability theorem of Kähler structures. We also obtain two new local stability theorems, one of balanced structures on an n-dimensional balanced manifold with the 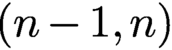$(n-1,n)$ th mild 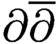$\partial \overline {\partial }$ -lemma by power series method and the other one on p-Kähler structures with the deformation invariance of 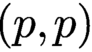$(p,p)$ -Bott–Chern numbers.

MSC classification

Primary: 32G05: Deformations of complex structures
Secondary: 13D10: Deformations and infinitesimal methods 14D15: Formal methods; deformations 53C55: Hermitian and Kählerian manifolds
Type
Article
Information
Nagoya Mathematical Journal , Volume 246 , June 2022 , pp. 305 - 354
Check for updates
Copyright
© (2021) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Rao is partially supported by the National Natural Science Foundations of China No. 11671305, 11771339, 11922115 and China Scholarship Council/University of California, Los Angeles Joint Scholarship Program.

†

Wan is partially supported by Scientific Research Foundation of Chongqing University of Technology.

‡

Zhao is partially supported by the National Natural Science Foundations of China No. 11801205.

References

Alessandrini, L., Proper modifications of generalized p-Kähler manifolds, J. Geom. Anal. 27 (2017), no. 2, 947–967.CrossRefGoogle Scholar
Alessandrini, L. and Andreatta, M., Closed transverse $\left(p,p\right)$ -forms on compact complex manifolds, Compos. Math. 61 (1987), no. 2, 181–200. Erratum 63 (1987), no. 1, 143.Google Scholar
Alessandrini, L. and Bassanelli, G., Small deformations of a class of compact non-Kähler manifolds, Proc. Amer. Math. Soc. 109 (1990), no. 4, 1059–1062.Google Scholar
Alessandrini, L. and Bassanelli, G., Compact $p$ -Kähler manifolds, Geom. Dedicata 38 (1991), 199–210.CrossRefGoogle Scholar
Alessandrini, L. and Bassanelli, G., Positive $\partial \overline{\partial}$ -closed currents and non-Kähler geometry, J. Geom. Anal. 2 (1992), 291–361.CrossRefGoogle Scholar
Angella, D., The cohomologies of the Iwasawa manifold and its small deformations, J. Geom. Anal. 23 (2013), no. 3, 1355–1378.CrossRefGoogle Scholar
Angella, D. and Kasuya, H., Bott–Chern cohomology of solvmanifolds, Ann. Glob. Anal. Geom. 52 (2017), no. 4, 363–411.CrossRefGoogle Scholar
Angella, D. and Tomassini, A., On the $\partial \overline{\partial}$ -lemma and Bott–Chern cohomology, Invent. Math. 192 (2013), no. 1, 71–81.CrossRefGoogle Scholar
Angella, D. and Ugarte, L., Locally conformal Hermitian metrics on complex non-Kähler manifolds, Mediterr. J. Math. 13 (2016), no. 4, 2105–2145.CrossRefGoogle Scholar
Angella, D. and Ugarte, L., On small deformations of balanced manifolds, Differ. Geom. Appl. 54 (2017), no. part B, 464–474.CrossRefGoogle Scholar
Barannikov, S. and Kontsevich, M., Frobenius manifolds and formality of Lie algebras of polyvector fields, Int. Math. Res. Not. (1998), no. 4, 201–215.CrossRefGoogle Scholar
Campana, F., The class $\mathbf{\mathcal{C}}$  is not stable by small deformation, Math. Ann. 290 (1991), 19–30.CrossRefGoogle Scholar
Clemens, H., Geometry of formal Kuranishi theory, Adv. Math. 198 (2005), 311–365.CrossRefGoogle Scholar
Console, F. and Fino, A., Dolbeault cohomology of compact nilmanifolds, Transform. Groups 6 (2001), no. 2, 111–124.CrossRefGoogle Scholar
Console, F., Fino, A., and Poon, Y.-S., Stability of abelian complex structures, Int. J. Math. 17 (2006), no. 4, 401–416.CrossRefGoogle Scholar
Cordero, L., Fernández, M., Gray, A., and Ugarte, L., Compact nilmanifolds with nilpotent complex structures: Dolbeault cohomology, Trans. Amer. Math. Soc. 352 (2000), 5405–5433.CrossRefGoogle Scholar
Deligne, P., Griffiths, P., Morgan, J., and Sullivan, D., Real homotopy theory of Kähler manifolds, Invent. Math. 29 (1975), 245–274.CrossRefGoogle Scholar
Demailly, J.-P., Complex analytic and differential geometry (2012), book online http://www-fourier.ujf-grenoble.fr/demailly/books.html.Google Scholar
Demailly, J.-P. and Paun, M., Numerical characterization of the Kähler cone of a compact Kähler manifold, Ann. Math. 159 (2004), 1247–1274.CrossRefGoogle Scholar
Douglis, A. and Nirenberg, L., Interior estimates for elliptic systems of partial differential equations, Comm. Pure Appl. Math. 8 (1955), 503–538.CrossRefGoogle Scholar
Friedman, R., “On threefolds with trivial canonical bundle”. in Complex geometry and Lie theory (Sundance, UT, 1989), Proc. Sympos. Pure Math., Vol. 53, Amer. Math. Soc., Providence, RI, 1991, 103–134.CrossRefGoogle Scholar
Fu, J., Li, J., and Yau, S.-T., Balanced metrics on non-Kähler Calabi–Yau threefolds, J. Differ. Geom. 20 (2012), 81–129.Google Scholar
Fu, J. and Yau, S.-T., A note on small deformations of balanced manifolds, C. R. Math. Acad. Sci. Paris 349 (2011), no. 13-14, 793–796.CrossRefGoogle Scholar
Griffiths, P. and Harris, J., Principles of Algebraic Geometry, Pure and Applied Mathematics. Wiley-Interscience [John Wiley & Sons], New York, NY, 1978.Google Scholar
Harvey, R., “Holomorphic chains and their boundaries”. Several complex variables (Proc. Sympos. Pure Math., Vol. XXX, Part 1, Williams Coll., Williamstown, MA., 1975). Amer. Math. Soc., Providence, RI, 1977, 309–382.CrossRefGoogle Scholar
Harvey, R. and Knapp, A., Positive (p,p)-forms, Wirtinger’s Inequality and Currents, Procs Tulane Univ. Program on Value Distribution Theory in Complex Analysis and Related Topics in Differential Geometry 1972-73, Dekker, New York, NY, 1974, 43–62.Google Scholar
Kasuya, H., Techniques of computations of Dolbeault cohomology of solvmanifolds, Math. Z. 273 (2013), no. 1-2, 437–447.CrossRefGoogle Scholar
Kodaira, K., Complex Manifolds and Deformations of Complex Structures, Grundlehren der Math. Wiss. 283, Springer, New York, NY, 1986.CrossRefGoogle Scholar
Kodaira, K. and Spencer, D., On deformations of complex analytic structures. III. Stability theorems for complex structures, Ann. Math. Sec. Ser. 71 (1960), 43–76.CrossRefGoogle Scholar
Krantz, S. and Parks, H., A Primer of Real Analytic Functions, 2nd ed., Birkhäuser Advanced Texts: Basler Lehrbücher. [Birkhäuser Advanced Texts: Basel Textbooks] Birkhäuser Boston, Inc., Boston, MA, 2002.CrossRefGoogle Scholar
Kuranishi, M., New proof for the existence of locally complete families of complex structures, Proc. Conf. Complex Analysis (Minneapolis, 1964). Springer, Berlin, Germany, 1965, 142–154.Google Scholar
Latorre, A., Ugarte, L., and Villacampa, R., On the Bott–Chern cohomology and balanced Hermitian nilmanifolds, Int. J. Math. 25 (2014), no. 6, 1450057, 24 pp.CrossRefGoogle Scholar
Lebrun, C. and Poon, Y.-S., Twisors, Kähler manifolds, and bimeromorphic geometry II, J. Amer. Math. Soc. 5 (1992), no. 2, 317–325.Google Scholar
Li, Y., On deformations of generalized complex structures: The generalized Calabi–Yau case, October 2005. arXiv:0508030v2.Google Scholar
Liu, K. and Rao, S., Remarks on the Cartan formula and its applications, Asian J. Math 16 (2012), no. 1, 157–170.CrossRefGoogle Scholar
Liu, K., Rao, S., and Yang, X., Quasi-isometry and deformations of Calabi–Yau manifolds, Invent. Math. 199 (2015), no. 2, 423–453.CrossRefGoogle Scholar
Liu, K., Sun, X., Yau, S.-T, “Recent development on the geometry of the Teichmüller and moduli spaces of Riemann surfaces”. Surveys in differential geometry. Geometry of Riemann surfaces and their moduli spaces, Surv. Differ. Geom., 14, Int. Press, Somerville, MA, 2009, 221–259.Google Scholar
Michelsohn, M., On the existence of special metrics in complex geometry, Acta Math. 149 (1982), 261–295.CrossRefGoogle Scholar
Morrow, J. and Kodaira, K., Complex manifolds, Holt, Rinehart and Winston, Inc., New York-Montreal, Que.-London, 1971.Google Scholar
Nakamura, I., Complex parallelisable manifolds and their small deformations, J. Differ. Geom. 10 (1975), 85–112.CrossRefGoogle Scholar
Popovici, D., Aeppli cohomology classes associated with Gauduchon metrics on compact complex manifolds, Bull. Soc. Math. France 143 (2015), no. 4, 763–800.CrossRefGoogle Scholar
Popovici, D. and Ugarte, L., Compact complex manifolds with small Gauduchon cone, Proc. London Math. Soc. (3) 116 (2018), no. 5, 1161–1186.CrossRefGoogle Scholar
Rao, S. and Zhao, Q., Several special complex structures and their deformation properties, J. Geom. Anal. 28 (2018), no. 4, 2984–3047.CrossRefGoogle Scholar
Rao, S., Wan, X., and Zhao, Q., On local stabilities of  $p$ -Kähler structures, Compos. Math. 155 (2019), no. 3, 455–483.CrossRefGoogle Scholar
Rollenske, S., Geometry of nilmanifolds with left-invariant complex structure and deformations in the large, Proc. London Math. Soc. 99 (2009), 425–460.CrossRefGoogle Scholar
Salamon, S., Complex structures on nilpotent Lie algebras, J. Pure Appl. Algebra 157 (2001), 311–333.CrossRefGoogle Scholar
Sullivan, D., Cycles for the dynamical study of foliated manifolds and complex manifolds, Invent. Math. 36 (1976), 225–255.CrossRefGoogle Scholar
Sun, X., Deformation of canonical metrics I, Asian J. Math. 16 (2012), no. 1, 141–155.CrossRefGoogle Scholar
Sun, X. and Yau, S.-T., Deformation of Kähler–Einstein metrics, Surveys in geometric analysis and relativity, Adv. Lect. Math. (ALM), 20, Int. Press, Somerville, MA, 2011, 467–489.Google Scholar
Tian, G., Smoothness of the universal deformation space of compact Calabi–Yau manifolds and its Petersson-Weil metric, Mathematical aspects of string theory (San Diego, Calif., 1986), Adv. Ser. Math. Phys., 1, World Sci. Publishing, Singapore, Asia, 1987, 629–646.CrossRefGoogle Scholar
Todorov, A., The Weil-Petersson geometry of the moduli space of  $\mathrm{SU}\left(n\ge 3\right)$ (Calabi–Yau) manifolds I, Comm. Math. Phys. 126 (1989), no. 2, 325–346.CrossRefGoogle Scholar
Ugarte, L. and Villacampa, R., Non-nilpotent complex geometry of nilmanifolds and heterotic supersymmetry, Asian J. Math. 18 (2014), no. 2, 229–246.CrossRefGoogle Scholar
Ugarte, L. and Villacampa, R., Balanced Hermitian geometry on  $6$ -dimensional nilmanifolds, Forum Math. 27 (2015), no. 2, 1025–1070.CrossRefGoogle Scholar
Voisin, C., Hodge Theory and Complex Algebraic Geometry. I, Translated from the French original by Leila Schneps. Cambridge Studies in Advanced Mathematics, 76. Cambridge University Press, Cambridge, MA, 2002.CrossRefGoogle Scholar
Wu, C.-C., On the geometry of superstrings with torsion, Ph.D. thesis, Harvard University, 2006, 60 pp.Google Scholar
Zhao, Q. and Rao, S., Applications of deformation formula of holomorphic one-forms, Pacific J. Math. 266 (2013), no. 1, 221–255.CrossRefGoogle Scholar
Zhao, Q. and Rao, S., Extension formulas and deformation invariance of Hodge numbers, C. R. Math. Acad. Sci. Paris 353 (2015), no. 11, 979–984.CrossRefGoogle Scholar