Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T23:26:19.492Z Has data issue: false hasContentIssue false
  • English
  • Français

Potential theoretic properties of the gradient of a convex function on a functional space

Published online by Cambridge University Press:  22 January 2016

Nobuyuki Kenmochi  and
Yoshihiro Mizuta
Nobuyuki Kenmochi
Affiliation:
Department of Mathematics, Faculty of Education Chiba University Chiba, Japan
Yoshihiro Mizuta
Affiliation:
Department of Mathematics, Faculty of Science, Hiroshima University Hiroshima, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the previous paper [11], introducing the notions of potentials and of capacity associated with a convex function Φ given on a regular functional space 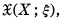we discussed potential theoretic properties of the gradient ∇Φ which were originally introduced and studied by Calvert [5] for a class of nonlinear monotone operators in Sobolev spaces. For example:

  • (i) The modulus contraction operates.

  • (ii) The principle of lower envelope holds.

  • (iii) The domination principle holds.

  • (iv) The contraction Tk onto the real interval [0, k] (k > 0) operates.

  • (v) The strong principle of lower envelope holds.

  • (vi) The complete maximum principle holds.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 59 , December 1975 , pp. 199 - 215
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1975

References

[1] Brezis, H. and Stampacchia, G., Sur la régularité de la solution d’inéquations elliptiques, Bull. Soc. Math. France 96 (1968), 153–180.Google Scholar
[2] browder, F. E., On a theorem of Beurling and Livingston, Canad. J. Math. 17 (1965), 367–372.CrossRefGoogle Scholar
[3] Browder, F. E., Nonlinear variational inequalities and maximal monotone mappings in Banach spaces, Math. Ann. 183 (1969), 213–231.Google Scholar
[4] Calvert, B., Nonlinear equations of evolution, Pacific J. Math. 39 (1971), 293–350.CrossRefGoogle Scholar
[5] Calvert, B., Potential theoretic properties for nonlinear monotone operators, Boll. Un. Mat. Ital. 5 (1972), 473–489.Google Scholar
[6] Crandall, M. G. and Liggett, T. M., Generation of semigroups of nonlinear transformations on general Banach spaces, Amer. J. Math. 93 (1971), 265–298.CrossRefGoogle Scholar
[7] Deny, J., Sur les espaces de Dirichlet, Sém. théorie du potentiel, Paris, 1957.Google Scholar
[8] Itô, M., A note on extended regular functional spaces, Proc. Japan Acad. 43 (1967), 435–440.Google Scholar
[9] Kato, T., Accretive operators and nonlinear evolution equations in Banach spaces, Proc. Symp. Pure Math. A. M. S. 18, Part 1 (1970), 138–161.CrossRefGoogle Scholar
[10] Kenmochi, N., Nonlinear operators of monotone type in reflexive Banach spaces and nonlinear perturbations, Hiroshima Math. J. 4 (1974), 229–263.Google Scholar
[11] Kenmochi, N. and Mizuta, Y., The gradient of a convex function on a regular functional space and its potential theoretic properties, Hiroshima Math. J. 4 (1974), 743–763.CrossRefGoogle Scholar
[12] Kōmura, Y., Nonlinear semigroups in Hilbert space, J. Math. Soc. Japan 19 (1967), 493–507.Google Scholar
[13] Konishi, Y., Nonlinear semigroups in Banach lattices, Proc. Japan Acad. 47 (1971), 24–28.Google Scholar