Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Segawa, Shigeo
1981.
A duality relation for harmonic dimensions and its applications.
Kodai Mathematical Journal,
Vol. 4,
Issue. 3,
Nakai, Mitsuru
and
Tada, Toshimasa
1982.
Dirichlet integral and Picard principle.
Nagoya Mathematical Journal,
Vol. 86,
Issue. ,
p.
85.
Kawamura, Michihiko
and
Segawa, Shigeo
1993.
P-harmonic dimensions on ends.
Nagoya Mathematical Journal,
Vol. 132,
Issue. ,
p.
131.


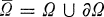 with nonnegative locally Hölder continuous coefficients
with nonnegative locally Hölder continuous coefficients 
