Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T23:38:35.811Z Has data issue: false hasContentIssue false
  • English
  • Français

The One-Dimensional Stratum in the Boundary of the Moduli Stack of Stable Curves

Published online by Cambridge University Press:  11 January 2016

Jörg Zintl
Jörg Zintl*
Affiliation:
Fachbereich Mathematik Technische Universität Kaiserslautern, Postfach 3049 67653 Kaiserslautern, Germany, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well-known that the moduli space 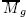of Deligne-Mumford stable curves of genus g admits a stratification by the loci of stable curves with a fixed number i of nodes, where 0 ≤ i ≤ 3g - 3. There is an analogous stratification of the associated moduli stack .

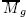Keywords

14H1014H37
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 196 , 2009 , pp. 27 - 66
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2009

References

[DM] Deligne, P. and Mumford, D., The irreducibility of the space of curves of a given genus, Publ. Math. I.H.E.S., 36 (1969), 75–109.Google Scholar
[E] Edidin, D., Notes on the construction of the moduli space of curves, Recent progress in intersection theory (G. Ellingsrud, et al., eds.), 2000, pp. 85–113.Google Scholar
[F] Faber, C., Chow rings of moduli spaces of curves I: The Chow ring of M3, Annals of Maths., 132 (1990), 331–419.Google Scholar
[G] Gieseker, D., Lectures on moduli of curves, Tata Institute Lecture Notes 69, 1982.Google Scholar
[HM] Harris, J. and Morrison, I., Moduli of Curves, Springer-Verlag, New York, 1998.Google Scholar
[K] Knudsen, F., The projectivity of the moduli space of stable curves, II: the stacks Mg,n , Math. Scand., 52 (1983), 161–199.Google Scholar
[Z1] Zintl, J., One-dimensional substacks of the moduli stack of Deligne-Mumford stable curves, Habilitationsschrift, Kaiserslautern, 2005, math. AG/0612802.Google Scholar
[Z2] Zintl, J., Moduli stacks of permutation classes of pointed stable curves, Milan j. math., 76 (2008), 401–418, math.AG/0611710.Google Scholar