Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T20:06:17.804Z Has data issue: false hasContentIssue false
  • English
  • Français

On vector bundles on algebraic surfaces and 0-cycles

Published online by Cambridge University Press:  22 January 2016

E. Ballico
E. Ballico*
Affiliation:
Department of Mathematics, University of Trento, 38050 Povo (TN), Italy
*
e-mail: (bitnet) ballico itncisca (Decnet) itnvaxi: ballico fax: italy + 461881624
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be an algebraic complex projective surface equipped with the euclidean topology and E a rank 2 topological vector bundle on X. It is a classical theorem of Wu ([Wu]) that E is uniquely determined by its topological Chern classes 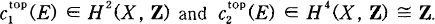. Viceversa, again a classical theorem of Wu ([Wu]) states that every pair (a, b) ∈ (H (X, Z), Z) arises as topological Chern classes of a rank 2 topological vector bundle. For these results the existence of an algebraic structure on X was not important; for instance it would have been sufficient to have on X a holomorphic structure. In [Sch] it was proved that for algebraic X any such topological vector bundle on X has a holomorphic structure (or, equivalently by GAGA an algebraic structure) if its determinant line bundle has a holomorphic structure. It came as a surprise when Elencwajg and Forster ([EF]) showed that sometimes this was not true if we do not assume that X has an algebraic structure but only a holomorphic one (even for some two dimensional tori (see also [BL], [BF], or [T])).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 130 , June 1993 , pp. 19 - 23
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1993

References

[BB] Ballico, E., Brussee, R., On the unbalance of vector bundles on a blow-up surface, preprint (1990).Google Scholar
[BL] Banica, C. and Potier, J. Le, Sur l’existence des fibres vectoriels holomorphes sur les surfaces, J. reine angew. Math., 378 (1987), 1–31.Google Scholar
[B] Bloch, S., Lectures on algebraic cycles, Duke Univ. Math. Series, 1980.Google Scholar
[Br] Brun, J., Let fibres de rang deux sur P et leur sections, Bull. Soc. Math. France, 107(1979), 457–473.Google Scholar
[BF] Brinzanescu, V. and Flonder, P., Holomorphic 2-vector bundles on nonalgebraic 2-tori, J. reine angew. Math., 363 (1985), 47–58.Google Scholar
[C] Catanese, F., Footnotes to a theorem of Reider, in: Algebraic Geometry Proceedings, L’Aquila 1988 (ed. by Sommese, A. J., Biancofiore, A., Livorni, E. L.), pp. 67–74. Lecture Notes in Math., 1417, Springer-Verlag 1990.Google Scholar
[EF] Elencwajg, G. and Forster, O., Vector bundles on manifolds without divisors and a theorem on deformations, Ann. Inst. Fourier, 32 (1983), 25–51.CrossRefGoogle Scholar
[Fu] Fulton, W., Intersecation theory, Ergeb. der Math., 2, Springer-Verlag, 1984.CrossRefGoogle Scholar
[Li] Lieberman, D., Intermediate Jacobians, in: Algebraic Geometry, Oslo 1970, pp. 125–139, Wolters-Noordhoff Publ., 1972.Google Scholar
[Mu] Mumford, D., Rational equivalence of 0-cycles on surfaces, J. Math. Kyoto Univ., 9 (1969), 195–204.Google Scholar
[Sa] Samuel, P., Relations d’équivalence en géométrie algébrique, Proc. Intern. Cong. Math, Edinburgh 1958, pp. 470–487.Google Scholar
[Sch] Schwarzenberger, R. L. E., Vector bundles on algebraic surfaces, Proc. London Math. Soc, (3) 11 (1961), 601–622.Google Scholar
[T] Toma, M., Une classe de fibres vectoriels holomorphes sur les 2-tore complexe, C. R. Acad. Sci. Paris, 311 (1990), Serie I, 257–258.Google Scholar
[Wu] Wen-tsien, Wu, Sur les espaces fibres, Publ. Inst. Univ. Strasbourg, 11, Paris, 1952.Google Scholar