Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T23:00:27.276Z Has data issue: false hasContentIssue false
  • English
  • Français

On Transitive Simple Groups of Degree 3p*)

Published online by Cambridge University Press:  22 January 2016

Noboru Ito
Noboru Ito*
Affiliation:
Department of Mathematics, Cornell University, Ithaca, New York, U.S.A. and Mathematical Institute, Nagoya University, Nagoya-Chikusa, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Q be the set of symbols 1, 2,…, 3 p, where p is an prime number greater than 3. Let 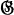be a transitive permutation group on Ω, which is simple and in which the normalizer of a Sylow p-subgroup has order 2 p.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 21 , December 1962 , pp. 123 - 158
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1962

Footnotes

*)

This work was supported by the United States Army under Contract No. DA-ARO(D)-31-124-G 86 monitored by the Army Research Office.

References

[1] Bochert, A., Ueber die Classe der transitiven Substitutionengruppen, Math. Annalen 40 (1892), pp. 176–193.Google Scholar
[2] Bochert, A., Ueber die Classe der transitiven Substitutionengruppen II, Math. Annalen 49 (1897), pp. 134–144.Google Scholar
[3] Brauer, R., On permutation groups of prime degree and related classes of groups, Ann. of Math. 44 (1943), pp. 57–79.Google Scholar
[4] Brauer, R., On the structure of groups of finite order, Proceedings of the International Congress of Mathematicians, Amsterdam (1954).Google Scholar
[5] Brauer, R., Number theoretical investigations on groups of finite order, Proceedings of the International Symposium on Algebraic Number Theory, Tokyo-Nikko (1955).Google Scholar
[6] Brauer, R. and Feit, W., On the number of irreducible characters of finite groups in a given block, Proc. Nat. Acad. Sci. U.S.A. 45 (1959), pp. 361–365.Google Scholar
[7] Brauer, R. and Fowler, K., On groups of even order, Ann. of Math. 62 (1955), pp. 565–583.Google Scholar
[8] Brauer, R. and Nesbitt, C., On the modular characters of groups, Ann. of Math. 42 (1941), pp. 556–590.Google Scholar
[9] Brauer, R. and Suzuki, M., On finite groups whose 2-Sylow group is a generalized quaternion group, Proc. Nat. Acad. Sci. U.S.A. 45 (1959), pp. 1757-1759.Google Scholar
[10] Brauer, R. and Tuan, H., On simple groups of finite order. I, Bull, of Amer. Math. Soc., 51 (1945), pp. 756–766.Google Scholar
[11] Carmichael, R., Introduction to the theory of groups of finite order, Boston (1937).Google Scholar
[12] Frobenius, G., Ueber die Charaktere der symmetrischen Gruppe, Sitzungsber. der Preuss. Akad. der Wiss. (1900), pp. 516–534.Google Scholar
[13] Gorenstein, D. and Walter, J., On finite groups with dihedral Sylow 2-subgroups, to appear.Google Scholar
[14] Ito, N., Zur Theorie der Permutationsgruppen vom Grad p , Math. Zeitschr. 74 (1960), pp. 299–301.Google Scholar
[15] Ito, N., On transitive simple groups of degree 2 p , Math. Zeitschr. 78 (1962), pp. 453–468.Google Scholar
[16] Suzuki, M., A characterization of simple groups LF(2, p), J. Fac. Sci. Univ. Tokyo. Sect. I, 6 (1951), pp. 259–293.Google Scholar
[17] Suzuki, M., Applications of group characters, Proceedings of Symposia in Pure Mathematics, 1, American Mathematical Society, (1959), pp. 88–99.Google Scholar
[18] Thompson, John wrote to the author that he does not intend to publish this “special” result, but he and Feit, Walter are preparing, to publish a proof of the full Burnside conjecture.Google Scholar
[19] Turkin, W., Kriterium der Einfachbeit einer endlichen Gruppe, Math. Annalen, 111 (1935), pp. 281–284.Google Scholar
[20] Tsuzuku, T., On multiple transitivity of permutation groups, Nagoya Math. J. 18 (1961), pp. 93–109.Google Scholar
[21] Wielandt, H., Primitive Permutationsgruppen vom Grad 2 p , Math. Zeitschr. 63 (1956), pp. 478–485.Google Scholar
[22] Wielandt, H., Vorlesungen über Permutationsgruppen. Ausarbeitung von J. André, Tubingen, (1955).Google Scholar
[23] Wielandt, H., Beziehungen zwischen den Fixpunktzahlen von Automorphismengruppen einer endlichen Gruppe, Math. Zeitschr. 73 (1960), pp. 146–158.Google Scholar
[24] Zassenhaus, H., Kennzeichnung endlicher linearer Gruppen als Permutationsgruppen, Abh. Math. Sem. Univ. Hamburg 11, 17–40 (1935).Google Scholar