Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T22:58:44.416Z Has data issue: false hasContentIssue false
  • English
  • Français

On Theta Functions and Abelian Varieties over Valuation Fields of Rank One: (II) Theta Functions and Abelian Functions of Characteristic p(>0)

Published online by Cambridge University Press:  22 January 2016

Hisasi Morikawa
Hisasi Morikawa*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It may safely said that one of the most important problems in modern algebraic geometry is to elevate theory of abelian functions to the same level as theory of elliptic functions beyond the modern formulation of classical results. Being concerned in such a problem, we feel that one of the serious points is the lack of knowladge on the explicit expressions of abelian varieties and their law of compositions by means of their canonical systems of coordinates: Such expressions correspond to the cubic relation 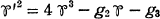of Weierstrass’ 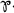-functions and their addition formulae in theory of elliptic functions.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 21 , December 1962 , pp. 231 - 250
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1962

References

[1] Baker, H. F., Abel’s theorem and the applies theory, Cambridge 1897.CrossRefGoogle Scholar
[2] Morikawa, H., On theta functions and abelian varieties over valuation fields of rank one (I), Nagoya Math. Jour. Vol. 20, June. (1962), p. 1–27.CrossRefGoogle Scholar