Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kurita, Minoru
1961.
Tensor Fields and Their Parallelism.
Nagoya Mathematical Journal,
Vol. 18,
Issue. ,
p.
133.
Teufel, Eberhard
1982.
Differential topology and the computation of total absolute curvature.
Mathematische Annalen,
Vol. 258,
Issue. 4,
p.
471.


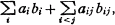 where
where 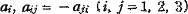 are quantities attached to
are quantities attached to 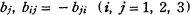 are quantities determined by our motion.
are quantities determined by our motion.