Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T07:44:02.871Z Has data issue: false hasContentIssue false
  • English
  • Français

On the unramified common divisor of discriminants of integers in a normal extension

Published online by Cambridge University Press:  22 January 2016

Satomi Oka
Satomi Oka*
Affiliation:
Department of Mathematics, Meijo University, Shiogamaguchi 1-501, Tenpakuku, Nagoya, 468-8502, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F be an algebraic number field of a finite degree, and K be a normal extension over F of a finite degree n. Let 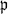be a prime ideal of F which is unramified in K/F, 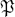be a prime ideal of K dividing 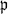such that 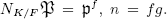. Denote by δ(K/F) the greatest common divisor of discriminants of integers of K with respect to K/F. Then, 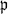divides δ(K/F) if and only if

Keywords

Primary:11R04Secondary:11R29
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 160 , 2000 , pp. 181 - 186
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2000

References

[1] Dedekind, R., Über den Zusammenhang zwuschen der Theorie der Ideale und der Theorie der höheren Kongruenzen, Abh.der König. Gesell. der Wiss. zu Göttingen, 23 (1878), 1–23, Complete works, Chelsea, 1969.Google Scholar
[2] Lang, S., Algebraic number theory, Addison-Wesley, 1970.Google Scholar
[3] Weiss, E., Algebraic number theory, AcGraw-Hill, 1963.Google Scholar