Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T05:14:34.506Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Theory of Differential Forms on Algebraic Varieties

Published online by Cambridge University Press:  22 January 2016

Yûsaku Kawahara
Yûsaku Kawahara*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be a function field of one variable over a perfect field k and let v be a valuation of K over k. Then 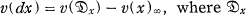is the different-divisor (Verzweigungsdivisor) of K/k(x), and (x)∞ is the denominator-divisor (Nennerdivisor) of x. In §1 we consider a generalization of this theorem in the function fields of many variables under some conditions. In §2 and §3 we consider the differential forms of the first kind on algebraic varieties, or the differential forms which are finite at every simple point of normal varieties and subadjoint hypersurfaces which are developed by Clebsch and Picard in the classical case. In §4 we give a proof of the following theorem. Let Vr be a normal projective variety defined over a field k of characteristic 0, and let ω1, …, ωs be linearly independent simple closed differential forms which are finite at every simple point of Vr. Then the induced forms on a generic hyperplane section are also linearly independent.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 11 , February 1957 , pp. 13 - 39
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1957

References

[1] Chevalley, C., On the theory of local rings, Annals of Math., vol. 44 (1943).Google Scholar
[2] Gorenstein, D., An arithmetic theory of adjoint plane curves, Trans. Amer. Math. Soc. 72 (1952).CrossRefGoogle Scholar
[3] Hecke, E., Vorlesungen über die Theorie der algebraischen Zahlen, (1923).Google Scholar
[4] Igusa, J., On the Picard varieties attached to algebraic varieties, Amer. J. Math. 74 (1952).Google Scholar
[5] Jung, H. W. E., Primteiler algebraischer Funktionen zweier unabhängigen Veränderlichen, Pal. Rend, vol. 26 (1908).Google Scholar
[6] Koizumi, S., On the differential forms of the first kind on algebraic varieties, Journ. Math. Soc. of Japan, vol. 1 (1949).Google Scholar
[7] Nakai, Y., On the divisors of differential forms on algebraic varieties, Journ. Math. Soc. of Japan, vol. 5 (1953).Google Scholar
[8] Nakai, Y., Some results in the theory of the differential forms of the first kind on algebraic varieties, Proc. Int. Symp. on Alg. Number Theory, (1956).Google Scholar
[9] Seidenberg, A., The hyperplane sections of normal varieties, Trans. Amer. Math. Soc. 69 (1950).Google Scholar
[10] Severi, F., Sugl’integrali algebrici semplici e doppi, Rend, della R. Acc. dei Lincei, s. VI, vol. VII (1928).Google Scholar
[11] Weil, A., Foundations of Algebraic Geometry, (1946).Google Scholar
[12] Weissinger, J., Zur arithmetische Theorie separierbarer Funktionenkörper, Abh. Math. Sem. Univ. Hamburg, vol. 16 (1948).Google Scholar