Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T23:03:11.460Z Has data issue: false hasContentIssue false
  • English
  • Français

On the structure of local cohomology modules for monomial curves in

Published online by Cambridge University Press:  22 January 2016

H. Bresinsky ,
F. Curtis ,
M. Fiorentini  and
L. T. Hoa
H. Bresinsky
Affiliation:
414 and 336 Neville Hall, University of Maine, Orono, Maine 04469-5752, U.S.A.
F. Curtis
Affiliation:
414 and 336 Neville Hall, University of Maine, Orono, Maine 04469-5752, U.S.A.
M. Fiorentini
Affiliation:
Dipartimento di Matematica, Universita di Ferrara, Via Machiavelli 35, Ferrara 44100, Italy
L. T. Hoa
Affiliation:
Institute of Mathematics, P. O. Box 631, Bo ho, Hanoi (Vietnam)
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our setting for this paper is projective 3-space over an algebraically closed field K. By a curve C ⊂ is meant a 1-dimensional, equidimensional projective algebraic set, which is locally Cohen-Macaulay. Let 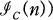be the Hartshorne-Rao module of finite length (cf. [R]). Here Z is the set of integers and ℐc the ideal sheaf of C. In [GMV] it is shown that , where is the homogeneous ideal of C, is the first local cohomology module of the R-module M with respect to . Thus there exists a smallest nonnegative integer k ∊ N such that , (see also the discussion on the 1-st local cohomology module in [GW]). Also in [GMV] it is shown that k = 0 if and only if C is arithmetically Cohen-Macaulay and C is arithmetically Buchsbaum if and only if k ≤ 1. We therefore have the following natural definition.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 136 , December 1994 , pp. 81 - 114
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1994

References

[B1] Bresinsky, H., Monomial Buchsbaum ideals in Pr , manuscripta Math., 47 (1984), 105–132.Google Scholar
[B2] Bresinsky, H., Minimal free resolutions of monomial curves in , Linear Alg. and Appl., 59 (1984), 121–129.Google Scholar
[BH] Bresinsky, H. and Huneke, C., Liaison of monomial curves in P 3 , J. reine angew. Math., 365 (1986), 33–66.Google Scholar
[BR] Bresinsky, H. and Renschuch, B., Basisbestimmung Veronesescher Projektions-ideale mit allgemeiner Nullstelle , Math. Nachr., 96 (1980), 257–269.Google Scholar
[BSV] Bresinsky, H., Schenzel, P. and Vogel, W., On liaison, arithmetically Buchsbaum curves and monomial curves in P 3 , J. Algebra, 86 (1984), 283 — 301.CrossRefGoogle Scholar
[BSS] Bresinsky, H., Schäfer, U. and Schenzel, P., On the canonical module for monomial curves, Comm. in Algebra, 15 (1987), 1799-1814.CrossRefGoogle Scholar
[EG] Eisenbud, D. and Goto, S., Linear free resolutions and minimal multiplicity, J. Algebra, 88 (1984), 89–133.Google Scholar
[FH] Fiorentini, M. and Hoa, L. T., On monomial k-Buchsbaum curves in Pn , Ann. Univ. Ferrara, Sez. VII, Sci. Mat, 36 (1990), 159–174.Google Scholar
[FV] Fiorentini, M. and Vogel, W., Old and new results and problems on Buchsbaum rings, I. Seminari di Geometria 1988–1991, pp. 53–61 Univ. Bologna 1991.Google Scholar
[GMV] Geramita, A. V., Maroscia, P. and Vogel, W., A note on arithmetically Buchsbaum curves in P3 , Matematiche (Catania), 40 (1985), 21–28.Google Scholar
[GW] Geramita, A. V. and Weibel, C. A., On the Cohen-Macaulay and Buchsbaum property for unions of planes in A n+1(k), J. Algebra, 92 (1985), 413–445.Google Scholar
[H] Hoa, L. T., On monomial k-Buchsbaum curves in P3 , Manuscripta Math., 73 (1991), 423–436.CrossRefGoogle Scholar
[HV] Hoa, L. T. and Vogel, W., Castelnuovo-Mumford regularity and hyperplane sections, J. Algebra (to appear).Google Scholar
[K] Kastner, J., Zu einem Problem von H. Bresinsky über monomiale Buchsbaum Kurven, Manuscripta Math., 54 (1985), 197–204.Google Scholar
[MM] Migliore, J. C. and Miro-Roig, R. M., On k-Buchsbaum curves in P 3 , Comm. in Algebra, 18 (1990), 2403–2422.Google Scholar
[Mo] Morales, M., Courbes monomiales dans l’espace projectif, module de Rao et liaison, Preprint Institute Fourier (Grenoble) 1993.Google Scholar
[M] Mumford, D., Lectures on curves on an algebraic surface, Ann. of Math. Studies 59, Princeton Univ. Press., Princeton, N. J., 1966.Google Scholar
[R] Rao, A. P., Liaison among curves in , Invent. Math., 50 (1979), 205–217.Google Scholar
[Ro] Rödseth, O. J., On a linear diophantine problem of Frobenius, J. reine angew Math., 301 (1978), 171–178.Google Scholar
[SV] Stückrad, J. and Vogel, W., Buchsbaum rings and applications, Springer Verlag 1986.Google Scholar
[TH] Trung, N. V. and Hoa, L. T., Affine semigroups and Cohen-Macaulay rings generated by monomials, Trans. Amer. Math. Soc., 298 (1986), 145–167.Google Scholar