Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T23:58:28.068Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Strong Unimodality of Lévy Processes

Published online by Cambridge University Press:  22 January 2016

Toshiro Watanabe
Toshiro Watanabe*
Affiliation:
Nakamandokoro, Aizubangemachi, Fukushima-ken, 969-65, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A measure μ(dx) on R is said to be unimodal with mode a if μ(dx) = cδa(dx) + f(x) dx, where c ≧ 0, δa(dx) is the delta measure at a and f(x) is non-decreasing for x < a and non-increasing for x > a. A measure 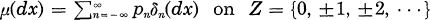is said to be unimodal with mode a if pn is non-decreasing for n ≦ a and non-increasing for n ≧ a. A probability measure μ(dx) on R (resp. on Z) is said to be strongly unimodal on R (resp. on Z) if, for every unimodal probability measure η(dx) on R (resp. on Z), the convolution μ*η(dx) is unimodal on R (resp. on Z).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 121 , March 1991 , pp. 195 - 199
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1991

References

[1] Ibragimov, I. A., On the composition of unimodal distributions, Theor. Probability Appl., 1 (1956), 255–260.Google Scholar
[2] Keilson, J. and Gerber, H., Some results for discrete unimodality, J. Amer. Statist. Assoc, 66 (1971), 386–389.Google Scholar
[3] Medgyessy, P., On a new class of unimodal infinitely divisible distribution functions and related topics, Studia Sci. Math. Hungar., 2 (1967), 441–446.Google Scholar
[4] Steutel, F. W. and van Harn, K., Discrete analogues of self-decomposability and stability, Ann. Probability, 7 (1979), 893–899.CrossRefGoogle Scholar
[5] Watanabe, T., Non-symmetric unimodal Levy processes that are not of class L, Japan. J. Math., 15 (1989), 191–203.Google Scholar
[6] Watanabe, T., On unimodal Levy processes on the nonnegative integers, Preprint.Google Scholar
[7] Wolfe, S. J., On the unimodality of infinitely divisible distribution functions, Z. Wahrsch. Verw. Gebiete, 45 (1978), 329–335.CrossRefGoogle Scholar
[8] Yamazato, M., Unimodality of infinitely divisible distribution functions of class L, Ann. Probability, 6 (1978), 523–531.CrossRefGoogle Scholar
[9] Yamazato, M., On strongly unimodal infinitely divisible distributions, Ann. Probability, 10 (1982), 589–601.CrossRefGoogle Scholar