Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T07:28:46.714Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Steinitz module and capitulation of ideals

Published online by Cambridge University Press:  22 January 2016

Chandrashekhar Khare  and
Dipendra Prasad
Chandrashekhar Khare
Affiliation:
Tata Institute of Fundamental Research, Colaba, Bombay-400005, [email protected]
Dipendra Prasad
Affiliation:
Tata Institute of Fundamental Research, Colaba, Bombay-400005, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let L be a finite extension of a number field K with ring of integers 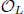and 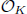respectively. One can consider 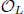as a projective module over 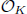. The highest exterior power of 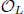as an 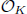module gives an element of the class group of 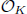, called the Steinitz module. These considerations work also for algebraic curves where we prove that for a finite unramified cover Y of an algebraic curve X, the Steinitz module as an element of the Picard group of X is the sum of the line bundles on X which become trivial when pulled back to Y. We give some examples to show that this kind of result is not true for number fields. We also make some remarks on the capitulation problem for both number field and function fields. (An ideal in 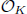is said to capitulate in L if its extension to 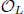is a principal ideal.)

Keywords

11R3711R2912A3516A26
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 160 , 2000 , pp. 1 - 15
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2000

References

[CR] Cornell, G. and Rosen, M., Cohomological analysis of class group extension problem, Queen’s papers in pure and applied Mathematics edited by Ribenboim, P., 54 (1979), 287–308.Google Scholar
[H] Hartshorne, R., Algebraic Geometry, Graduate texts in Mathematics, Springer-Verlag.Google Scholar
[FST] Frohlich, A., Serre, J-P. and Tate, J., A different with an odd class, J. de Crelle, 209 (1962), 6–7.Google Scholar
[I] Iwasawa, K., A note on the group of units in an algebraic number fields, J. Math. Pures Applied, 35 (1956), 189–192.Google Scholar
[M] Marcus, D.A., Number Fields, Universitext, Springer-Verlag.Google Scholar
[HS] Heider, F-P. and Schmithals, B., Zur Kapitulation der Idealklassen in unverzweigten primzyklischen Erweiterungen, J. Reine Agnew. Math., 336 (1982), 1–25.Google Scholar
[K] Kisilevsky, H., Olga Tausky-Todd’s work in Class field theory, Pacific J. of Mathematics, Olga Taussky-Todd memorial issue (1997), 219–224.CrossRefGoogle Scholar
[Mi] Miyake, K., Algebraic investigations of Hilbert’s theorem 94, the principal ideal theorem, and the capitulation problem, Expositiones Mathematicae, 7 (1989), 289–346.Google Scholar
[Na] Narkiewicz, W., Elementary and Analytic theory of algebraic numbers, 2nd edition, Springer-Verlag, PWN-Polish scientific publishers.Google Scholar
[Su] Suzuki, H., A generalization of Hilbert’s theorem 94, Nagoya Math. J., 121 (1991), 161–169.CrossRefGoogle Scholar