Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-22T17:11:44.844Z Has data issue: false hasContentIssue false
  • English
  • Français

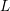ON THE STANDARD TWIST OF THE $L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS

Part of: Zeta and $L$-functions: analytic theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  26 December 2018

JERZY KACZOROWSKI  and
ALBERTO PERELLI
JERZY KACZOROWSKI
Affiliation:
Faculty of Mathematics and Computer Science, A.Mickiewicz University, 61-614 Poznań, Poland Institute of Mathematics of the Polish Academy of Sciences, 00-956 Warsaw, Poland email [email protected]
ALBERTO PERELLI
Affiliation:
Dipartimento di Matematica, Università di Genova, via Dodecaneso 35, 16146 Genova, Italy email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The standard twist 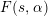$F(s,\unicode[STIX]{x1D6FC})$ of 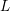$L$-functions 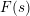$F(s)$ in the Selberg class has several interesting properties and plays a central role in the Selberg class theory. It is therefore natural to study its finer analytic properties, for example the functional equation. Here we deal with a special case, where 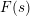$F(s)$ satisfies a functional equation with the same 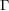$\unicode[STIX]{x1D6E4}$-factor of the 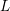$L$-functions associated with the cusp forms of half-integral weight; for simplicity we present our results directly for such 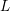$L$-functions. We show that the standard twist 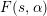$F(s,\unicode[STIX]{x1D6FC})$ satisfies a functional equation reflecting $s$ to 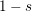$1-s$, whose shape is not far from a Riemann-type functional equation of degree 2 and may be regarded as a degree 2 analog of the Hurwitz–Lerch functional equation. We also deduce some results on the growth on vertical strips and on the distribution of zeros of 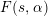$F(s,\unicode[STIX]{x1D6FC})$.

MSC classification

Primary: 11M41: Other Dirichlet series and zeta functions 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations 11F37: Forms of half-integer weight; nonholomorphic modular forms
Type
Article
Information
Nagoya Mathematical Journal , Volume 240 , December 2020 , pp. 150 - 180
Check for updates
Copyright
© 2018 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berndt, B. C., Two new proofs of Lerch’s functional equation, Proc. Amer. Math. Soc. 32 (1972), 403–408.Google Scholar
Bruinier, J. H., Modulformen halbganzen Gewichts und Beziehung zu Dirichletreihen, Diplomarbeit, Universität Heidelberg, 1997 (http://www.mathematik.tu-darmstadt.de/fbereiche/AlgGeoFA/staff/bruinier/publications/dipl.pdf).Google Scholar
Carletti, E., Monti Bragadin, G. and Perelli, A., A note on Hecke’s functional equation and the Selberg class, Funct. Approx. 41 (2009), 211–220.10.7169/facm/1261157810Google Scholar
Conrey, J. B. and Ghosh, A., On the Selberg class of Dirichlet series: small degrees, Duke Math. J. 72 (1993), 673–693.10.1215/S0012-7094-93-07225-0Google Scholar
Iwaniec, H., Topics in Classical Automorphic Forms, AMS Publications, 1997.10.1090/gsm/017Google Scholar
Kaczorowski, J., Some remarks on Fourier coefficients of Hecke modular functions, Comment. Math. (2004), 105–121; special volume in honorem J. Musielk.Google Scholar
Kaczorowski, J., “Axiomatic theory of L-functions: the Selberg class”, in Analytic Number Theory, Springer Lecture Notes in Mathematics 1891, (eds. Perelli, A. and Viola, C.) C.I.M.E. Summer School, Cetraro (Italy), 2006, 133–209.10.1007/978-3-540-36364-4_4Google Scholar
Kaczorowski, J., Molteni, G., Perelli, A., Steuding, J. and Wolfart, J., Hecke’s theory and the Selberg class, Funct. Approx. 35 (2006), 183–193.10.7169/facm/1229442622Google Scholar
Kaczorowski, J. and Perelli, A., On the structure of the Selberg class, I: 0⩽d⩽1, Acta Math. 182 (1999), 207–241.10.1007/BF02392574Google Scholar
Kaczorowski, J. and Perelli, A., “The Selberg class: a survey”, in Number Theory in Progress, Proc. Conf. in Honor of A. Schinzel, (eds. Györy, K. et al. ) de Gruyter, 1999, 953–992.Google Scholar
Kaczorowski, J. and Perelli, A., On the structure of the Selberg class, VI: non-linear twists, Acta Arith. 116 (2005), 315–341.10.4064/aa116-4-2Google Scholar
Kaczorowski, J. and Perelli, A., On the structure of the Selberg class, VII: 1 < d < 2, Ann. of Math. (2) 173 (2011), 1397–1441.10.4007/annals.2011.173.3.4Google Scholar
Kaczorowski, J. and Perelli, A., “Internal twists of L-functions”, in Number Theory, Analysis, and Combinatorics, (eds. Pintz, J. et al. ) de Gruyter, 2014, 145–154.Google Scholar
Kaczorowski, J. and Perelli, A., Twists and resonance of L-functions, I, J. Eur. Math. Soc. (JEMS) 18 (2016), 1349–1389.10.4171/JEMS/616Google Scholar
Kaczorowski, J. and Perelli, A., Some remarks on the convergence of the Dirichlet series of L-functions and related questions, Math. Z. 285 (2017), 1345–1355.10.1007/s00209-016-1750-6Google Scholar
Kaczorowski, J. and Perelli, A., A note on Linnik’s approach to the Dirichlet L-functions, Tr. Mat. Inst. Steklova 296 (2017), 123–132; (Russian); English transl. Proc. Steklov Inst. Math. 296 (2017), 115–124.Google Scholar
Kaczorowski, J. and Perelli, A., Introduction to the Selberg Class of $L$-Functions, in preparation.Google Scholar
Miyake, T., Modular Forms, Springer, 1989.10.1007/3-540-29593-3Google Scholar
Ogg, A., Modular Forms and Dirichlet Series, Benjamin, 1969.Google Scholar
Paris, R. B. and Kaminski, D., Asymptotics and Mellin–Barnes Integrals, Cambridge University Press, 2001.10.1017/CBO9780511546662Google Scholar
Perelli, A., A survey of the Selberg class of L-functions, part I, Milan J. Math. 73 (2005), 19–52.10.1007/s00032-005-0037-xGoogle Scholar
Perelli, A., A survey of the Selberg class of L-functions, part II, Riv. Mat. Univ. Parma (7) 3* (2004), 83–118.Google Scholar
Perelli, A., Non-linear twists of L-functions: a survey, Milan J. Math. 78 (2010), 117–134.10.1007/s00032-010-0119-2Google Scholar
Perelli, A., Converse theorems: from the Riemann zeta function to the Selberg class, Boll. Unione Mat. Ital. 10 (2017), 29–53.10.1007/s40574-016-0085-xGoogle Scholar
Selberg, A., “Old and new conjectures and results about a class of Dirichlet series”, in Proc. Amalfi Conf. Analytic Number Theory, Università di Salerno 1992; Collected Papers, vol. II, (eds. Bombieri, E. et al. ) Springer, 1991, 47–63.Google Scholar
Titchmarsh, E. C., The Theory of Functions, 2nd ed., Oxford University Press, 1939.Google Scholar