Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kanda, Mamoru
1970.
On the Singularity of Green Functions in Markov Processes II.
Nagoya Mathematical Journal,
Vol. 37,
Issue. ,
p.
209.
Kanda, Mamoru
1970.
Local comparison theorems for a certain class of multi-dimensional Markov processes of transient type.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 46,
Issue. 7.S1,
KANDA, Mamoru
1970.
Local Comparison Theorems for a Certain Class of Multi-Dimensional Markov Processes of Transient Type.
Proceedings of the Japan Academy,
Vol. 46,
Issue. 7Supplement,
p.
789.
Kanda, Mamoru
1971.
Comparison Theorems on Regular Points for Multidimensional Markov Processes of Transient Type.
Nagoya Mathematical Journal,
Vol. 44,
Issue. ,
p.
165.


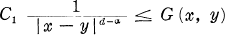
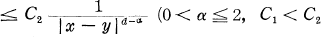 are positive constants), and showed that the regular points of its process are the same as those of
are positive constants), and showed that the regular points of its process are the same as those of 