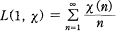Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Leu, Ming-Guang
2001.
Character sums and the series L(1, χ).
Journal of the Australian Mathematical Society,
Vol. 70,
Issue. 3,
p.
425.