Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T23:51:06.541Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Quadratic Extensions and the Extended Witt Ring of a Commutative Ring

Published online by Cambridge University Press:  22 January 2016

Teruo Kanzaki
Teruo Kanzaki*
Affiliation:
Osaka City University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let B be a ring and A a subring of B with the common identity element 1. If the residue A-module B/A is inversible as an A-A- bimodule, i.e. B/A ⊗A HomA(B/A, A) ≈ HomA(B/A, A) ⊗A B/A ≈ A, then B is called a quadratic extension of A. In the case where B and A are division rings, this definition coincides with in P. M. Cohn [2]. We can see easily that if B is a Galois extension of A with the Galois group G of order 2, in the sense of [3], and if 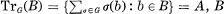is a quadratic extension of A. A generalized crossed product Δ(f, A, Φ, G) of a ring A and a group G of order 2, in [4], is also a quadratic extension of A.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 49 , March 1973 , pp. 127 - 141
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1973

References

[1] Bass, H.: Lecture on Topics in Algebraic K-theory, Tata Institute of Fundamental Research, Bombay, 1967.Google Scholar
[2] Cohn, P. M.: Quadratic extensions of skew fields, Proc. London Math. Soc. 11 (1961) 531–556.Google Scholar
[3] Kanzaki, T.: On commutor ring and Galois theory of separable algebras, Osaka J. Math. 1 (1964).Google Scholar
[4] Kanzaki, T.: Generalized crossed product and Brauer group, Osaka J. Math. 5 (1968) 175–188.Google Scholar
[5] Kanzaki, T.: On bilinear module and Witt ring over a commutative ring, Osaka J. Math. 8 (1971) 485–496.Google Scholar
[6] Micali, P. A. and Villamayor, O. E.: Algebra de Clifford et groupe de Brauer, Ann. scient. Ec. Norm. Sup., t. 4 (1971) 285–310.Google Scholar
[7] Revoy, P. P.: Sur les deux premiers invariants d’une forme quadratique, Ann. scient. Ec. Norm. Sup., t. 4 (1971) 311–319.Google Scholar