Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Miyata, Yoshimasa
1980.
On the module structure of a p-extension over a -adic number field.
Nagoya Mathematical Journal,
Vol. 77,
Issue. ,
p.
13.
Kuz'min, L. V.
1987.
Algebraic number fields.
Journal of Soviet Mathematics,
Vol. 38,
Issue. 3,
p.
1930.


 -adic number field
-adic number field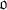 be the ring of all integers of
be the ring of all integers of 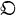 of all integers of
of all integers of 