No CrossRef data available.
Published online by Cambridge University Press: 22 January 2016
Let Ω be an open set in the upper half plane {y > 0}, whose boundary is denoted by ∂Ω. Let ∂Ω contain an open segment Γ lying on the x-axis.
We consider the following system of first order degenerating on y = 0:
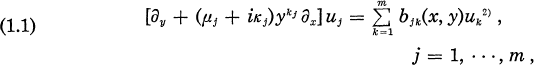
where kj, μj are real constants and bjk are in L∞(Ω), further kj are non-negative integers.
This work has been supported by Grant-in-Aid for Co-operative Research A organized by the Ministry of Education, the Japanese Government.