Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T11:10:20.206Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE HEIGHT AND RELATIONAL COMPLEXITY OF A FINITE PERMUTATION GROUP

Part of: Permutation groups

Published online by Cambridge University Press:  13 July 2021

NICK GILL Open the ORCID record for NICK GILL [Opens in a new window] ,
BIANCA LODÀ Open the ORCID record for BIANCA LODÀ [Opens in a new window]  and
PABLO SPIGA Open the ORCID record for PABLO SPIGA [Opens in a new window]
NICK GILL
Affiliation:
Department of Mathematics, University of South Wales, Treforest CF37 1DL, United [email protected]
BIANCA LODÀ
Affiliation:
Department of Mathematics, University of South Wales, TreforestCF37 1DL, United [email protected]
PABLO SPIGA
Affiliation:
Dipartimento di Matematica e Applicazioni, University of Milano-Bicocca, Via Cozzi 55, 20125Milano, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a permutation group on a set $\Omega $ of size t. We say that $\Lambda \subseteq \Omega $ is an independent set if its pointwise stabilizer is not equal to the pointwise stabilizer of any proper subset of 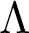$\Lambda $ . We define the height of G to be the maximum size of an independent set, and we denote this quantity 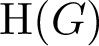$\textrm{H}(G)$ . In this paper, we study $\textrm{H}(G)$ for the case when G is primitive. 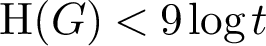Our main result asserts that either $\textrm{H}(G)< 9\log t$ or else G is in a particular well-studied family (the primitive large–base groups). An immediate corollary of this result is a characterization of primitive permutation groups with large relational complexity, the latter quantity being a statistic introduced by Cherlin in his study of the model theory of permutation groups. We also study 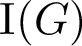$\textrm{I}(G)$ , the maximum length of an irredundant base of G, in which case we prove that if G is primitive, then either $\textrm{I}(G)<7\log t$ or else, again, G is in a particular family (which includes the primitive large–base groups as well as some others).

Keywords

permutation groupheight of a permutation grouprelational complexitybase size

MSC classification

Primary: 20B25: Finite automorphism groups of algebraic, geometric, or combinatorial structures
Secondary: 20B15: Primitive groups
Type
Article
Information
Nagoya Mathematical Journal , Volume 246 , June 2022 , pp. 372 - 411
Check for updates
Copyright
© (2021) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Nick Gill and Pablo Spiga would like to acknowledge the support of the Engineering and Physical Sciences Research Council grant EP/R028702/1 over the course of this research.

References

Babai, L., On the order of uniprimitive permutation groups, Ann. Math. (2) 113 (1981), 553–568.10.2307/2006997CrossRefGoogle Scholar
Blaha, K. D., Minimum bases for permutation groups: The greedy approximation, J. Algorithms 13 (1992), 297–306.10.1016/0196-6774(92)90020-DCrossRefGoogle Scholar
Bray, J. N., Holt, D. F., and Roney-Dougal, C. M., The Maximal Subgroups of the Low-Dimensional Finite Classical Groups, Cambridge University Press, Cambridge, MA, 2013.CrossRefGoogle Scholar
Burness, T. C., On base sizes for actions of finite classical groups, J. Lond. Math. Soc. (2) 75 (2007), 545–562.CrossRefGoogle Scholar
Burness, T. C. and Giudici, M., Classical Groups, Derangements and Primes, Aust. Math. Soc. Lect. Ser. 25, Cambridge University Press, Cambridge, MA, 2016.Google Scholar
Burness, T. C., Guralnick, R. M., and Saxl, J., On base sizes for symmetric groups, Bull. Lond. Math. Soc. 43 (2011), 386–391.CrossRefGoogle Scholar
Burness, T. C., Liebeck, M. W., and Shalev, A., Base sizes for simple groups and a conjecture of Cameron, Proc. Lond. Math. Soc. (3) 98 (2009), 116–162.10.1112/plms/pdn024CrossRefGoogle Scholar
Burness, T. C., O’Brien, E. A., and Wilson, R. A., Base sizes for sporadic simple groups, Israel J. Math. 177 (2010), 307–333.CrossRefGoogle Scholar
Cameron, P. J., “Some open problems on permutation groups” in Groups, Combinatorics and Geometry. Proceedings of the L.M.S. Durham Symposium, Held July 5–15, 1990 in Durham, UK, Cambridge University Press, Cambridge, MA, 1992, 340–350.Google Scholar
Cameron, P. J. and Kantor, W. M., “Random permutations: Some group-theoretic aspects” in Combinatorics, Geometry and Probability. A Tribute to Paul Erdős. Proceedings of the Conference Dedicated to Paul Erdős on the Occasion of His 80th Birthday, Cambridge, UK, 26 March 1993, Cambridge University Press, Cambridge, MA, 1997, 139–144.Google Scholar
Cameron, P. J., Solomon, R., and Turull, A., Chains of subgroups in symmetric groups, J. Algebra 127 (1989), 340–352.10.1016/0021-8693(89)90256-1CrossRefGoogle Scholar
Cherlin, G., On the relational complexity of a finite permutation group, J. Algebraic Combin. 43 (2016), 339–374.10.1007/s10801-015-0636-8CrossRefGoogle Scholar
Cherlin, G. L., Martin, G. A., and Saracino, D. H., Arities of permutation groups: Wreath products and $k$ -sets, J. Combin. Theory Ser. A 74 (1996), 249–286.CrossRefGoogle Scholar
Dixon, J. D. and Mortimer, B., Permutation Groups, Grad. Texts Math. 163, Springer, New York, 1996.Google Scholar
Guest, S., Morris, J., Praeger, C. E., and Spiga, P., On the maximum orders of elements of finite almost simple groups and primitive permutation groups, Trans. Amer. Math. Soc. 367 (2015), no. 11, 7665–7694.CrossRefGoogle Scholar
Kleidman, P. and Liebeck, M., The Subgroup Structure of the Finite Classical Groups, Lond. Math. Soc. Lect. Note Ser. 129, Cambridge University Press, Cambridge, MA, 1990.Google Scholar
Lang, S., Algebra, 3rd revised ed., Grad. Texts Math. 211, Springer, New York, 2002.Google Scholar
Liebeck, M. W., On minimal degrees and base sizes of primitive permutation groups, Arch. Math. 43 (1984), 11–15.CrossRefGoogle Scholar
Liebeck, M. W. and Shalev, A., Simple groups, permutation groups, and probability, J. Amer. Math. Soc. 12 (1999), 497–520.CrossRefGoogle Scholar
Moscatiello, M. and Roney-Dougal, C., Base sizes of primitive permutation groups, preprint available at https://arxiv.org/abs/2106.01219.Google Scholar
Praeger, C. E., The inclusion problem for finite primitive permutation groups, Proc. Lond. Math. Soc. (3) 60 (1990), 68–88.10.1112/plms/s3-60.1.68CrossRefGoogle Scholar
Quick, M., Probabilistic generation of wreath products of non-abelian finite simple groups, Comm. Algebra 32 (2004), 4753–4768.CrossRefGoogle Scholar