Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-11T13:10:16.808Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Gorensteinness of Rees algebras over local rings

Published online by Cambridge University Press:  22 January 2016

Shin Ikeda
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

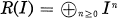Let (A, m, k) be a Noetherian local ring and I an ideal of A. We set and call this graded A-algebra the Rees algebra of I. The importance of the Rees algebra R(I) is in the fact that Proj R(I) is the blowing up of Spec A with center in V(I). The Cohen-Macaulayness of Rees algebras was studied by many mathematicians. In [GS] S. Goto any Y. Shimoda gave a criterion for R(m) to be Cohen-Macaulay under the assumption that A is Cohen-Macaulay. Their results have been generalized to R(I) in [HI].

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 102 , June 1986 , pp. 135 - 154
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1986

References

[A] Aoyama, Y., Some basic results on canonical modules, J. Math. Kyoto Univ., 23 (1983), 85–94.Google Scholar
[AG] Aoyama, Y. and Goto, S., On the type of graded Cohen-Macaulay rings, J. Math. Kyoto Univ., 15 (1975), 275–284.Google Scholar
[B] Bass, H., On the ubiquity of Gorenstein rings, Math. Z., 82 (1963), 8–28.CrossRefGoogle Scholar
[Gr1] Grothendieck, A., Sur quelque points d’algebre homologique, Tohoku Math. J., IX (1957), 119–221.Google Scholar
[Gr2] Grothendieck, A., Local cohomology, Lect. Notes in Math., 41, Berlin-Heidelberg-New York, 1967.Google Scholar
[GS] Goto, S. and Shimoda, Y., On the Rees algebras of Cohen-Macaulay local rings, Commutative algebra (analytic methods), Lecture Notes in Pure and Applied Mathematics, 68 (1982), 201–231.Google Scholar
[GW] Goto, S. and Watanabe, K., On graded rings I, J. Math. Soc. Japan, 30 (1978), 179–213.Google Scholar
[HI] Herrmann, M. and Ikeda, S., Remarks on lifting of Cohen-Macaulay property, Nagoya Math. J., 92 (1983), 121–132.CrossRefGoogle Scholar
[HK] Herzog, J. and Kunz, E., Der kanonische Modul eines Cohen-Macaulay Rings, Springer Lect. Notes in Math., 238 (1971).Google Scholar
[I1] Ikeda, S., The Cohen-Macaulayness of the Rees algebras of local rings, Nagoya Math. J., 89 (1983), 47–63.Google Scholar
[I2] Ikeda, S., Remarks on Rees algebras and graded rings with multiplicity 3, Preprint.Google Scholar
[M] Matlis, E., Infective modules over Noetherian rings, Pacific J. Math., 8 (1958), 511–528.CrossRefGoogle Scholar
[MR] Matijevic, J. and Roberts, P., A conjecture of Nagata on graded Cohen-Macaulay rings, J. Math. Kyoto Univ., 14 (1974) 125–128.Google Scholar
[NR] Northcott, D. G. and Rees, D., Reductions of ideals in local rings, Proc. Camb. Phil. Soc., 50 (1954), 145–158.Google Scholar
[CST] Cuong, N. T., Schenzel, P. and Trung, N. V., Verallgemeinerte Cohen-Macaulay-Moduln, Math. Nachr., 85 (1978), 57–73.Google Scholar