Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T06:05:39.742Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Gauss mean-value formula for class number

Published online by Cambridge University Press:  22 January 2016

Fernando Chamizo  and
Henryk Iwaniec
Fernando Chamizo
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad Autónoma de Madrid, 28049 Madrid, Spain, [email protected]
Henryk Iwaniec
Affiliation:
Department of Mathematics, Rutgers University, New Brunswick, NJ 08903, U.S.A., [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In his masterwork Disquisitiones Arithmeticae, Gauss stated an approximate formula for the average of the class number for negative discriminants. In this paper we improve the known estimates for the error term in Gauss approximate formula. Namely, our result can be written as 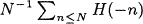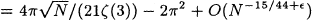for every ∊ > 0, where H(−n) is, in modern notation, h(−4n). We also consider the average of h(−n) itself obtaining the same type of result.

Proving this formula we transform firstly the problem in a lattice point problem (as probably Gauss did) and we use a functional equation due to Shintani and Dirichlet class number formula to express the error term as a sum of character and exponential sums that can be estimated with techniques introduced in a previous work on the sphere problem.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 151 , September 1998 , pp. 199 - 208
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1998

References

[Ch] Chen, Jing-Run, Improvement on the asymptotic formulas for the number of lattice points in a region of the three dimensions (II), Sci. Sinica, 12 N. 6 (1963), 751–764.Google Scholar
[Ch-Iw] Chamizo, F. and Iwaniec, H., On the sphere problem, Revista Mat. Iberoameri cana, 11, N. 2 (1995), 417–429.CrossRefGoogle Scholar
[Da] Davenport, H., Multiplicative Number Theory, Second edition, Graduate texts in Mathematics 74, Springer-Verlag, 1980.Google Scholar
[Di] Dirichlet, P. G. L., Vorlesungen über Zahlentheorie, (supplemented and revised by R. Dedekind), Braunschweig, 1863, (Reprinted by Chelsea Publishing Company, New York 1968).Google Scholar
[Ga] Gauss, C. F., Disquisitiones Arithmeticae, Leipzig, 1801, (English Translation by Clarke, A. A., Yale University Press, New Haven 1966).Google Scholar
[Gr-Ko] Graham, S. W. and Kolesnik, G., Van der Corput’s Method of Exponential Sums, London Math. Soc. Lecture Notes Series, 126, Cambridge University Press, 1991.CrossRefGoogle Scholar
[Gr-Ry] Gradshteyn, I.S. - Ryzhik, I.M.., Table of Integrals, Series and Products, Fifth edition (edited by Jeffrey, A.), Academic Press, 1994.Google Scholar
[Sh] Shintani, T., Zeta functions associated with the vector space of quadratic forms, J. Fac. Sci. Univ. Tokyo. Sect IA, 22 (1975), 22–65.Google Scholar
[Vi] Vinogradov, I.M., On the number of integer points in a sphere, Izv]. Akad. Nauk SSSR Ser. Mat., 27 (1963), 957–968, (Russian).Google Scholar