Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T23:17:13.088Z Has data issue: false hasContentIssue false
  • English
  • Français

On the fundamental units and the class numbers of real quadratic fields

Published online by Cambridge University Press:  22 January 2016

Takashi Azuhata
Takashi Azuhata*
Affiliation:
Department of Mathematics Science, University of Tokyo, 26 Wakamiya, Shinjuku-ku Tokyo, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

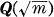Let Q be the rational number field and h(m) be the class number of the real quadratic field with a positive square-free integer m. It is known that if h(m) = 1 holds, then m is one of the following four types with prime numbers p ≡ 1, pt ≡ 3 (mod 4) (1 昤 i ≥ 4) : i) m = p, ii) m = p1, iii) m = 2 or m = 2p2, iv) m = p3p4 (see Behrbohm and Rédei [1]). The sufficient conditions for h(m) > 1 with these m were given by several authors: in all cases by Hasse [2], in case i) by Ankeny, Chowla and Hasse [3] and by Lang [4], in case ii) by Takeuchi [5] and by Yokoi [6].

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 95 , September 1984 , pp. 125 - 135
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1984

References

[ 1 ] Behrbohm, H. and Kédei, L., Der Euklidische Algorithmus in quadratischen Körpern, J. Reine Angew. Math., 174 (1936), 192–205.Google Scholar
[ 2 ] Hasse, H., Über mehrklassige, aber eingeschlechtige reellquadratischer Zahlkorper, Elem. Math., 29 (1965), 49–59.Google Scholar
[ 3 ] Ankeny, N.C., Chowla, S. and Hasse, H., On the class-number of the maximal real subfield of a cyclotomic field, J. Reine Angew. Math., 217 (1965), 217–220.Google Scholar
[ 4 ] Lang, S.D., Note on the class-number of the maximal real subfield of a cyclotomic field, J. Reine Angew. Math., 290 (1977), 70–72.Google Scholar
[ 5 ] Takeuchi, H., On the class-number of the maximal real subfield of a cyclotomic field, Canad. J. Math., 33 (1981), 55–58.CrossRefGoogle Scholar
[ 6 ] Yokoi, H., On the Diophantine equation x2 — py2 = ± 4q and the class number of real subfields of a cyclotomic field, Nagoya Math. J., 91 (1983), 151–161.CrossRefGoogle Scholar
[ 7 ] Dirichlet, P.G.L., Vorlesungen über Zahlentheorie, F. Vieweg & Shon, Braunschweig, 1894.Google Scholar
[ 8 ] Takagi, T., Shoto Seisuron Kogi (in Japanese), Kyoritsu, Tokyo, 1931.Google Scholar
[ 9 ] Degert, G., Über die Bestimmung der Grundeinheit gewisser reell-quadratischer Zahlkörper, Abh. Math. Sem. Univ. Hamburg, 22 (1958), 92–97.Google Scholar