Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T23:01:36.236Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Fundamental Existence Theorem of Kishi

Published online by Cambridge University Press:  22 January 2016

Mitsuru Nakai
Mitsuru Nakai*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Ω be a locally compact Hausdorff space and G(x, y) be a strictly positive lower semicontinuous function on the product space Ω×Ω of Ω. Such a function G(x, y) is called a kernel on Ω. The adjoint kernel Ğ(x, y) of G(x, y) is defined by Ğ(x, y) =G(y, x). Whenever we say a measure on Ω, we mean a positive regular Borel measure on Ω. The potential Gμ(x) and the adjoint potential Ğμ(x) of a measure μ relative to the kernel G(x, y) is defined by

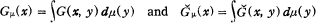
respectively. These are also strictly positive lower semicontinuous functions on Ω provided μ≠0.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 23 , December 1963 , pp. 189 - 198
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1963

References

[1] Brelot, M.: Éléments de la Théorie classique du Potentiel, 1959.Google Scholar
[2] Halmos, P. R.: Measure Theory, 1951.CrossRefGoogle Scholar
[3] Kakutani, S.: A Generalization of Brouwer’s fixed point theorem, Duke Math. J., Vol. 8 (1941), 457–459.CrossRefGoogle Scholar
[4] Kishi, M.: Note on balayage and maximum principles, Proc. Japan Acad., Vol.39 (1963), 415–418.Google Scholar
[5] Kishi, M.: Maximum principles in the potential theory, Nagoya Math. J., Vol. 23 (1963), 165–187.CrossRefGoogle Scholar
[6] Loomis, L. H.: An Introduction to abstract harmonic Analysis, 1953.Google Scholar
[7] Nikaidò, H.: Zusatz und Berichtigung fur meine Mitteilung “Zum Beweis der Verallgemeinerung des Fixpunktsatzes “ Kodai Math. Sem. Rep., Vol. 6 (1954), 11–12.Google Scholar