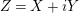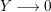1 Introduction and statement of result
Spaces of modular forms usually split up into the direct sum of the subspace generated by Eisenstein series and the subspace of cusp forms, and the Fourier coefficients of the latter, in general, satisfy much better bounds than those of the Eisenstein series. It is natural to ask conversely which bounds one may have to put on the general coefficients of a modular form to guarantee that it is already cuspidal.
This problem has recently attracted a reasonable amount of attention (see, for example, [Reference Böcherer and Das1–Reference Böcherer and Das3, Reference Kohnen8–Reference Linowitz10, Reference Mizuno12]). Specifically, in the papers [Reference Böcherer and Das1–Reference Böcherer and Das3], the case of a Siegel modular form
![]() $F$
of integral weight
$F$
of integral weight
![]() $k$
on a congruence subgroup
$k$
on a congruence subgroup
![]() $\unicode[STIX]{x1D6E4}$
of the Siegel modular group
$\unicode[STIX]{x1D6E4}$
of the Siegel modular group
![]() $\unicode[STIX]{x1D6E4}_{n}:=\text{Sp}_{n}(\mathbf{Z})$
of degree
$\unicode[STIX]{x1D6E4}_{n}:=\text{Sp}_{n}(\mathbf{Z})$
of degree
![]() $n$
was considered. Recall that if
$n$
was considered. Recall that if
![]() $F$
is cuspidal, then its Fourier coefficients at every cusp of
$F$
is cuspidal, then its Fourier coefficients at every cusp of
![]() $\unicode[STIX]{x1D6E4}$
are supported on positive definite matrixes
$\unicode[STIX]{x1D6E4}$
are supported on positive definite matrixes
![]() $T$
and satisfy the so-called Hecke bound
$T$
and satisfy the so-called Hecke bound
![]() $\ll _{F}(\det T)^{\frac{k}{2}}$
. Conversely, in [Reference Böcherer and Das2], it was shown that if
$\ll _{F}(\det T)^{\frac{k}{2}}$
. Conversely, in [Reference Böcherer and Das2], it was shown that if
![]() $k\geqslant 2n$
, and if the coefficients of
$k\geqslant 2n$
, and if the coefficients of
![]() $F$
at one cusp supported on positive definite
$F$
at one cusp supported on positive definite
![]() $T$
satisfy a bound
$T$
satisfy a bound
![]() $\ll _{F}(\det T)^{\unicode[STIX]{x1D6FC}}$
, where
$\ll _{F}(\det T)^{\unicode[STIX]{x1D6FC}}$
, where
![]() $\unicode[STIX]{x1D6FC}<k-n$
, then
$\unicode[STIX]{x1D6FC}<k-n$
, then
![]() $F$
already is a cusp form. In particular, if
$F$
already is a cusp form. In particular, if
![]() $k>2n$
and those coefficients satisfy the Hecke bound, then
$k>2n$
and those coefficients satisfy the Hecke bound, then
![]() $F$
is cuspidal. More generally, including the case of “small weights”, say
$F$
is cuspidal. More generally, including the case of “small weights”, say
![]() $k\geqslant \frac{n}{2}+1$
, corresponding statements were proved in [Reference Böcherer and Das3], for example with the condition
$k\geqslant \frac{n}{2}+1$
, corresponding statements were proved in [Reference Böcherer and Das3], for example with the condition
![]() $\unicode[STIX]{x1D6FC}<k-n$
relaxed to
$\unicode[STIX]{x1D6FC}<k-n$
relaxed to
![]() $\unicode[STIX]{x1D6FC}<k-\frac{n+3}{2}$
, under the additional hypothesis that
$\unicode[STIX]{x1D6FC}<k-\frac{n+3}{2}$
, under the additional hypothesis that
![]() $\unicode[STIX]{x1D6E4}$
is one of the generalized Hecke congruence subgroups
$\unicode[STIX]{x1D6E4}$
is one of the generalized Hecke congruence subgroups
![]() $\unicode[STIX]{x1D6E4}_{n,0}(N)$
of level
$\unicode[STIX]{x1D6E4}_{n,0}(N)$
of level
![]() $N$
. The tools used in [Reference Böcherer and Das1–Reference Böcherer and Das3] were quite deep, including in [Reference Böcherer and Das1, Reference Böcherer and Das2] the theory of
$N$
. The tools used in [Reference Böcherer and Das1–Reference Böcherer and Das3] were quite deep, including in [Reference Böcherer and Das1, Reference Böcherer and Das2] the theory of
![]() $L$
-functions, estimates for Hecke eigenvalues and certain local methods, while in [Reference Böcherer and Das3], Witt operators and the theory of Fourier–Jacobi expansions were employed.
$L$
-functions, estimates for Hecke eigenvalues and certain local methods, while in [Reference Böcherer and Das3], Witt operators and the theory of Fourier–Jacobi expansions were employed.
The purpose of this paper is to contribute a new idea of proof to the above subject, which is simple in the sense that it does not use any deeper structure theorems for the space of modular forms in question. In particular, it is not difficult to see that our arguments can be modified slightly to work also in the case of half-integral weight or for Jacobi forms, Hermitian modular forms or Hilbert–Siegel modular forms. At the same time, we can mildly improve upon or complement the results given in [Reference Böcherer and Das1–Reference Böcherer and Das3].
Our proof to a good part is modeled on some arguments given for
![]() $n=1$
(i.e. in the case of classical elliptic modular forms) by Miyake [Reference Miyake11, pp. 41–42]. They show that an elliptic modular form
$n=1$
(i.e. in the case of classical elliptic modular forms) by Miyake [Reference Miyake11, pp. 41–42]. They show that an elliptic modular form
![]() $f$
of weight
$f$
of weight
![]() $k$
on a subgroup of finite index of
$k$
on a subgroup of finite index of
![]() $\unicode[STIX]{x1D6E4}_{1}$
is cuspidal, if it satisfies an estimate
$\unicode[STIX]{x1D6E4}_{1}$
is cuspidal, if it satisfies an estimate
![]() $f(z)={\mathcal{O}}(y^{-c})$
for
$f(z)={\mathcal{O}}(y^{-c})$
for
![]() $y\rightarrow 0$
, uniformly in
$y\rightarrow 0$
, uniformly in
![]() $x$
(where
$x$
(where
![]() $z=x+iy$
, as usual), for some
$z=x+iy$
, as usual), for some
![]() $c<k$
. We show that these arguments can, in fact, be properly modified to work also in the case
$c<k$
. We show that these arguments can, in fact, be properly modified to work also in the case
![]() $n>1$
. Note that from the outset this is not clear at all; for example, for
$n>1$
. Note that from the outset this is not clear at all; for example, for
![]() $n>1$
, infinitely many degenerate Fourier coefficients occur and have to be handled appropriately. In the final part of the proof, we also use a “trick” by projecting down a modular form to its Fourier subseries (again modular) supported on indices
$n>1$
, infinitely many degenerate Fourier coefficients occur and have to be handled appropriately. In the final part of the proof, we also use a “trick” by projecting down a modular form to its Fourier subseries (again modular) supported on indices
![]() $T\equiv T_{0}\,(\text{mod}\,p)$
, where
$T\equiv T_{0}\,(\text{mod}\,p)$
, where
![]() $T_{0}$
is a fixed positive definite matrix and
$T_{0}$
is a fixed positive definite matrix and
![]() $p$
is an odd prime, chosen appropriately. We now state our result in detail.
$p$
is an odd prime, chosen appropriately. We now state our result in detail.
Theorem.
Let
![]() $\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{n}$
be a congruence subgroup, and let
$\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{n}$
be a congruence subgroup, and let
![]() $F$
be a Siegel modular form of integral weight
$F$
be a Siegel modular form of integral weight
![]() $k>n+1$
on
$k>n+1$
on
![]() $\unicode[STIX]{x1D6E4}$
. Assume that its Fourier coefficients
$\unicode[STIX]{x1D6E4}$
. Assume that its Fourier coefficients
![]() $a(T)$
(where
$a(T)$
(where
![]() $T$
is a positive definite half-integral matrix of size
$T$
is a positive definite half-integral matrix of size
![]() $n$
) at some cusp of
$n$
) at some cusp of
![]() $\unicode[STIX]{x1D6E4}$
satisfy the bound
$\unicode[STIX]{x1D6E4}$
satisfy the bound
where
![]() $\unicode[STIX]{x1D6FC}<k-\frac{n+1}{2}$
. Then,
$\unicode[STIX]{x1D6FC}<k-\frac{n+1}{2}$
. Then,
![]() $F$
is a cusp form.
$F$
is a cusp form.
Remarks.
(i) It follows from [Reference Kitaoka7, Theorem 1.6.23] that if
 $k\geqslant 2n+2$
, then the coefficients
$k\geqslant 2n+2$
, then the coefficients
 $a(T)$
(with
$a(T)$
(with
 $T$
positive definite) of any modular form
$T$
positive definite) of any modular form
 $F$
of weight
$F$
of weight
 $k$
on
$k$
on
 $\unicode[STIX]{x1D6E4}$
satisfy the estimate Thus, in general, the exponent
$\unicode[STIX]{x1D6E4}$
satisfy the estimate Thus, in general, the exponent $$\begin{eqnarray}a(T)\ll _{F}(\det T)^{k-\frac{n+1}{2}}.\end{eqnarray}$$
$$\begin{eqnarray}a(T)\ll _{F}(\det T)^{k-\frac{n+1}{2}}.\end{eqnarray}$$
 $\unicode[STIX]{x1D6FC}$
in (1) cannot be chosen larger.
$\unicode[STIX]{x1D6FC}$
in (1) cannot be chosen larger.(ii) If
 $n=1$
, then the assertion of the Theorem holds with
$n=1$
, then the assertion of the Theorem holds with
 $\unicode[STIX]{x1D6E4}$
replaced by an arbitrary Fuchsian subgroup of
$\unicode[STIX]{x1D6E4}$
replaced by an arbitrary Fuchsian subgroup of
 $\text{SL}_{2}(\mathbf{R})$
of the first kind (and so, in particular, for a subgroup of
$\text{SL}_{2}(\mathbf{R})$
of the first kind (and so, in particular, for a subgroup of
 $\unicode[STIX]{x1D6E4}_{1}$
of finite index). This follows easily by inspecting the arguments given in [Reference Miyake11, pp. 41–42].
$\unicode[STIX]{x1D6E4}_{1}$
of finite index). This follows easily by inspecting the arguments given in [Reference Miyake11, pp. 41–42].(iii) We recall that by the well-known “congruence subgroup theorem”, if
 $n\geqslant 2$
, any subgroup of
$n\geqslant 2$
, any subgroup of
 $\unicode[STIX]{x1D6E4}_{n}$
of finite index already is a congruence subgroup.
$\unicode[STIX]{x1D6E4}_{n}$
of finite index already is a congruence subgroup.
The actual proof of the theorem is given in Section 4. In Section 2, we prove some preparatory results needed later, while in Section 3 (proposition), we first give a preliminary version of the theorem. Finally, in Section 5, we comment on some possible generalizations of our results.
Notations. We denote by
![]() ${\mathcal{H}}_{n}$
the Siegel upper half-space of degree
${\mathcal{H}}_{n}$
the Siegel upper half-space of degree
![]() $n$
, consisting of symmetric complex
$n$
, consisting of symmetric complex
![]() $(n,n)$
-matrixes with positive imaginary part. If
$(n,n)$
-matrixes with positive imaginary part. If
![]() $Z\in {\mathcal{H}}_{n}$
, we write
$Z\in {\mathcal{H}}_{n}$
, we write
![]() $Z=X+iY$
, with
$Z=X+iY$
, with
![]() $X=\Re (Z)$
and
$X=\Re (Z)$
and
![]() $Y=\Im (Z)$
. The real symplectic group
$Y=\Im (Z)$
. The real symplectic group
![]() $\text{Sp}_{n}(\mathbf{R})$
operates on
$\text{Sp}_{n}(\mathbf{R})$
operates on
![]() ${\mathcal{H}}_{n}$
by
${\mathcal{H}}_{n}$
by
If
![]() $\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{n}$
is a congruence subgroup, we denote by
$\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{n}$
is a congruence subgroup, we denote by
![]() $M_{k}(\unicode[STIX]{x1D6E4})$
(resp.
$M_{k}(\unicode[STIX]{x1D6E4})$
(resp.
![]() $S_{k}(\unicode[STIX]{x1D6E4})$
) the space of Siegel modular forms (resp. cusp forms) of weight
$S_{k}(\unicode[STIX]{x1D6E4})$
) the space of Siegel modular forms (resp. cusp forms) of weight
![]() $k\in \mathbf{N}$
with respect to
$k\in \mathbf{N}$
with respect to
![]() $\unicode[STIX]{x1D6E4}$
. We assume that the reader is familiar with the elementary theory of Siegel modular forms, as for example is contained in [Reference Freitag5].
$\unicode[STIX]{x1D6E4}$
. We assume that the reader is familiar with the elementary theory of Siegel modular forms, as for example is contained in [Reference Freitag5].
We denote by
![]() $E_{n}$
(resp.
$E_{n}$
(resp.
![]() $0_{n}$
) the unit (resp. zero) matrix of size
$0_{n}$
) the unit (resp. zero) matrix of size
![]() $n$
. For matrixes
$n$
. For matrixes
![]() $A$
and
$A$
and
![]() $B$
of appropriate sizes we put as usual
$B$
of appropriate sizes we put as usual
![]() $A[B]:=B^{t}AB$
.
$A[B]:=B^{t}AB$
.
If
![]() $Y$
is a symmetric real matrix, we write
$Y$
is a symmetric real matrix, we write
![]() $Y>0$
(resp.
$Y>0$
(resp.
![]() $Y\geqslant 0$
) if
$Y\geqslant 0$
) if
![]() $Y$
is positive definite (resp. positive semi-definite). If
$Y$
is positive definite (resp. positive semi-definite). If
![]() $Y>0$
, we denote by
$Y>0$
, we denote by
![]() $Y^{1/2}$
the (uniquely determined) positive definite matrix whose square is
$Y^{1/2}$
the (uniquely determined) positive definite matrix whose square is
![]() $Y$
.
$Y$
.
If
![]() $g\in \text{Sp}_{n}(\mathbf{R})$
,
$g\in \text{Sp}_{n}(\mathbf{R})$
,
![]() $k\in \mathbf{N}$
, and
$k\in \mathbf{N}$
, and
![]() $F:{\mathcal{H}}_{n}\rightarrow \mathbf{C}$
is a function, we set
$F:{\mathcal{H}}_{n}\rightarrow \mathbf{C}$
is a function, we set
2 Some preparatory results
We may assume that
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{n}(N)$
is the principal congruence subgroup of level
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{n}(N)$
is the principal congruence subgroup of level
![]() $N$
. If
$N$
. If
![]() $F\in M_{k}(\unicode[STIX]{x1D6E4})$
, then
$F\in M_{k}(\unicode[STIX]{x1D6E4})$
, then
![]() $F$
at each cusp (say “represented” by
$F$
at each cusp (say “represented” by
![]() $g\in \unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}$
) has a Fourier expansion which has the form
$g\in \unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}$
) has a Fourier expansion which has the form
Here,
![]() $T$
runs over all positive semi-definite half-integral matrixes of size
$T$
runs over all positive semi-definite half-integral matrixes of size
![]() $n$
.
$n$
.
In particular, taking
![]() $g=E_{2n}$
, we have an expansion “at infinity”
$g=E_{2n}$
, we have an expansion “at infinity”
Since
![]() $\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{n}$
is a normal subgroup, without loss of generality, to prove the Theorem we may suppose that the estimate (1) holds “at infinity”; that is, for the numbers
$\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{n}$
is a normal subgroup, without loss of generality, to prove the Theorem we may suppose that the estimate (1) holds “at infinity”; that is, for the numbers
![]() $a(T)$
in (2). We then have to show that
$a(T)$
in (2). We then have to show that
![]() $a_{g}(T)=0$
for all
$a_{g}(T)=0$
for all
![]() $g\in \unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}$
and for all
$g\in \unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}$
and for all
![]() $T\geqslant 0$
that are not positive definite.
$T\geqslant 0$
that are not positive definite.
The following Lemma will be especially important to our arguments.
Lemma 1. One can choose representatives
![]() $g$
in
$g$
in
![]() $\unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}$
such that
$\unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}$
such that
![]() $g=\big(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!\big)$
, with
$g=\big(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!\big)$
, with
![]() $\det C\neq 0$
.
$\det C\neq 0$
.
Proof. We note that
![]() $\unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}\simeq \text{Sp}_{n}(\mathbf{Z}/N\mathbf{Z})$
. Choose a prime
$\unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}\simeq \text{Sp}_{n}(\mathbf{Z}/N\mathbf{Z})$
. Choose a prime
![]() $p$
not dividing
$p$
not dividing
![]() $N$
. According to the well-known “strong approximation theorem” (one can also argue here in an ad hoc and elementary way), there exists
$N$
. According to the well-known “strong approximation theorem” (one can also argue here in an ad hoc and elementary way), there exists
![]() $\tilde{g}\in \unicode[STIX]{x1D6E4}_{n}$
such that
$\tilde{g}\in \unicode[STIX]{x1D6E4}_{n}$
such that
Then,
![]() $\tilde{g}$
and
$\tilde{g}$
and
![]() $g$
represent the same class
$g$
represent the same class
![]() $(\text{mod}\,N)$
, and
$(\text{mod}\,N)$
, and
![]() $\det \tilde{C}\equiv 1\,(\text{mod}\,p)$
(where
$\det \tilde{C}\equiv 1\,(\text{mod}\,p)$
(where
![]() $\tilde{C}$
denotes the lower left block of
$\tilde{C}$
denotes the lower left block of
![]() $\tilde{g}$
). This proves the claim.◻
$\tilde{g}$
). This proves the claim.◻
Lemma 2. Suppose that
![]() $g=\big(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!\big)\in \text{Sp}_{n}(\mathbf{R})$
and
$g=\big(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!\big)\in \text{Sp}_{n}(\mathbf{R})$
and
![]() $\det C\neq 0$
. Then, for all
$\det C\neq 0$
. Then, for all
![]() $Z=X+iY\in {\mathcal{H}}_{n}$
, we have
$Z=X+iY\in {\mathcal{H}}_{n}$
, we have
Proof. This follows by a direct computation. Indeed, as is well-known,
Hence, observing that
![]() $C$
is invertible and the equation
$C$
is invertible and the equation
![]() $CD^{t}=DC^{t}$
, we find
$CD^{t}=DC^{t}$
, we find
 $$\begin{eqnarray}\displaystyle (\Im (g\circ Z))^{-1} & = & \displaystyle C(Z+C^{-1}D)Y^{-1}(\overline{Z}+C^{-1}D)C^{t}\nonumber\\ \displaystyle & = & \displaystyle C(iY+R)Y^{-1}(-iY+R)C^{t}\nonumber\\ \displaystyle & = & \displaystyle C(Y+Y^{-1}[R])C^{t},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\Im (g\circ Z))^{-1} & = & \displaystyle C(Z+C^{-1}D)Y^{-1}(\overline{Z}+C^{-1}D)C^{t}\nonumber\\ \displaystyle & = & \displaystyle C(iY+R)Y^{-1}(-iY+R)C^{t}\nonumber\\ \displaystyle & = & \displaystyle C(Y+Y^{-1}[R])C^{t},\nonumber\end{eqnarray}$$
where above we have put
Hence, we obtain
Taking inverses on both sides of (3), the assertion follows. (Observe that
![]() $Y_{1}\geqslant Y_{2}>0$
implies that
$Y_{1}\geqslant Y_{2}>0$
implies that
![]() $Y_{1}^{-1}\leqslant Y_{2}^{-1}$
, as follows by acting with
$Y_{1}^{-1}\leqslant Y_{2}^{-1}$
, as follows by acting with
![]() $[Y_{2}^{-1/2}]$
and taking inverses.)
$[Y_{2}^{-1/2}]$
and taking inverses.)
Recall that the series
(summation over all integral symmetric matrixes of size
![]() $n$
) is absolutely convergent for
$n$
) is absolutely convergent for
![]() $\unicode[STIX]{x1D70E}>n$
(cf., e.g., [Reference Siegel, Chandrasekharan and Maass13, Hilfssatz 38]).◻
$\unicode[STIX]{x1D70E}>n$
(cf., e.g., [Reference Siegel, Chandrasekharan and Maass13, Hilfssatz 38]).◻
Lemma 3. Let
![]() $\unicode[STIX]{x1D70E}>n$
and
$\unicode[STIX]{x1D70E}>n$
and
![]() $Y_{0}>0$
. Then, for
$Y_{0}>0$
. Then, for
![]() $Y\leqslant Y_{0}$
, one has
$Y\leqslant Y_{0}$
, one has
Proof. We write the sum on the left-hand side of (4) as
For
![]() $Y\leqslant Y_{0}$
, one has
$Y\leqslant Y_{0}$
, one has
as will follow from Lemma 4 below, and the expression on the right-hand side of (6) equals
Hence, we find that the sum in (5) is bounded from above by
and the latter sum is finite. This proves our assertion.◻
Lemma 4. Let
![]() $Y_{0}>0$
. Then, for all symmetric real matrixes
$Y_{0}>0$
. Then, for all symmetric real matrixes
![]() $R$
and
$R$
and
![]() $Y\leqslant Y_{0}$
, the estimate
$Y\leqslant Y_{0}$
, the estimate
holds.
Proof. We first get rid of
![]() $Y_{0}$
in (7). For this, we replace
$Y_{0}$
in (7). For this, we replace
![]() $R$
by
$R$
by
![]() $R[Y^{1/2}]$
, and then we have to prove that
$R[Y^{1/2}]$
, and then we have to prove that
for all
![]() $R=R^{t}$
and
$R=R^{t}$
and
![]() $Y\leqslant Y_{0}$
. The right-hand side is equal to
$Y\leqslant Y_{0}$
. The right-hand side is equal to
Writing
![]() $Y$
for
$Y$
for
![]() $Y_{0}[Y^{-1/2}]$
, we see that the original condition
$Y_{0}[Y^{-1/2}]$
, we see that the original condition
![]() $Y\leqslant Y_{0}$
becomes
$Y\leqslant Y_{0}$
becomes
![]() $Y\geqslant E_{n}$
and that under the latter condition we have to show that
$Y\geqslant E_{n}$
and that under the latter condition we have to show that
Note that here we can replace
![]() $Y$
by
$Y$
by
![]() $Y[U]$
, where
$Y[U]$
, where
![]() $U$
is orthogonal, and thus we can assume that
$U$
is orthogonal, and thus we can assume that
![]() $Y$
is diagonal. In a final step, we transform the right-hand side of (8) to
$Y$
is diagonal. In a final step, we transform the right-hand side of (8) to
replace
![]() $Y^{-1/2}$
by
$Y^{-1/2}$
by
![]() $Y$
and take squares.
$Y$
and take squares.
Then, we see that we have to prove that
for all
![]() $R=R^{t}$
and all diagonal matrixes
$R=R^{t}$
and all diagonal matrixes
![]() $Y\leqslant E_{n}$
. We denote the diagonal elements of
$Y\leqslant E_{n}$
. We denote the diagonal elements of
![]() $Y$
by
$Y$
by
![]() $y_{1},\ldots ,y_{n}$
.
$y_{1},\ldots ,y_{n}$
.
Since the determinant is linear in columns, for any
![]() $(n,n)$
-matrix
$(n,n)$
-matrix
![]() $C$
we have the equation
$C$
we have the equation
where
![]() $C_{i_{1}\ldots i_{\unicode[STIX]{x1D708}}}$
is the
$C_{i_{1}\ldots i_{\unicode[STIX]{x1D708}}}$
is the
![]() $(n,n)$
-matrix that arises from
$(n,n)$
-matrix that arises from
![]() $C$
by replacing the columns with indices
$C$
by replacing the columns with indices
![]() $i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}$
by the corresponding standard unit column vectors
$i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}$
by the corresponding standard unit column vectors
![]() $e_{i_{1}},\ldots ,e_{i_{\unicode[STIX]{x1D708}}}$
. Note that the cases
$e_{i_{1}},\ldots ,e_{i_{\unicode[STIX]{x1D708}}}$
. Note that the cases
![]() $\unicode[STIX]{x1D708}=0$
(resp.
$\unicode[STIX]{x1D708}=0$
(resp.
![]() $\unicode[STIX]{x1D708}=n$
) correspond to
$\unicode[STIX]{x1D708}=n$
) correspond to
![]() $\det C$
(resp. 1).
$\det C$
(resp. 1).
We apply this with
![]() $C:=R[Y]^{2}$
. We put
$C:=R[Y]^{2}$
. We put
![]() $A:=Y^{2}[R]$
. Then,
$A:=Y^{2}[R]$
. Then,
![]() $R[Y]^{2}=A[Y]$
, and we find
$R[Y]^{2}=A[Y]$
, and we find
From the Laplace expansion principle, we obtain
where the lower star in the notation means that double indices
![]() $ij$
with
$ij$
with
![]() $i=i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}$
and any
$i=i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}$
and any
![]() $j$
, or with
$j$
, or with
![]() $j=i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}$
and any
$j=i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}$
and any
![]() $i$
have to be omitted. It follows that
$i$
have to be omitted. It follows that
 $$\begin{eqnarray}\displaystyle \det (y_{i}y_{j}a_{ij})_{\ast } & = & \displaystyle \left(\mathop{\prod }_{i\neq i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}}y_{i}^{2}\right)\det (a_{ij})_{\ast }\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \det (a_{ij})_{\ast },\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \det (y_{i}y_{j}a_{ij})_{\ast } & = & \displaystyle \left(\mathop{\prod }_{i\neq i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}}y_{i}^{2}\right)\det (a_{ij})_{\ast }\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \det (a_{ij})_{\ast },\nonumber\end{eqnarray}$$
since by assumption
![]() $y_{i}\leqslant 1$
for all
$y_{i}\leqslant 1$
for all
![]() $i$
. (Note that
$i$
. (Note that
![]() $A$
, and hence also
$A$
, and hence also
![]() $(a_{ij})_{\ast }$
, is positive semi-definite.)
$(a_{ij})_{\ast }$
, is positive semi-definite.)
We now calculate backwards, that is with
![]() $Y$
replaced by
$Y$
replaced by
![]() $E_{n}$
in
$E_{n}$
in
![]() $A[Y]$
, and then we see that
$A[Y]$
, and then we see that
However, since
![]() $Y^{2}\leqslant E_{n}$
, we have
$Y^{2}\leqslant E_{n}$
, we have
![]() $Y^{2}[R]\leqslant E[R]=R^{2}$
, and therefore we conclude that
$Y^{2}[R]\leqslant E[R]=R^{2}$
, and therefore we conclude that
This proves what we wanted.◻
Remark.
Using the bound
![]() $\det (E_{n}+R)\geqslant 1+tr(R)$
, for any
$\det (E_{n}+R)\geqslant 1+tr(R)$
, for any
![]() $R\geqslant 0$
, one can also estimate the sum in (4) (up to a constant depending only on
$R\geqslant 0$
, one can also estimate the sum in (4) (up to a constant depending only on
![]() $Y_{0}$
) against the product of
$Y_{0}$
) against the product of
![]() $(\det Y)^{-\unicode[STIX]{x1D70E}}$
times the Epstein zeta function of the quadratic form
$(\det Y)^{-\unicode[STIX]{x1D70E}}$
times the Epstein zeta function of the quadratic form
![]() $\mathbf{Z}^{n(n+1)/2}\rightarrow \mathbf{Z},x\mapsto x^{t}x$
in
$\mathbf{Z}^{n(n+1)/2}\rightarrow \mathbf{Z},x\mapsto x^{t}x$
in
![]() $\frac{n(n+1)}{2}$
variables, evaluated at
$\frac{n(n+1)}{2}$
variables, evaluated at
![]() $\unicode[STIX]{x1D70E}/2$
. However, in this approach, because of convergence reasons, one has to suppose that
$\unicode[STIX]{x1D70E}/2$
. However, in this approach, because of convergence reasons, one has to suppose that
![]() $\unicode[STIX]{x1D70E}>\frac{n(n+1)}{2}$
(instead of
$\unicode[STIX]{x1D70E}>\frac{n(n+1)}{2}$
(instead of
![]() $\unicode[STIX]{x1D70E}>n$
in the above proof). Checking the further arguments, one finds that this leads to the stronger hypothesis
$\unicode[STIX]{x1D70E}>n$
in the above proof). Checking the further arguments, one finds that this leads to the stronger hypothesis
![]() $k>\frac{n(n+1)}{2}$
in the theorem.
$k>\frac{n(n+1)}{2}$
in the theorem.
Lemma 5. Let
![]() $R$
be a fixed symmetric real matrix of size
$R$
be a fixed symmetric real matrix of size
![]() $n$
. Then, the following assertions hold.
$n$
. Then, the following assertions hold.
(i) For any
 $Z=X+iY\in {\mathcal{H}}_{n}$
, one has
$Z=X+iY\in {\mathcal{H}}_{n}$
, one has  $$\begin{eqnarray}|\text{det}(Z+R)|\geqslant \det Y.\end{eqnarray}$$
$$\begin{eqnarray}|\text{det}(Z+R)|\geqslant \det Y.\end{eqnarray}$$
(ii) For any
 $Z=X+iY\in {\mathcal{H}}_{n}$
such that
$Z=X+iY\in {\mathcal{H}}_{n}$
such that
 $Y\geqslant Y_{0}>0$
and
$Y\geqslant Y_{0}>0$
and
 $X$
has bounded components, one has
$X$
has bounded components, one has  $$\begin{eqnarray}|\text{det}(Z+R)|\ll \det Y.\end{eqnarray}$$
$$\begin{eqnarray}|\text{det}(Z+R)|\ll \det Y.\end{eqnarray}$$
Proof.
(i) We may incorporate
 $R$
into
$R$
into
 $X$
. Then, the assertion is equivalent to saying that where
$X$
. Then, the assertion is equivalent to saying that where $$\begin{eqnarray}\det (AA^{t}+E_{n})\geqslant 1,\end{eqnarray}$$
$$\begin{eqnarray}\det (AA^{t}+E_{n})\geqslant 1,\end{eqnarray}$$
 $A:=X[Y^{-1/2}]$
. However, this is clear since
$A:=X[Y^{-1/2}]$
. However, this is clear since
 $AA^{t}\geqslant 0$
.
$AA^{t}\geqslant 0$
.(ii) We proceed in a similar way as in (i). Diagonalizing as usual with orthogonal matrixes, we observe that
 $Y\geqslant Y_{0}\geqslant cE_{n}$
(where
$Y\geqslant Y_{0}\geqslant cE_{n}$
(where
 $c>0$
) implies that the eigenvalues of
$c>0$
) implies that the eigenvalues of
 $Y^{-1}$
(and hence of
$Y^{-1}$
(and hence of
 $Y^{-1/2}$
) are bounded from above; hence,
$Y^{-1/2}$
) are bounded from above; hence,
 $Y^{-1/2}$
has bounded components. Hence, under our hypothesis on
$Y^{-1/2}$
has bounded components. Hence, under our hypothesis on
 $X$
, the same is true for
$X$
, the same is true for
 $A=X[Y^{-1/2}]$
, and it follows that
$A=X[Y^{-1/2}]$
, and it follows that
 $\det (AA^{t}+E_{n})\ll 1$
.◻
$\det (AA^{t}+E_{n})\ll 1$
.◻
3 A preliminary version of the theorem
We now prove the theorem first under the additional hypothesis that the Fourier expansion (2) of
![]() $F$
is supported on matrixes
$F$
is supported on matrixes
![]() $T>0$
only. (On the other hand, we need only the slightly weaker assumption
$T>0$
only. (On the other hand, we need only the slightly weaker assumption
![]() $k>n$
here.) More precisely, we have the following.
$k>n$
here.) More precisely, we have the following.
Proposition.
Assume that
![]() $k>n$
. Let
$k>n$
. Let
![]() $F\in M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
, suppose that the Fourier expansion (2) of
$F\in M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
, suppose that the Fourier expansion (2) of
![]() $F$
is supported on
$F$
is supported on
![]() $T>0$
and that
$T>0$
and that
where
![]() $\unicode[STIX]{x1D6FC}<k-\frac{n+1}{2}$
. Then,
$\unicode[STIX]{x1D6FC}<k-\frac{n+1}{2}$
. Then,
![]() $F$
is in
$F$
is in
![]() $S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
.
$S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
.
Proof. Our assumptions imply that
Let us recall the generalized Lipschitz formula (cf., e.g., [Reference Siegel, Chandrasekharan and Maass13, Hilfssatz 38]), which says that
Here,
![]() $Z\in {\mathcal{H}}_{n}$
,
$Z\in {\mathcal{H}}_{n}$
,
![]() $\unicode[STIX]{x1D70E}>n$
and
$\unicode[STIX]{x1D70E}>n$
and
We apply (10) with
![]() $Z=i\frac{1}{N}Y$
and
$Z=i\frac{1}{N}Y$
and
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FC}+\frac{n+1}{2}$
. Note that we may suppose that
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FC}+\frac{n+1}{2}$
. Note that we may suppose that
![]() $\unicode[STIX]{x1D6FC}>\frac{n-1}{2}$
in (1) (and so
$\unicode[STIX]{x1D6FC}>\frac{n-1}{2}$
in (1) (and so
![]() $\unicode[STIX]{x1D70E}>n$
). Indeed, if
$\unicode[STIX]{x1D70E}>n$
). Indeed, if
![]() $\unicode[STIX]{x1D6FC}\leqslant \frac{n-1}{2}$
, then
$\unicode[STIX]{x1D6FC}\leqslant \frac{n-1}{2}$
, then
(since
![]() $k>n$
by hypothesis), and we may replace
$k>n$
by hypothesis), and we may replace
![]() $\unicode[STIX]{x1D6FC}$
in (1) by some
$\unicode[STIX]{x1D6FC}$
in (1) by some
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
with
$\unicode[STIX]{x1D6FC}^{\prime }$
with
and continue the argument with
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
instead of
$\unicode[STIX]{x1D6FC}^{\prime }$
instead of
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
From (9) and Lemma 3 applied with
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FC}+\frac{n+1}{2}$
, we now find that
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FC}+\frac{n+1}{2}$
, we now find that
for any fixed
![]() $Y_{0}>0$
.
$Y_{0}>0$
.
The Fourier coefficients
![]() $a_{g}(T)$
have the usual expression,
$a_{g}(T)$
have the usual expression,
valid for any fixed
![]() $Y>0$
, where
$Y>0$
, where
![]() $g=\big(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!\big)$
.
$g=\big(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!\big)$
.
By Lemma 1, we may suppose that
![]() $C$
is invertible. Then, by Lemma 2, it follows that
$C$
is invertible. Then, by Lemma 2, it follows that
In the following few lines, we always tacitly suppose that
![]() $Y\geqslant Y_{0}>0$
.
$Y\geqslant Y_{0}>0$
.
Given this condition, we deduce that
Therefore, by (11), we find that
Inserting the latter inequality into (12), we obtain
From Lemma 5(i) applied with
![]() $R=C^{-1}D$
, we find that
$R=C^{-1}D$
, we find that
Moreover, under the additional condition that the components of
![]() $X$
are bounded, we have
$X$
are bounded, we have
(where in the last line we use Lemma 5(ii) with
![]() $R=C^{-1}D$
), and hence
$R=C^{-1}D$
), and hence
Inserting (14) and (15) into (13), we find that
The last inequality holds for any
![]() $Y\geqslant Y_{0}>0$
.
$Y\geqslant Y_{0}>0$
.
Now, let us suppose that
![]() $T$
is degenerate. We choose a unimodular matrix
$T$
is degenerate. We choose a unimodular matrix
![]() $U$
such that
$U$
such that
with
![]() $T_{1}$
of size
$T_{1}$
of size
![]() $0\leqslant r<n$
and
$0\leqslant r<n$
and
![]() $T_{1}$
invertible. Note that
$T_{1}$
invertible. Note that
and choose
![]() $Y>0$
in such a way that
$Y>0$
in such a way that
is a diagonal matrix with
![]() $D_{1}=E_{r}$
and
$D_{1}=E_{r}$
and
![]() $D_{4}=yE_{n-r}$
, with
$D_{4}=yE_{n-r}$
, with
![]() $y>0$
. Then, clearly,
$y>0$
. Then, clearly,
 $$\begin{eqnarray}\displaystyle Y & = & \displaystyle \left(\begin{array}{@{}cc@{}}D_{1} & 0\\ 0 & D_{4}\end{array}\right)[U]\nonumber\\ \displaystyle & {\geqslant} & \displaystyle Y_{0}:=E_{n}[U],\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y & = & \displaystyle \left(\begin{array}{@{}cc@{}}D_{1} & 0\\ 0 & D_{4}\end{array}\right)[U]\nonumber\\ \displaystyle & {\geqslant} & \displaystyle Y_{0}:=E_{n}[U],\nonumber\end{eqnarray}$$
for
![]() $y\geqslant 1$
. Moreover,
$y\geqslant 1$
. Moreover,
is constant. Since
letting
![]() $y\rightarrow \infty$
we obtain from (16) that
$y\rightarrow \infty$
we obtain from (16) that
![]() $a_{g}(T)=0$
, provided that
$a_{g}(T)=0$
, provided that
![]() $\unicode[STIX]{x1D6FC}+\frac{n+1}{2}-k<0$
. Hence,
$\unicode[STIX]{x1D6FC}+\frac{n+1}{2}-k<0$
. Hence,
![]() $F$
is cuspidal, as claimed. This proves the proposition.◻
$F$
is cuspidal, as claimed. This proves the proposition.◻
4 Proof of theorem
We now remove the additional hypothesis made in the proposition in Section 3.
If
![]() $F$
and
$F$
and
![]() $G$
are in
$G$
are in
![]() $M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
, and at least one of them is a cusp form, we denote by
$M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
, and at least one of them is a cusp form, we denote by
 $$\begin{eqnarray}\displaystyle & \displaystyle \langle F,G\rangle =\frac{1}{[\unicode[STIX]{x1D6E4}_{n}:\unicode[STIX]{x1D6E4}_{n}(N)]}\int _{\unicode[STIX]{x1D6E4}_{n}(N)\backslash {\mathcal{H}}_{n}}F(Z)\overline{G(Z)}(\det Y)^{k}\,d\unicode[STIX]{x1D714} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(Z=X+iY,dw=\frac{dXdY}{(\det Y)^{n+1}}\right) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \langle F,G\rangle =\frac{1}{[\unicode[STIX]{x1D6E4}_{n}:\unicode[STIX]{x1D6E4}_{n}(N)]}\int _{\unicode[STIX]{x1D6E4}_{n}(N)\backslash {\mathcal{H}}_{n}}F(Z)\overline{G(Z)}(\det Y)^{k}\,d\unicode[STIX]{x1D714} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(Z=X+iY,dw=\frac{dXdY}{(\det Y)^{n+1}}\right) & \displaystyle \nonumber\end{eqnarray}$$
the normalized Petersson bracket of
![]() $F$
and
$F$
and
![]() $G$
. Note that the value
$G$
. Note that the value
![]() $\langle F,G\rangle$
is independent of the level of which
$\langle F,G\rangle$
is independent of the level of which
![]() $F$
and
$F$
and
![]() $G$
are considered to be modular, and that
$G$
are considered to be modular, and that
![]() $\langle ,\rangle$
defines a scalar product on
$\langle ,\rangle$
defines a scalar product on
![]() $S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
.
$S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
.
Let
be in
![]() $M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
. Let
$M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
. Let
![]() $T_{0}>0$
, and let
$T_{0}>0$
, and let
![]() $p$
be an odd prime. (The choice of
$p$
be an odd prime. (The choice of
![]() $p$
being odd is only for notational convenience.) Then, we define
$p$
being odd is only for notational convenience.) Then, we define
Lemma 6.
(i) One has
 $F_{T_{0},p}\in M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
.
$F_{T_{0},p}\in M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
.(ii) If
 $\langle F,G\rangle =0$
for all
$\langle F,G\rangle =0$
for all
 $G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
, then
$G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
, then
 $\langle F_{T_{0},p},G\rangle =0$
for all
$\langle F_{T_{0},p},G\rangle =0$
for all
 $G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
.
$G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
.
Proof. This is proved in a standard way. For any symmetric real matrix
![]() $S$
, let us put
$S$
, let us put
(i) The usual orthogonality relations for roots of unity show that
where the sum extends over all integral symmetric matrixes
![]() $S\,(\text{mod}\,p)$
. Since
$S\,(\text{mod}\,p)$
. Since
![]() $F$
is modular with respect to
$F$
is modular with respect to
![]() $\unicode[STIX]{x1D6E4}_{n}(N)$
, each summand on the right-hand side is modular with respect to
$\unicode[STIX]{x1D6E4}_{n}(N)$
, each summand on the right-hand side is modular with respect to
![]() $\unicode[STIX]{x1D6E4}_{n}(Np^{2})$
, as is easily checked. Hence, we deduce that
$\unicode[STIX]{x1D6E4}_{n}(Np^{2})$
, as is easily checked. Hence, we deduce that
![]() $F_{T_{0},p}$
is in
$F_{T_{0},p}$
is in
![]() $M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
.
$M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
.
(ii) Let
![]() $G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
. Then, the usual formalism of the Petersson bracket shows that
$G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
. Then, the usual formalism of the Petersson bracket shows that
 $$\begin{eqnarray}\displaystyle p^{\frac{n(n+1)}{2}}\langle F_{T_{0},p},G\rangle & = & \displaystyle \mathop{\sum }_{S=S^{t}\,(\text{mod}\,p)}e^{-2\unicode[STIX]{x1D70B}itr(T_{0}S/p)}\langle F|_{k}\unicode[STIX]{x1D6FE}_{n,NS/p},G\rangle \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{S=S^{t}\,(\text{mod}\,p)}e^{-2\unicode[STIX]{x1D70B}itr(T_{0}S/p)}\langle F,G|_{k}\unicode[STIX]{x1D6FE}_{n,-NS/p}\rangle .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p^{\frac{n(n+1)}{2}}\langle F_{T_{0},p},G\rangle & = & \displaystyle \mathop{\sum }_{S=S^{t}\,(\text{mod}\,p)}e^{-2\unicode[STIX]{x1D70B}itr(T_{0}S/p)}\langle F|_{k}\unicode[STIX]{x1D6FE}_{n,NS/p},G\rangle \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{S=S^{t}\,(\text{mod}\,p)}e^{-2\unicode[STIX]{x1D70B}itr(T_{0}S/p)}\langle F,G|_{k}\unicode[STIX]{x1D6FE}_{n,-NS/p}\rangle .\nonumber\end{eqnarray}$$
Note that
![]() $G|_{k}\unicode[STIX]{x1D6FE}_{n,-NS/p}$
is modular with respect to
$G|_{k}\unicode[STIX]{x1D6FE}_{n,-NS/p}$
is modular with respect to
![]() $\unicode[STIX]{x1D6E4}_{n}(Np^{4})$
(cf. (i)). Thus, we obtain
$\unicode[STIX]{x1D6E4}_{n}(Np^{4})$
(cf. (i)). Thus, we obtain
where
 $$\begin{eqnarray}\displaystyle & \displaystyle tr_{Np^{4}}^{N}:M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{4}))\rightarrow M_{k}(\unicode[STIX]{x1D6E4}_{n}(N)), & \displaystyle \nonumber\\ \displaystyle & \displaystyle H\mapsto \frac{1}{[\unicode[STIX]{x1D6E4}_{n}(N):\unicode[STIX]{x1D6E4}_{n}(Np^{4})]}\mathop{\sum }_{L\in \unicode[STIX]{x1D6E4}_{n}(Np^{4})\backslash \unicode[STIX]{x1D6E4}_{n}(N)}H|_{k}L & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle tr_{Np^{4}}^{N}:M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{4}))\rightarrow M_{k}(\unicode[STIX]{x1D6E4}_{n}(N)), & \displaystyle \nonumber\\ \displaystyle & \displaystyle H\mapsto \frac{1}{[\unicode[STIX]{x1D6E4}_{n}(N):\unicode[STIX]{x1D6E4}_{n}(Np^{4})]}\mathop{\sum }_{L\in \unicode[STIX]{x1D6E4}_{n}(Np^{4})\backslash \unicode[STIX]{x1D6E4}_{n}(N)}H|_{k}L & \displaystyle \nonumber\end{eqnarray}$$
is the usual trace map (adjoint to the inclusion map on subspaces of cusp forms). Since with
![]() $H$
also
$H$
also
![]() $tr_{Np^{4}}^{N}(H)$
is cuspidal, our hypothesis implies that the right-hand side of (18) is zero, as was to be shown.
$tr_{Np^{4}}^{N}(H)$
is cuspidal, our hypothesis implies that the right-hand side of (18) is zero, as was to be shown.
We now prove the Theorem. By elementary linear algebra, there is a decomposition
where
Let
![]() $F\in M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
, and suppose that (1) holds. We may assume that
$F\in M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
, and suppose that (1) holds. We may assume that
![]() $\frac{k}{2}\leqslant \unicode[STIX]{x1D6FC}$
. Otherwise,
$\frac{k}{2}\leqslant \unicode[STIX]{x1D6FC}$
. Otherwise,
![]() $\unicode[STIX]{x1D6FC}<\frac{k}{2}$
, and then the bound (1) would imply that also
$\unicode[STIX]{x1D6FC}<\frac{k}{2}$
, and then the bound (1) would imply that also
![]() $a(T)\ll (\det T)^{k/2}$
, and we can finish the argument with
$a(T)\ll (\det T)^{k/2}$
, and we can finish the argument with
![]() $\unicode[STIX]{x1D6FC}$
replaced by
$\unicode[STIX]{x1D6FC}$
replaced by
![]() $\unicode[STIX]{x1D6FC}^{\prime }=\frac{k}{2}$
. Note that
$\unicode[STIX]{x1D6FC}^{\prime }=\frac{k}{2}$
. Note that
![]() $\frac{k}{2}<k-\frac{n+1}{2}$
since
$\frac{k}{2}<k-\frac{n+1}{2}$
since
![]() $k>n+1$
by hypothesis.
$k>n+1$
by hypothesis.
We write
![]() $F=F_{1}+F_{2}$
, with
$F=F_{1}+F_{2}$
, with
![]() $F_{1}\in C_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
and
$F_{1}\in C_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
and
![]() $F_{2}\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
according to (19). By the assumption
$F_{2}\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$
according to (19). By the assumption
![]() $\frac{k}{2}\leqslant \unicode[STIX]{x1D6FC}$
, and since the Fourier coefficients of cusp forms satisfy the bound
$\frac{k}{2}\leqslant \unicode[STIX]{x1D6FC}$
, and since the Fourier coefficients of cusp forms satisfy the bound
![]() $\ll (\det T)^{k/2}$
, the
$\ll (\det T)^{k/2}$
, the
![]() $T$
th Fourier coefficients
$T$
th Fourier coefficients
![]() $b(T)\,(T>0)$
of
$b(T)\,(T>0)$
of
![]() $F_{1}=F-F_{2}$
satisfy (1). Suppose that there exists
$F_{1}=F-F_{2}$
satisfy (1). Suppose that there exists
![]() $T_{0}>0$
with
$T_{0}>0$
with
![]() $b(T_{0})\neq 0$
. Let
$b(T_{0})\neq 0$
. Let
![]() $p$
be an odd prime not dividing
$p$
be an odd prime not dividing
![]() $\det (2T_{0})$
. Then, the function
$\det (2T_{0})$
. Then, the function
![]() $(F_{1})_{T_{0},p}$
defined by (17) is in
$(F_{1})_{T_{0},p}$
defined by (17) is in
![]() $M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
, by Lemma 6(i), and has Fourier coefficients supported on positive definite matrixes which again satisfy (1) by definition (17). Therefore, by the proposition,
$M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
, by Lemma 6(i), and has Fourier coefficients supported on positive definite matrixes which again satisfy (1) by definition (17). Therefore, by the proposition,
![]() $(F_{1})_{T_{0},p}$
is a cusp form. At the same time, by Lemma 6(ii),
$(F_{1})_{T_{0},p}$
is a cusp form. At the same time, by Lemma 6(ii),
for all
![]() $G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
. Hence, we conclude that
$G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$
. Hence, we conclude that
![]() $(F_{1})_{T_{0},p}=0$
. In particular,
$(F_{1})_{T_{0},p}=0$
. In particular,
![]() $b(T_{0})=0$
, a contradiction. Therefore, the Fourier expansion of
$b(T_{0})=0$
, a contradiction. Therefore, the Fourier expansion of
![]() $F_{1}$
is supported on degenerate matrixes; that is,
$F_{1}$
is supported on degenerate matrixes; that is,
![]() $F_{1}$
is a singular modular form and we necessarily must have
$F_{1}$
is a singular modular form and we necessarily must have
![]() $k<\frac{n}{2}$
unless
$k<\frac{n}{2}$
unless
![]() $F_{1}=0$
(see, for example, [Reference Freitag5]). However,
$F_{1}=0$
(see, for example, [Reference Freitag5]). However,
![]() $k>n+1$
by assumption, and so we finally conclude that
$k>n+1$
by assumption, and so we finally conclude that
![]() $F=F_{2}$
is cuspidal.
$F=F_{2}$
is cuspidal.
This proves the theorem.◻
5 Generalizations
Our method seems to be rather robust and very flexible. We essentially only need growth properties of the modular form
![]() $F(Z)$
in question when
$F(Z)$
in question when
![]() $\det Y\rightarrow 0$
(in an appropriate way). These, in turn, rely on the generalized Lipschitz formula. In particular, essentially no arithmetic is involved, and therefore issues like class numbers should play no role in generalizations. We now briefly comment on cases of interest.
$\det Y\rightarrow 0$
(in an appropriate way). These, in turn, rely on the generalized Lipschitz formula. In particular, essentially no arithmetic is involved, and therefore issues like class numbers should play no role in generalizations. We now briefly comment on cases of interest.
(i) Nonintegral weights. There should be no problem at all for nonintegral weights (including not only the half-integral weight case, but also more general rational weights for the group
![]() $GL(2)$
).
$GL(2)$
).
(ii) Orthogonal modular forms. Modular forms on
![]() $\text{SO}(2,n)$
can be treated in a similar was as here. Note that
$\text{SO}(2,n)$
can be treated in a similar was as here. Note that
![]() $\text{SO}(2,3)$
is isogenous to
$\text{SO}(2,3)$
is isogenous to
![]() $\text{Sp}(2)$
.
$\text{Sp}(2)$
.
(iii) Jacobi forms. There is no real new issue here, also for Jacobi forms of higher degree. (For the basic theory we refer to [Reference Eichler and Zagier4, Reference Ziegler14].) One uses theta expansions and observes that the coefficients in these theta expansions give vectors of modular forms associated with a (projective) representation of finite co-kernel. In other words, we consider ordinary (Siegel) modular forms of lower degree, lower (possibly half-integral) weight and higher level. We note that the case of classical Jacobi forms was first treated in [Reference Kohnen and Martin9], using quite a different method.
(iv) Hermitian modular forms. The only new point here is the class number of the imaginary quadratic field in question. We just point out that in Section 4 it is not really necessary to use an integral matrix to transform a (symmetric or Hermitian) matrix into the form
![]() $\big(\!\begin{smallmatrix}\ast & 0\\ 0 & 0\end{smallmatrix}\!\big)$
; one can do this as well with a matrix whose coefficients are in the field in question.
$\big(\!\begin{smallmatrix}\ast & 0\\ 0 & 0\end{smallmatrix}\!\big)$
; one can do this as well with a matrix whose coefficients are in the field in question.
(v) Hilbert (–Siegel) modular forms. Our setting allows a straightforward application to the Hilbert modular case. It suffices to look at imaginary parts of type
![]() $(y,\ldots ,y)\in \mathbf{R}_{+}^{n}$
in the variables of such a form and let
$(y,\ldots ,y)\in \mathbf{R}_{+}^{n}$
in the variables of such a form and let
![]() $y\rightarrow 0$
. Here,
$y\rightarrow 0$
. Here,
![]() $n$
is the degree of the totally real number field in question. An extension to Hilbert–Siegel modular forms is also immediate. We mention that the case of Hilbert modular forms (using different techniques) in an adelic setting was previously treated in [Reference Linowitz10].
$n$
is the degree of the totally real number field in question. An extension to Hilbert–Siegel modular forms is also immediate. We mention that the case of Hilbert modular forms (using different techniques) in an adelic setting was previously treated in [Reference Linowitz10].
(vi) Vector-valued modular forms. For a finite dimensional complex vector space
![]() $V$
and a polynomial representation
$V$
and a polynomial representation
![]() $\unicode[STIX]{x1D70C}:GL(n,\mathbf{C})\rightarrow GL(V)$
, one can consider
$\unicode[STIX]{x1D70C}:GL(n,\mathbf{C})\rightarrow GL(V)$
, one can consider
![]() $V$
-valued Siegel modular forms with respect to the automorphy factor
$V$
-valued Siegel modular forms with respect to the automorphy factor
![]() $\unicode[STIX]{x1D70C}$
. The Hecke bound for cusp forms
$\unicode[STIX]{x1D70C}$
. The Hecke bound for cusp forms
![]() $F$
can then be stated as
$F$
can then be stated as
for some constant
![]() $C>0$
(see [Reference Godement6]), where
$C>0$
(see [Reference Godement6]), where
![]() $\Vert \,\Vert$
is the norm on
$\Vert \,\Vert$
is the norm on
![]() $V$
which comes from a scalar product on
$V$
which comes from a scalar product on
![]() $V$
, such that the group
$V$
, such that the group
![]() $U(n,\mathbf{C})$
acts unitarily and
$U(n,\mathbf{C})$
acts unitarily and
![]() $(a_{F}(T))\in V$
is the vector of Fourier coefficients of
$(a_{F}(T))\in V$
is the vector of Fourier coefficients of
![]() $F$
. We may decompose
$F$
. We may decompose
![]() $\unicode[STIX]{x1D70C}$
as
$\unicode[STIX]{x1D70C}$
as
![]() $\unicode[STIX]{x1D70C}_{0}\otimes \det ^{k}$
with the largest positive integer
$\unicode[STIX]{x1D70C}_{0}\otimes \det ^{k}$
with the largest positive integer
![]() $k$
such that
$k$
such that
![]() $\unicode[STIX]{x1D70C}_{0}$
is still a polynomial representation. Then, we may call
$\unicode[STIX]{x1D70C}_{0}$
is still a polynomial representation. Then, we may call
![]() $k$
the weight of
$k$
the weight of
![]() $\unicode[STIX]{x1D70C}$
. The estimate above then reads
$\unicode[STIX]{x1D70C}$
. The estimate above then reads
It is not immediately clear how to deduce from this an estimate for the behavior of
![]() $F$
when
$F$
when
![]() $\det Y$
goes to zero, information that seems to be necessary to get started at all with our approach. Moreover, an appropriate substitute for the Lipschitz formula seems to be missing.
$\det Y$
goes to zero, information that seems to be necessary to get started at all with our approach. Moreover, an appropriate substitute for the Lipschitz formula seems to be missing.
Note, however, that the approach via Hecke operators chosen in [Reference Böcherer and Das2] leads to some positive results in this setting.