Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T23:48:38.921Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence of various bounded harmonic functions with given periods, II

Published online by Cambridge University Press:  22 January 2016

Masaru Hara
Masaru Hara*
Affiliation:
Applied physics
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a harmonic function u on a Riemann surface R, we define a period function

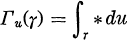
for every one-dimensional cycle γ of the Riemann surface R. Γx(R) denote the totality of period functions Γu such that harmonic functions u satisfy a boundedness property X. As for X, we let B stand for boundedness, and D for the finiteness of the Dirichlet integral.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 56 , January 1975 , pp. 1 - 5
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1975

References

[1] Hara, M.: On the existence of various bounded harmonic functions with given periods, Nagoya Math. J. (to appear).Google Scholar
[2] Sario, L. and Nakai, M.: Classification Theory of Riemann Surfaces. Springer (1970).CrossRefGoogle Scholar