Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T22:12:37.184Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence and boundedness of square function operators on Campanato spaces

Published online by Cambridge University Press:  22 January 2016

Yongzhong Sun
Yongzhong Sun*
Affiliation:
Depatment of Mathematics, Nanjing University, Nanjing, Jiangsu, P. R. China, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let g(f) be a Littlewood-Paley square function of f, which belongs to Campanato spaces . We prove that if g(f)(x0) exists (i.e. g(f)(x0) < ∞) for a single point x0 ∈ Rn, then g(f)(x) exists almost everywhere in Rn and 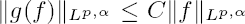. Thus we give an improvement of some earlier results such as in [8], where it is always needed to assume g(f)(x) exists in a set of positive measure in order to get the a.e. existence and boundedness of g(f)(x).

Keywords

42B2542B30
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 173 , 2004 , pp. 139 - 151
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2004

References

[1] Campanato, S., Proprietà di hölderianità di alcune di funzioni, Ann. Scuola Norm. Sup. Pisa, 17 (1963), 175–188.Google Scholar
[2] Fabes, F. B., Janson, R. L. & Neri, U., Spaces of harmonic functions representable by Poisson integrals of functions in BMO and Lp,λ , Indiana Univ. Math. J., 25 (1976), 159–170.Google Scholar
[3] Kurtz, D. S., Littlewood-Paley operators on BMO, Proc. Amer. Math. Soc., 99 (1987), 657–666.CrossRefGoogle Scholar
[4] Torchinsky, A., Realvariable methods in harmonic analysis, Academic Press, San Diego, Calif., 1986.Google Scholar
[5] Wang, Shilin, Boundedness of the Littlewood-Paley g-functions on Lipα(ℝn) (0 < α < 1), Ill. J. Math., 33 (1989), 531–541.Google Scholar
[6] Silei, Wang, Some properties of g-functions, Science in China, Series A, 10 (1984), 890–899.Google Scholar
[7] Silei, Wang & Jiecheng, Chen, Some notes on square function operator, Chinese Annals of Mathematics, Series A, 11 (1990), 630–638.Google Scholar
[8] Yabuta, K., Boundedness of Littlewood-Paley operators, Math. Japonica, 43 (1996), 143–150.Google Scholar