Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T23:22:13.271Z Has data issue: false hasContentIssue false
  • English
  • Français

On the equivalence problem and integration of differential systems

Published online by Cambridge University Press:  22 January 2016

Tatsuo Higa
Tatsuo Higa*
Affiliation:
Department of Mathematics, Faculty of Science Rikkyo University Ikebukuro, Tokyo 171, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of the presnet paper is to study the relationship between the theory of Lie pseudogroups and the problem of integration of differential systems (cf. [6] pp. 30-47).

Let 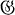be a Lie pseudogroup on a manifold M and S a differentia] system on M. Let 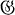(S) denote the largest subpseudogroup of 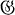leaving S invariant. Then the problems to be considered may be stated as follows.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 106 , June 1987 , pp. 49 - 77
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1987

References

[ 1 ] Cartan, E., Sur l’integration des systèmes différentiels complètement intégrables, C. R. Acad. Se, t. 134 (1902), 1415–1418 et 1564–1566.Google Scholar
[ 2 ] Cartan, E., Les sous-groupes des groupes continus de transformations, Ann. Ec. Norm., 25 (1908), 57–194.Google Scholar
[ 3 ] Cartan, E., Les systèmes de Pfaff à cinq variables et les équations aux dérivées partielles du second ordre, Ann. Ec. Norm., 27 (1910), 109–192.Google Scholar
[ 4 ] Cartan, E., Sur les systèmes en involution d’équations aux dérivées partielles du second ordre à une fonction inconnue de trois variables indépendantes, Oeuvres complètes, Partie II, vol. 2, 1035–1125.Google Scholar
[ 5 ] Cartan, E., Les systèmes différentiels extérieurs et leurs applications géométriques, Hermann, Paris, 1945.Google Scholar
[ 6 ] Cartan, E., Notice sur les travaux scientifiques, Oeuvres complètes, Partie I, vol. 1, 1–112.Google Scholar
[ 7 ] Higa, T., On the isomorphic reduction of an invariant associated with a Lie pseudo-group, Comment. Math. Univ. St. Paul., 34 (1985), 163–175.Google Scholar
[ 8 ] Johnson, H. H., Classical differential invariants and applications to partial differential equations, Math. Ann., 148 (1962), 308–329.CrossRefGoogle Scholar
[ 9 ] Kumpera, A., Invariants différentiels d’un pseudogroupe de Lie, I, J. Differential Geom., 10 (1975), 289–345.Google Scholar
[10] Morimoto, T., Sur le problème d’équivalence des structures géométriques, Japan J. Math., New Series, 9 (1983), 293–372.CrossRefGoogle Scholar
[11] Singer, I. M. and Sternberg, S., The infinite groups of Lie and Cartan, Part I, J. Analyse Math., 15 (1965), 1–114.CrossRefGoogle Scholar
[12] Sternberg, S., Lectures on Differential Geometry, Prentice-Hall, New Jersey, 1964.Google Scholar