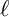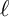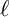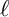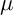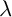1 Introduction
1.1 Classical Iwasawa theory
Let
![]() $\ell $
be a prime number, let K be a number field, and let
$\ell $
be a prime number, let K be a number field, and let
![]() $\mathbb {Z}_\ell $
denote the ring of
$\mathbb {Z}_\ell $
denote the ring of
![]() $\ell $
-adic integers. A
$\ell $
-adic integers. A
![]() $\mathbb {Z}_\ell $
-tower over K consists of a sequence of abelian extensions
$\mathbb {Z}_\ell $
-tower over K consists of a sequence of abelian extensions
such that for all values of n, the Galois group
![]() $\operatorname {Gal}(K_n/K)$
is isomorphic to
$\operatorname {Gal}(K_n/K)$
is isomorphic to
![]() $\mathbb {Z}/\ell ^n\mathbb {Z}$
. The union
$\mathbb {Z}/\ell ^n\mathbb {Z}$
. The union
![]() $K_\infty :=\bigcup _{n\geq 1} K_n$
is an infinite Galois extension of K with Galois group
$K_\infty :=\bigcup _{n\geq 1} K_n$
is an infinite Galois extension of K with Galois group
![]() $\operatorname {Gal}(K_\infty /K)$
isomorphic to
$\operatorname {Gal}(K_\infty /K)$
isomorphic to
![]() $\mathbb {Z}_\ell $
. We refer to
$\mathbb {Z}_\ell $
. We refer to
![]() $K_\infty $
as a
$K_\infty $
as a
![]() $\mathbb {Z}_\ell $
-extension of K. For
$\mathbb {Z}_\ell $
-extension of K. For
![]() $n\geq 0$
, we denote by
$n\geq 0$
, we denote by
![]() $\operatorname {Cl}_{\ell }(K_n)$
, the Sylow
$\operatorname {Cl}_{\ell }(K_n)$
, the Sylow
![]() $\ell $
-subgroup of the ideal class group of
$\ell $
-subgroup of the ideal class group of
![]() $K_n$
, and by
$K_n$
, and by
![]() $h_\ell (K_n)$
the cardinality of
$h_\ell (K_n)$
the cardinality of
![]() $\operatorname {Cl}_{\ell }(K_n)$
. In his seminal work [Reference Iwasawa10], Iwasawa studied growth patterns for
$\operatorname {Cl}_{\ell }(K_n)$
. In his seminal work [Reference Iwasawa10], Iwasawa studied growth patterns for
![]() $h_\ell (K_n)$
, as
$h_\ell (K_n)$
, as
![]() $n\rightarrow \infty $
. More specifically, it is shown in [Reference Iwasawa10] that there are invariants
$n\rightarrow \infty $
. More specifically, it is shown in [Reference Iwasawa10] that there are invariants
![]() $\mu $
,
$\mu $
,
![]() $\lambda ,$
and
$\lambda ,$
and
![]() $\nu $
, which only depend on the prime
$\nu $
, which only depend on the prime
![]() $\ell $
and the extension
$\ell $
and the extension
![]() $K_\infty $
(and independent of n), such that for
$K_\infty $
(and independent of n), such that for
![]() $n\gg 0$
,
$n\gg 0$
,
The quantities
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
are nonnegative integers, whereas the quantity
$\lambda $
are nonnegative integers, whereas the quantity
![]() $\nu $
is an integer, possibly negative.
$\nu $
is an integer, possibly negative.
Of special interest is the case when
![]() $K_\infty /K$
is the cyclotomic
$K_\infty /K$
is the cyclotomic
![]() $\mathbb {Z}_\ell $
-extension of K, in which case, we simply denote the Iwasawa invariants by
$\mathbb {Z}_\ell $
-extension of K, in which case, we simply denote the Iwasawa invariants by
![]() $\mu _\ell (K)$
,
$\mu _\ell (K)$
,
![]() $\lambda _\ell (K),$
and
$\lambda _\ell (K),$
and
![]() $\nu _\ell (K)$
. By the celebrated result of Ferrero and Washington [Reference Ferrero and Washington5],
$\nu _\ell (K)$
. By the celebrated result of Ferrero and Washington [Reference Ferrero and Washington5],
![]() $\mu _\ell (K)$
is equal to
$\mu _\ell (K)$
is equal to
![]() $0$
for all abelian extensions
$0$
for all abelian extensions
![]() $K/\mathbb {Q}$
. Moreover, it is conjectured in [Reference Iwasawa and Kusunoki11] that
$K/\mathbb {Q}$
. Moreover, it is conjectured in [Reference Iwasawa and Kusunoki11] that
![]() $\mu _\ell (K)$
is
$\mu _\ell (K)$
is
![]() $0$
for all number fields K. The
$0$
for all number fields K. The
![]() $\lambda $
-invariant is more subtle, and it is natural to study statistical questions about its average behavior.
$\lambda $
-invariant is more subtle, and it is natural to study statistical questions about its average behavior.
Let
![]() $n>0$
be an integer, and let
$n>0$
be an integer, and let
![]() $\mathcal {F}$
be a family of number fields of fixed degree n. We do not provide an explicit definition of what constitutes a family, however, it is natural to study number fields satisfying prescribed splitting conditions at a fixed set of primes. For instance, it is natural to consider the case when
$\mathcal {F}$
be a family of number fields of fixed degree n. We do not provide an explicit definition of what constitutes a family, however, it is natural to study number fields satisfying prescribed splitting conditions at a fixed set of primes. For instance, it is natural to consider the case when
![]() $\mathcal {F}$
is the family of imaginary quadratic fields in which p is inert (or split). For a number field K, we let
$\mathcal {F}$
is the family of imaginary quadratic fields in which p is inert (or split). For a number field K, we let
![]() $|\Delta _K|$
be the absolute discriminant. Given a real number
$|\Delta _K|$
be the absolute discriminant. Given a real number
![]() $x>0$
, let
$x>0$
, let
![]() $\mathcal {F}_{\leq x}$
be the subset of
$\mathcal {F}_{\leq x}$
be the subset of
![]() $\mathcal {F}$
consisting of number fields K such that
$\mathcal {F}$
consisting of number fields K such that
![]() $|\Delta _K|\leq x$
. Given
$|\Delta _K|\leq x$
. Given
![]() $\mu _0\geq 0$
and
$\mu _0\geq 0$
and
![]() $\lambda _0\geq 0$
and a real number
$\lambda _0\geq 0$
and a real number
![]() $x>0$
, we let
$x>0$
, we let
![]() $\mathcal {F}_{\leq x}(\mu _0, \lambda _0, \ell )$
consist of
$\mathcal {F}_{\leq x}(\mu _0, \lambda _0, \ell )$
consist of
![]() $K\in \mathcal {F}_{\leq x}$
such that
$K\in \mathcal {F}_{\leq x}$
such that
![]() $\mu _\ell (K)=\mu _0$
and
$\mu _\ell (K)=\mu _0$
and
![]() $\lambda _\ell (K)=\lambda _0$
. Note that both
$\lambda _\ell (K)=\lambda _0$
. Note that both
![]() $\mathcal {F}_{\leq x}$
and
$\mathcal {F}_{\leq x}$
and
![]() $\mathcal {F}_{\leq x}(\mu _0, \lambda _0, \ell )$
are finite sets. The following question motivates the line of inquiry in this manuscript.
$\mathcal {F}_{\leq x}(\mu _0, \lambda _0, \ell )$
are finite sets. The following question motivates the line of inquiry in this manuscript.
Question 1.1. Fix a prime number
![]() $\ell $
. Can one compute the proportion of number fields K in
$\ell $
. Can one compute the proportion of number fields K in
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mu =\mu _0$
and
$\mu =\mu _0$
and
![]() $\lambda =\lambda _0$
. In greater detail, one is interested in computing the density defined as follows:
$\lambda =\lambda _0$
. In greater detail, one is interested in computing the density defined as follows:
 $$\begin{align*}\mathfrak{d}(\mu_0, \lambda_0, \ell)=\lim_{x\rightarrow \infty} \frac{\#\mathcal{F}_{\leq x} (\mu_0, \lambda_0, \ell)}{\# \mathcal{F}_{\leq x}},\end{align*}$$
$$\begin{align*}\mathfrak{d}(\mu_0, \lambda_0, \ell)=\lim_{x\rightarrow \infty} \frac{\#\mathcal{F}_{\leq x} (\mu_0, \lambda_0, \ell)}{\# \mathcal{F}_{\leq x}},\end{align*}$$
in cases when the above limit exists.
This can be regarded as an analog of similar questions on classical Iwasawa invariants of number fields. The heuristics for the distribution of these arithmetic Iwasawa invariants have been studied by Ellenberg, Jain, and Venkatesh [Reference Ellenberg, Jain and Venkatesh4]. One may attempt to compute the limit above for various choices of
![]() $(\mu _0, \lambda _0)$
. Of course, the
$(\mu _0, \lambda _0)$
. Of course, the
![]() $\mu =0$
conjecture would imply that
$\mu =0$
conjecture would imply that
![]() $\mathfrak {d}(\mu _0, \lambda _0, \ell )=0$
if
$\mathfrak {d}(\mu _0, \lambda _0, \ell )=0$
if
![]() $\mu _0>0$
. It turns out that the above question, though of considerable interest, leads to difficulties that are yet to be resolved systematically.
$\mu _0>0$
. It turns out that the above question, though of considerable interest, leads to difficulties that are yet to be resolved systematically.
1.2 Iwasawa theory of multigraphs
In the present article, we consider graph-theoretic analogs of Iwasawa invariants, for which questions similar to Question 1.1 become tractable for certain families of multigraphs. What might be called the Iwasawa theory of multigraphs is a recent area of research. The reader may refer to [Reference McGown and Vallières19], [Reference McGown and Vallières20], and [Reference Vallières26] where the approach via Artin–Ihara L-functions is introduced and to [Reference Gonet8] where the module theoretical approach was initiated. Other articles on the subject where the reader can find more information are [Reference DuBose and Vallières3], [Reference Kataoka12], [Reference Kleine and Müller14], [Reference Lei and Vallières16], and [Reference Ray and Vallières22]. However, at present, there is no standard text on the subject.
A finite multigraph X consists of a finite set of vertices joined by directed edges and an inversion map satisfying prescribed properties. For the precise definition of a multigraph, the reader is referred to Definition 2.1. In this article, we allow there to be more than one edge joining any two vertices. We also allow for loops based at a single vertex. It is assumed that there are only finitely many edges, and the multigraph is connected. Given a prime
![]() $\ell $
, a connected
$\ell $
, a connected
![]() $\mathbb {Z}_\ell $
-tower over X consists of a sequence of covers of connected multigraphs
$\mathbb {Z}_\ell $
-tower over X consists of a sequence of covers of connected multigraphs
such that for every integer
![]() $n\geq 0$
, the Galois group
$n\geq 0$
, the Galois group
![]() $\operatorname {Gal}(X_n/X)$
is isomorphic to
$\operatorname {Gal}(X_n/X)$
is isomorphic to
![]() $\mathbb {Z}/\ell ^n \mathbb {Z}$
. Note that such a tower is not necessarily unique. The multigraphs
$\mathbb {Z}/\ell ^n \mathbb {Z}$
. Note that such a tower is not necessarily unique. The multigraphs
![]() $X_n$
can be constructed from a
$X_n$
can be constructed from a
![]() $\mathbb {Z}_\ell $
-valued voltage assignment on the edges of X. For further details, please refer to §2.2 where this construction is summarized. We establish a sufficient condition for
$\mathbb {Z}_\ell $
-valued voltage assignment on the edges of X. For further details, please refer to §2.2 where this construction is summarized. We establish a sufficient condition for
![]() $X_n$
to be connected for all
$X_n$
to be connected for all
![]() $n\ge 0$
(see Theorem 2.15). This particular criterion is potentially of independent interest. The inverse limit
$n\ge 0$
(see Theorem 2.15). This particular criterion is potentially of independent interest. The inverse limit
![]() $\varprojlim _n \operatorname {Gal}(X_n/X)$
is isomorphic to
$\varprojlim _n \operatorname {Gal}(X_n/X)$
is isomorphic to
![]() $\mathbb {Z}_\ell $
, and thus, a
$\mathbb {Z}_\ell $
, and thus, a
![]() $\mathbb {Z}_\ell $
-tower of a multigraph is analogous to a
$\mathbb {Z}_\ell $
-tower of a multigraph is analogous to a
![]() $\mathbb {Z}_\ell $
-extension of a number field. The Picard group
$\mathbb {Z}_\ell $
-extension of a number field. The Picard group
![]() $\operatorname {Pic}^0(X_n)$
has cardinality equal to the number of spanning trees in
$\operatorname {Pic}^0(X_n)$
has cardinality equal to the number of spanning trees in
![]() $X_n$
, for more details, compare [Reference Sunada24, Th. 10.8]. The cardinality of the Sylow
$X_n$
, for more details, compare [Reference Sunada24, Th. 10.8]. The cardinality of the Sylow
![]() $\ell $
-subgroup of
$\ell $
-subgroup of
![]() $\operatorname {Pic}^0(X_n)$
is denoted by
$\operatorname {Pic}^0(X_n)$
is denoted by
![]() $\kappa _\ell (X_n)$
. It is shown by McGown and the fourth named author (cf. [Reference McGown and Vallières19], [Reference McGown and Vallières20], [Reference Vallières26]) that there are invariants
$\kappa _\ell (X_n)$
. It is shown by McGown and the fourth named author (cf. [Reference McGown and Vallières19], [Reference McGown and Vallières20], [Reference Vallières26]) that there are invariants
![]() $\mu , \lambda \in \mathbb {Z}_{\geq 0}$
and
$\mu , \lambda \in \mathbb {Z}_{\geq 0}$
and
![]() $\nu \in \mathbb {Z}$
such that
$\nu \in \mathbb {Z}$
such that
for
![]() $n\gg 0$
. This establishes an analog of Iwasawa’s formula (1.1) in the setting of multigraphs. The formula (1.2) was also independently obtained by Gonet (see [Reference Gonet7], [Reference Gonet8]). We prove that when
$n\gg 0$
. This establishes an analog of Iwasawa’s formula (1.1) in the setting of multigraphs. The formula (1.2) was also independently obtained by Gonet (see [Reference Gonet7], [Reference Gonet8]). We prove that when
![]() $\ell $
is odd, the invariant
$\ell $
is odd, the invariant
![]() $\lambda $
is in fact always an odd integer (see Theorem 2.18), which again may be of independent interest.
$\lambda $
is in fact always an odd integer (see Theorem 2.18), which again may be of independent interest.
1.3 Main results
The main goal of the present article is to study the distribution of Iwasawa
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
-invariants for multigraphs that feature in (1.2). We study two related questions in this context. First, we fix a multigraph X and allow the
$\lambda $
-invariants for multigraphs that feature in (1.2). We study two related questions in this context. First, we fix a multigraph X and allow the
![]() $\mathbb {Z}_\ell $
-tower over X to vary in a natural way and study the variation of Iwasawa invariants. These investigations are carried out for multigraphs with one or two vertices as well as certain families of
$\mathbb {Z}_\ell $
-tower over X to vary in a natural way and study the variation of Iwasawa invariants. These investigations are carried out for multigraphs with one or two vertices as well as certain families of
![]() $\mathbb {Z}_\ell $
-towers of complete graphs. We expect that the methods developed in the present article can be generalized to many more families of multigraphs. However, the calculations may become cumbersome for general multigraphs. The second theme is more closely related to arithmetic statistics. Here, we consider all multigraphs with a given number of vertices, and their connected
$\mathbb {Z}_\ell $
-towers of complete graphs. We expect that the methods developed in the present article can be generalized to many more families of multigraphs. However, the calculations may become cumbersome for general multigraphs. The second theme is more closely related to arithmetic statistics. Here, we consider all multigraphs with a given number of vertices, and their connected
![]() $\mathbb {Z}_\ell $
-towers and study the variation of
$\mathbb {Z}_\ell $
-towers and study the variation of
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
-invariants for this entire family. This question can be formulated for multigraphs with a fixed number of vertices N for any number N. However, we find that the computations are significantly involved even in the case when
$\lambda $
-invariants for this entire family. This question can be formulated for multigraphs with a fixed number of vertices N for any number N. However, we find that the computations are significantly involved even in the case when
![]() $N=1$
. We refer to question (2) for the precise formulation of the problem in this setting. Below is a more detailed description of the results we prove.
$N=1$
. We refer to question (2) for the precise formulation of the problem in this setting. Below is a more detailed description of the results we prove.
-
1. In §4, we give a detailed analysis of the setting where X is a bouquet (a multigraph with a single vertex). In particular:
-
(a) We first establish several sufficient and/or necessary conditions for
 $\mu =0$
. This allows us to prove that
$\mu =0$
. This allows us to prove that
 $\mu $
is always zero and give an upper bound on
$\mu $
is always zero and give an upper bound on
 $\lambda $
under the hypothesis that
$\lambda $
under the hypothesis that
 $\ell $
is larger than the number of loops in a bouquet (see Corollary 4.3 and Theorem 4.13 for the precise statements). Without this hypothesis, we show that both
$\ell $
is larger than the number of loops in a bouquet (see Corollary 4.3 and Theorem 4.13 for the precise statements). Without this hypothesis, we show that both
 $\mu $
and
$\mu $
and
 $\lambda $
can be arbitrarily large (see Lemma 2.17), which mirrors similar results in the setting of Iwasawa theory of number fields and elliptic curves (see [Reference Iwasawa and Kusunoki11], [Reference Kim13], [Reference Kundu and Ray15], [Reference Matsuno18]).
$\lambda $
can be arbitrarily large (see Lemma 2.17), which mirrors similar results in the setting of Iwasawa theory of number fields and elliptic curves (see [Reference Iwasawa and Kusunoki11], [Reference Kim13], [Reference Kundu and Ray15], [Reference Matsuno18]). -
(b) Let t be the number of loops in a bouquet. We study the distribution of
 $\mu $
and
$\mu $
and
 $\lambda $
as the
$\lambda $
as the
 $\mathbb {Z}_\ell $
-tower varies. As we shall see in §2.2, where we review the Iwasawa theory of multigraphs, the connected
$\mathbb {Z}_\ell $
-tower varies. As we shall see in §2.2, where we review the Iwasawa theory of multigraphs, the connected
 $\mathbb {Z}_\ell $
-towers of a bouquet with t loops are in one–one correspondence with
$\mathbb {Z}_\ell $
-towers of a bouquet with t loops are in one–one correspondence with
 $\mathbb {Z}_\ell ^t\setminus (\ell \mathbb {Z}_\ell )^t$
. In particular, the Haar measure on
$\mathbb {Z}_\ell ^t\setminus (\ell \mathbb {Z}_\ell )^t$
. In particular, the Haar measure on
 $\mathbb {Z}_\ell $
gives a measure on the set of all connected
$\mathbb {Z}_\ell $
gives a measure on the set of all connected
 $\mathbb {Z}_\ell $
-towers of a given bouquet. Under this measure, we are able to obtain an upper bound on the probability for
$\mathbb {Z}_\ell $
-towers of a given bouquet. Under this measure, we are able to obtain an upper bound on the probability for
 $\mu>0$
, and for
$\mu>0$
, and for
 $\mu =0$
with a fixed choice of
$\mu =0$
with a fixed choice of
 $\lambda $
which is sufficiently small (see Theorems 4.6 and 4.16). For
$\lambda $
which is sufficiently small (see Theorems 4.6 and 4.16). For
 $\mu =0$
and
$\mu =0$
and
 $\lambda =1$
, we are able to prove a precise formula (see Theorem 4.18). We also investigate the cases where
$\lambda =1$
, we are able to prove a precise formula (see Theorem 4.18). We also investigate the cases where
 $t=2,3$
separately in §4.3.
$t=2,3$
separately in §4.3. -
(c) Specializing to the case where the
 $\mathbb {Z}_\ell $
-towers correspond to the vectors
$\mathbb {Z}_\ell $
-towers correspond to the vectors
 $\alpha =(\alpha _1,\ldots ,\alpha _t)\in \mathbb {Z}^t\setminus (\ell \mathbb {Z})^t$
, we show in Theorem 4.21 that as both t and
$\alpha =(\alpha _1,\ldots ,\alpha _t)\in \mathbb {Z}^t\setminus (\ell \mathbb {Z})^t$
, we show in Theorem 4.21 that as both t and
 $\alpha $
vary, the probability of
$\alpha $
vary, the probability of
 $\mu =0$
and
$\mu =0$
and
 $\lambda =1$
is equal to
$\lambda =1$
is equal to
 $1-\ell ^{-1}$
, mirroring a similar result obtained by the first and third named authors in the context of 2-bridge links (see [Reference Dion and Ray2, Th. 5.4]).
$1-\ell ^{-1}$
, mirroring a similar result obtained by the first and third named authors in the context of 2-bridge links (see [Reference Dion and Ray2, Th. 5.4]).
-
-
2. In §5, we study multigraphs with two vertices. In particular, we determine a precise formula for the probability of a
 $\mathbb {Z}_\ell $
-tower of a given multigraph with two vertices to have
$\mathbb {Z}_\ell $
-tower of a given multigraph with two vertices to have
 $\mu =0$
and
$\mu =0$
and
 $\lambda =1$
via the theory of quadratic forms over finite fields (see, in particular, Theorem 5.3).
$\lambda =1$
via the theory of quadratic forms over finite fields (see, in particular, Theorem 5.3). -
3. Finally, we study
 $\mathbb {Z}_\ell $
-towers of complete graphs. In particular, Theorem 6.4 gives a precise description of the distribution of
$\mathbb {Z}_\ell $
-towers of complete graphs. In particular, Theorem 6.4 gives a precise description of the distribution of
 $\mu $
and
$\mu $
and
 $\lambda $
for certain families including the so-called cyclic voltage covers of the complete graph
$\lambda $
for certain families including the so-called cyclic voltage covers of the complete graph
 $K_u$
with u vertices (which were initially studied by Gonet [Reference Gonet6]) as u varies.
$K_u$
with u vertices (which were initially studied by Gonet [Reference Gonet6]) as u varies.
1.4 Outlook
The present article initiates the study of distributions of Iwasawa invariants of multigraphs and answers several statistical questions in some special cases. Our main results rely crucially on studying the power series in
![]() $\mathbb {Z}_\ell [\![ T]\!]$
that governs the growth formula (1.2). For example, in order to study when
$\mathbb {Z}_\ell [\![ T]\!]$
that governs the growth formula (1.2). For example, in order to study when
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =1$
occurs, we are faced with the task of analyzing whether the leading term of the aforementioned power series is divisible by
$\lambda =1$
occurs, we are faced with the task of analyzing whether the leading term of the aforementioned power series is divisible by
![]() $\ell $
. In the cases being treated, we are able to reformulate this question in terms of explicit quadratic forms over
$\ell $
. In the cases being treated, we are able to reformulate this question in terms of explicit quadratic forms over
![]() $\mathbb {F}_\ell $
and employ results on finite fields (e.g., the Chevalley–Warning theorem). On developing further results on systems of equations over finite fields in several variables, one may study more than one coefficient of a power series in
$\mathbb {F}_\ell $
and employ results on finite fields (e.g., the Chevalley–Warning theorem). On developing further results on systems of equations over finite fields in several variables, one may study more than one coefficient of a power series in
![]() $\mathbb {Z}_\ell [\![ T]\!]$
simultaneously. This should then allow us to extend our results on
$\mathbb {Z}_\ell [\![ T]\!]$
simultaneously. This should then allow us to extend our results on
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =1$
to more general combinations of Iwasawa invariants. As mentioned above, carrying out similar calculations beyond the cases we have studied so far can potentially be cumbersome. It would be desirable to develop a systematic approach to study the questions inaugurated in the present article for more general families of graphs and multigraphs. For example, it would be very interesting to extend our methods to study distributions of Iwasawa invariants that arise from Erdös–Rényi random graphs. We plan to study some of these questions in the future.
$\lambda =1$
to more general combinations of Iwasawa invariants. As mentioned above, carrying out similar calculations beyond the cases we have studied so far can potentially be cumbersome. It would be desirable to develop a systematic approach to study the questions inaugurated in the present article for more general families of graphs and multigraphs. For example, it would be very interesting to extend our methods to study distributions of Iwasawa invariants that arise from Erdös–Rényi random graphs. We plan to study some of these questions in the future.
2 Preliminaries
This section is dedicated to the discussion of preliminary notions in this article.
2.1 Basic properties of multigraphs
Fix a prime number
![]() $\ell $
. We introduce basic notions in the theory of multigraphs and Iwasawa theory of
$\ell $
. We introduce basic notions in the theory of multigraphs and Iwasawa theory of
![]() $\mathbb {Z}_\ell $
-towers. For further details, the reader may refer to [Reference Lei and Vallières16, Sec. 2] and [Reference McGown and Vallières20, Sec. 4]. A finite undirected graph X consists of a finite set
$\mathbb {Z}_\ell $
-towers. For further details, the reader may refer to [Reference Lei and Vallières16, Sec. 2] and [Reference McGown and Vallières20, Sec. 4]. A finite undirected graph X consists of a finite set
![]() $V_X$
of vertices
$V_X$
of vertices
![]() $\{v_1, \dots , v_n\}$
, and a finite number of edges
$\{v_1, \dots , v_n\}$
, and a finite number of edges
![]() $E_X$
joining the vertices. For such a graph, there is at most one edge which joins
$E_X$
joining the vertices. For such a graph, there is at most one edge which joins
![]() $v_i$
and
$v_i$
and
![]() $v_j$
. Thus, in this context, we may view
$v_j$
. Thus, in this context, we may view
![]() $E_X$
as a subset of
$E_X$
as a subset of
![]() $V_X\times V_X$
. More specifically, if there is an edge joining
$V_X\times V_X$
. More specifically, if there is an edge joining
![]() $v_i$
to
$v_i$
to
![]() $v_j$
, then
$v_j$
, then
![]() $(v_i, v_j)$
belongs to
$(v_i, v_j)$
belongs to
![]() $E_X$
. Since the graph X in question is undirected, we have that
$E_X$
. Since the graph X in question is undirected, we have that
![]() $(v_i, v_j)\in E_X$
if and only if
$(v_i, v_j)\in E_X$
if and only if
![]() $(v_j, v_i)\in E_X$
. An edge from
$(v_j, v_i)\in E_X$
. An edge from
![]() $v_i$
to
$v_i$
to
![]() $v_i$
is referred to as a loop. The graph X is fully described by the pair
$v_i$
is referred to as a loop. The graph X is fully described by the pair
![]() $(V_X, E_X)$
. On the other hand, a directed graph is a graph for which there is at most one directed edge from
$(V_X, E_X)$
. On the other hand, a directed graph is a graph for which there is at most one directed edge from
![]() $v_i$
to
$v_i$
to
![]() $v_j$
. In this case, the set of edges is denoted
$v_j$
. In this case, the set of edges is denoted
![]() $E_X^+$
, and is a subset of
$E_X^+$
, and is a subset of
![]() $V_X\times V_X$
. More specifically, there is a directed edge joining
$V_X\times V_X$
. More specifically, there is a directed edge joining
![]() $v_i$
to
$v_i$
to
![]() $v_j$
precisely when
$v_j$
precisely when
![]() $(v_i, v_j)\in E_X^+$
. A multigraph is a graph with possibly multiple directed edges joining any two vertices, subject to some further conditions. In this case, the set
$(v_i, v_j)\in E_X^+$
. A multigraph is a graph with possibly multiple directed edges joining any two vertices, subject to some further conditions. In this case, the set
![]() $E_X^+$
is not a subset of
$E_X^+$
is not a subset of
![]() $V_X\times V_X$
, but simply admits a map to
$V_X\times V_X$
, but simply admits a map to
![]() $V_X\times V_X$
. The notion of a multigraph is more general than that of a graph. We give the precise definition below.
$V_X\times V_X$
. The notion of a multigraph is more general than that of a graph. We give the precise definition below.
Definition 2.1. A finite multigraph X is the data consisting of a finite set of vertices
![]() $V_X$
and a finite set of directed edges
$V_X$
and a finite set of directed edges
![]() $E_{X}^+$
along with functions:
$E_{X}^+$
along with functions:
 $$ \begin{align*}& i:E_{X}^{+} \to V_{X} \times V_{X},\\ &\iota:E_{X}^{+} \to E_{X}^{+}. \end{align*} $$
$$ \begin{align*}& i:E_{X}^{+} \to V_{X} \times V_{X},\\ &\iota:E_{X}^{+} \to E_{X}^{+}. \end{align*} $$
Here, i and
![]() $\iota $
are the incidence and inversion functions, respectively, and are subject to the following conditions:
$\iota $
are the incidence and inversion functions, respectively, and are subject to the following conditions:
-
1.
 $\iota ^{2} = \mathrm {id}_{E_{X}^{+}}$
,
$\iota ^{2} = \mathrm {id}_{E_{X}^{+}}$
, -
2.
 $\iota (e) \neq e$
for all
$\iota (e) \neq e$
for all
 $e \in E_{X}^{+}$
,
$e \in E_{X}^{+}$
, -
3.
 $i(\iota (e)) = \tau (i(e))$
for all
$i(\iota (e)) = \tau (i(e))$
for all
 $e \in E_{X}^{+}$
,
$e \in E_{X}^{+}$
,
where
![]() $\tau (x,y) := (y,x)$
.
$\tau (x,y) := (y,x)$
.
Given a directed edge
![]() $e\in E_X^+$
, the incidence function maps e to
$e\in E_X^+$
, the incidence function maps e to
![]() $i(e)=(v,v')$
. The edge starts at v and ends at the vertex
$i(e)=(v,v')$
. The edge starts at v and ends at the vertex
![]() $v'$
. We define functions
$v'$
. We define functions
![]() $o,t: E_X^+\rightarrow V_X$
, such that
$o,t: E_X^+\rightarrow V_X$
, such that
![]() $i(e)=(o(e), t(e))$
. In other words,
$i(e)=(o(e), t(e))$
. In other words,
![]() $o(e)$
(resp.
$o(e)$
(resp.
![]() $t(e)$
) is the projection of
$t(e)$
) is the projection of
![]() $i(e)$
to the first (resp. second) coordinate. We refer to the function o (resp. t) as the source (resp. target) function. The inversion map
$i(e)$
to the first (resp. second) coordinate. We refer to the function o (resp. t) as the source (resp. target) function. The inversion map
![]() $\iota $
satisfies the property that
$\iota $
satisfies the property that
![]() $i(\iota (e))=(t(e), o(e))$
. We shall occasionally denote the inverse
$i(\iota (e))=(t(e), o(e))$
. We shall occasionally denote the inverse
![]() $\iota (e)$
by
$\iota (e)$
by
![]() $\bar {e}$
. These two conventions will be used interchangeably throughout.
$\bar {e}$
. These two conventions will be used interchangeably throughout.
The set of directed edges e starting at a vertex v and ending at a vertex
![]() $v'$
are the edges which satisfy the relation
$v'$
are the edges which satisfy the relation
![]() $i(e)=(v,v')$
. We note that there may be any number of directed edges joining two vertices v and
$i(e)=(v,v')$
. We note that there may be any number of directed edges joining two vertices v and
![]() $v'$
, thus the graph X is referred to as a multigraph. We allow for there to be edges to start and end at the same vertex v, and such edges are referred to as loops based at v. We note that for distinct vertices v and
$v'$
, thus the graph X is referred to as a multigraph. We allow for there to be edges to start and end at the same vertex v, and such edges are referred to as loops based at v. We note that for distinct vertices v and
![]() $v'$
, there are as many directed edges starting at v and ending at
$v'$
, there are as many directed edges starting at v and ending at
![]() $v'$
as there are from
$v'$
as there are from
![]() $v'$
to v. Moreover, given a vertex v, there are an even number of directed loops starting and ending at v.
$v'$
to v. Moreover, given a vertex v, there are an even number of directed loops starting and ending at v.
Example. Let us illustrate the above definitions through an example. The set of vertices is
![]() $V_X=\{v_1, v_2\}$
. There are a total of six directed edges
$V_X=\{v_1, v_2\}$
. There are a total of six directed edges
![]() $E_X^+=\{a,b, c, \bar {a}, \bar {b}, \bar {c}\}$
, as depicted in the figure below.
$E_X^+=\{a,b, c, \bar {a}, \bar {b}, \bar {c}\}$
, as depicted in the figure below.

With respect to notation above,
![]() $i(a)=(v_1, v_1)$
,
$i(a)=(v_1, v_1)$
,
![]() $i(b)=i(c)=(v_1, v_2)$
.
$i(b)=i(c)=(v_1, v_2)$
.
2.2 Iwasawa theory of multigraphs
In this section, we discuss the Iwasawa theory of multigraphs. The basic object of study is a
![]() $\mathbb {Z}_\ell $
-tower of multigraphs. Let X be a multigraph. Recall from the previous section that the data associated with X consists of a finite set of vertices
$\mathbb {Z}_\ell $
-tower of multigraphs. Let X be a multigraph. Recall from the previous section that the data associated with X consists of a finite set of vertices
![]() $V_X=\{v_1, \dots , v_n\}$
and finitely many directed edges
$V_X=\{v_1, \dots , v_n\}$
and finitely many directed edges
![]() $E_X^+$
, along with an incidence map
$E_X^+$
, along with an incidence map
![]() $i:E_X^+\rightarrow V_X\times V_X$
, and an inversion map
$i:E_X^+\rightarrow V_X\times V_X$
, and an inversion map
![]() $\iota : E_X^+\rightarrow E_X^+$
. These maps are subject to further conditions. Before introducing
$\iota : E_X^+\rightarrow E_X^+$
. These maps are subject to further conditions. Before introducing
![]() $\mathbb {Z}_\ell $
-towers of multigraphs, we first discuss the notion of a Galois cover of multigraphs. For
$\mathbb {Z}_\ell $
-towers of multigraphs, we first discuss the notion of a Galois cover of multigraphs. For
![]() $v\in V_X$
, let
$v\in V_X$
, let
Let X and Y be two multigraphs. A morphism of graphs
![]() $f:Y \rightarrow X$
consists of two functions
$f:Y \rightarrow X$
consists of two functions
![]() $f_{V}:V_{Y} \rightarrow V_{X}$
and
$f_{V}:V_{Y} \rightarrow V_{X}$
and
![]() $f_{E}:E_{Y}^+ \rightarrow E_{X}^+$
satisfying:
$f_{E}:E_{Y}^+ \rightarrow E_{X}^+$
satisfying:
-
1.
 $f_{V}(o(e)) = o(f_{E}(e))$
,
$f_{V}(o(e)) = o(f_{E}(e))$
, -
2.
 $f_{V}(t(e)) = t(f_{E}(e))$
,
$f_{V}(t(e)) = t(f_{E}(e))$
, -
3.
 $\overline {f_{E}(e)} = f_{E}(\bar {e})$
,
$\overline {f_{E}(e)} = f_{E}(\bar {e})$
,
for all
![]() $e \in E_{X}^+$
. We will often write f for both
$e \in E_{X}^+$
. We will often write f for both
![]() $f_{V}$
and
$f_{V}$
and
![]() $f_{E}$
.
$f_{E}$
.
Definition 2.2. Let X and Y be two graphs, and let
![]() $f:Y\rightarrow X$
be a morphism of graphs. If f satisfies the following conditions:
$f:Y\rightarrow X$
be a morphism of graphs. If f satisfies the following conditions:
-
1.
 $f:V_{Y} \rightarrow V_{X}$
is surjective,
$f:V_{Y} \rightarrow V_{X}$
is surjective, -
2. for all
 $w \in V_{Y}$
, the restriction
$w \in V_{Y}$
, the restriction
 $f|_{E_{Y,w}}$
induces a bijection
$f|_{E_{Y,w}}$
induces a bijection  $$ \begin{align*}f|_{E_{Y,w}}:E_{Y,w} \stackrel{\approx}{\rightarrow}{E_{X,f(w)}},\end{align*} $$
$$ \begin{align*}f|_{E_{Y,w}}:E_{Y,w} \stackrel{\approx}{\rightarrow}{E_{X,f(w)}},\end{align*} $$
then f is said to be a cover.
If
![]() $Y/X$
is a cover and Y is connected, then there exists a positive integer d such that
$Y/X$
is a cover and Y is connected, then there exists a positive integer d such that
![]() $|f^{-1}(v)| = d$
for all
$|f^{-1}(v)| = d$
for all
![]() $v \in V_{X}$
. The integer d is called the degree of
$v \in V_{X}$
. The integer d is called the degree of
![]() $Y/X$
and will be denoted by
$Y/X$
and will be denoted by
![]() $[Y:X]$
. If
$[Y:X]$
. If
![]() $f:Y \rightarrow X$
is a cover, then we let
$f:Y \rightarrow X$
is a cover, then we let
Definition 2.3. The cover
![]() $f:Y \rightarrow X$
is called Galois if the following two conditions are satisfied.
$f:Y \rightarrow X$
is called Galois if the following two conditions are satisfied.
-
1. The graphs X and Y are connected.
-
2. The group
 $\mathrm {Aut}_{f}(Y/X)$
acts transitively on the fiber
$\mathrm {Aut}_{f}(Y/X)$
acts transitively on the fiber
 $f^{-1}(v)$
for all
$f^{-1}(v)$
for all
 $v \in V_{X}$
.
$v \in V_{X}$
.
If
![]() $Y/X$
is a Galois cover, then
$Y/X$
is a Galois cover, then
![]() $[Y:X] = |\mathrm {Aut}_{f}(Y/X)|$
, and we write
$[Y:X] = |\mathrm {Aut}_{f}(Y/X)|$
, and we write
![]() $\mathrm {Gal}_{f}(Y/X)$
, or
$\mathrm {Gal}_{f}(Y/X)$
, or
![]() $\mathrm {Gal}(Y/X)$
if f is understood, instead of
$\mathrm {Gal}(Y/X)$
if f is understood, instead of
![]() $\mathrm {Aut}_{f}(Y/X)$
. One has the usual Galois correspondence between subgroups of
$\mathrm {Aut}_{f}(Y/X)$
. One has the usual Galois correspondence between subgroups of
![]() $\mathrm {Gal}(Y/X)$
and equivalence classes of intermediate covers of
$\mathrm {Gal}(Y/X)$
and equivalence classes of intermediate covers of
![]() $Y/X$
.
$Y/X$
.
Galois covers of a multigraph can be constructed from certain combinatorial data associated with a multigraph, as we now explain. Define an equivalence relation on
![]() $E_X^+$
, by setting
$E_X^+$
, by setting
![]() $e\sim e'$
if
$e\sim e'$
if
![]() $e=e'$
or
$e=e'$
or
![]() $e=\bar {e}'$
. The set of equivalence classes
$e=\bar {e}'$
. The set of equivalence classes
![]() $E_X:=E_X^+/\iota $
is the set of undirected edges, and let
$E_X:=E_X^+/\iota $
is the set of undirected edges, and let
![]() $\pi :E_X^+\to E_{X}$
be the
$\pi :E_X^+\to E_{X}$
be the
![]() $2:1$
natural quotient map, mapping a directed edge to the associated undirected edge. Choose a section
$2:1$
natural quotient map, mapping a directed edge to the associated undirected edge. Choose a section
![]() $\gamma :E_{X} \to E_{X}^+$
to
$\gamma :E_{X} \to E_{X}^+$
to
![]() $\pi $
, and set
$\pi $
, and set
![]() $S:=\gamma (E_{X})$
. Our main reference for voltage assignments and derived multigraphs is [Reference Gross and Tucker9], but we rephrase everything in the formalism used in [Reference Sunada24].
$S:=\gamma (E_{X})$
. Our main reference for voltage assignments and derived multigraphs is [Reference Gross and Tucker9], but we rephrase everything in the formalism used in [Reference Sunada24].
Definition 2.4. Let G be a finite abelian group. With respect to notation above, a voltage assignment is a function
![]() $\alpha :S \to G$
.
$\alpha :S \to G$
.
We extend
![]() $\alpha $
to all of
$\alpha $
to all of
![]() $E_{X}^{+}$
by setting
$E_{X}^{+}$
by setting
![]() $\alpha (\bar {s}) = \alpha (s)^{-1}$
. To this data, one can associate a multigraph
$\alpha (\bar {s}) = \alpha (s)^{-1}$
. To this data, one can associate a multigraph
![]() $X(G,S,\alpha )$
as follows. The set of vertices is
$X(G,S,\alpha )$
as follows. The set of vertices is
![]() $V = V_{X} \times G$
and the set of directed edges is
$V = V_{X} \times G$
and the set of directed edges is
![]() $E^{+} = E_{X}^{+} \times G$
. The directed edge
$E^{+} = E_{X}^{+} \times G$
. The directed edge
![]() $(e,\sigma )$
connects
$(e,\sigma )$
connects
![]() $(o(e),\sigma )$
to
$(o(e),\sigma )$
to
![]() $(t(e),\sigma \cdot \alpha (e))$
(where we recall that
$(t(e),\sigma \cdot \alpha (e))$
(where we recall that
![]() $o(e)$
and
$o(e)$
and
![]() $t(e)$
denote the origin and the target of the edge e, respectively), and the inversion map is given by
$t(e)$
denote the origin and the target of the edge e, respectively), and the inversion map is given by
If
![]() $G_{1}$
is another finite abelian group and
$G_{1}$
is another finite abelian group and
![]() $f:G \to G_{1}$
is a group morphism, then one obtains a morphism of multigraphs
$f:G \to G_{1}$
is a group morphism, then one obtains a morphism of multigraphs
![]() $f_{*}:X(G,S,\alpha ) \to X(G_{1},S,f \circ \alpha )$
that is defined via
$f_{*}:X(G,S,\alpha ) \to X(G_{1},S,f \circ \alpha )$
that is defined via
If both
![]() $X(G,S,\alpha )$
and
$X(G,S,\alpha )$
and
![]() $X(G,S,f \circ \alpha )$
are connected and f is surjective, then
$X(G,S,f \circ \alpha )$
are connected and f is surjective, then
![]() $f_{*}$
is a cover in the sense of Definition 2.2 and in fact is a Galois cover with group of covering transformations isomorphic to
$f_{*}$
is a cover in the sense of Definition 2.2 and in fact is a Galois cover with group of covering transformations isomorphic to
![]() $\mathrm {ker}(f)$
. In particular, if
$\mathrm {ker}(f)$
. In particular, if
![]() $f:G \to \{ 1\}$
is the group morphism into the trivial group and both X and
$f:G \to \{ 1\}$
is the group morphism into the trivial group and both X and
![]() $X(G,S,\alpha )$
are connected, then we get a Galois cover
$X(G,S,\alpha )$
are connected, then we get a Galois cover
![]() $f_{*}:X(G,S,\alpha ) \to X$
with group of covering transformation isomorphic to G.
$f_{*}:X(G,S,\alpha ) \to X$
with group of covering transformation isomorphic to G.
We now recall the notion of a
![]() $\mathbb {Z}_\ell $
-tower of multigraphs.
$\mathbb {Z}_\ell $
-tower of multigraphs.
Definition 2.5. Let
![]() $\ell $
be a rational prime, and let X be a connected graph. A
$\ell $
be a rational prime, and let X be a connected graph. A
![]() $\mathbb {Z}_{\ell }$
-tower above X consists of a sequence of covers of connected graphs
$\mathbb {Z}_{\ell }$
-tower above X consists of a sequence of covers of connected graphs
such that for all positive integer n, the cover
![]() $X_{n}/X$
obtained from composing the covers
$X_{n}/X$
obtained from composing the covers
![]() $X_{n} \rightarrow X_{n-1} \rightarrow \cdots \rightarrow X_{1} \rightarrow X$
is Galois with Galois group
$X_{n} \rightarrow X_{n-1} \rightarrow \cdots \rightarrow X_{1} \rightarrow X$
is Galois with Galois group
![]() $\mathrm {Gal}(X_{n}/X)$
isomorphic to
$\mathrm {Gal}(X_{n}/X)$
isomorphic to
![]() $\mathbb {Z}/\ell ^{n}\mathbb {Z}$
.
$\mathbb {Z}/\ell ^{n}\mathbb {Z}$
.
We specialize the above construction to the case when
![]() $G=\mathbb {Z}_\ell $
. Set
$G=\mathbb {Z}_\ell $
. Set
![]() $\alpha _{/n}$
to denote the mod-
$\alpha _{/n}$
to denote the mod-
![]() $\ell ^n$
reduction of
$\ell ^n$
reduction of
![]() $\alpha $
. We obtain a
$\alpha $
. We obtain a
![]() $\mathbb {Z}_{\ell }$
-tower above X:
$\mathbb {Z}_{\ell }$
-tower above X:
Set
![]() $t:=|S|$
and enumerate
$t:=|S|$
and enumerate
![]() $S=\{s_1,\dots , s_t\}$
, and let
$S=\{s_1,\dots , s_t\}$
, and let
![]() $\alpha _i$
denote
$\alpha _i$
denote
![]() $\alpha (s_i)$
. We may view
$\alpha (s_i)$
. We may view
![]() $\alpha $
as a vector
$\alpha $
as a vector
![]() $\alpha =(\alpha _1, \alpha _2,\dots , \alpha _t)\in \mathbb {Z}_\ell ^t$
. The following assumption on the multigraphs
$\alpha =(\alpha _1, \alpha _2,\dots , \alpha _t)\in \mathbb {Z}_\ell ^t$
. The following assumption on the multigraphs
![]() $X(\mathbb {Z}/\ell ^n \mathbb {Z}, S, \alpha _{/n})$
is necessary to relate the growth patterns in Picard groups to Iwasawa invariants. In §2.3, we introduce conditions under which the following assumption is satisfied.
$X(\mathbb {Z}/\ell ^n \mathbb {Z}, S, \alpha _{/n})$
is necessary to relate the growth patterns in Picard groups to Iwasawa invariants. In §2.3, we introduce conditions under which the following assumption is satisfied.
Assumptions 2.6. Let
![]() $\ell $
be a prime (with
$\ell $
be a prime (with
![]() $\ell =2$
allowed), and let
$\ell =2$
allowed), and let
![]() $\alpha : S\rightarrow \mathbb {Z}_\ell $
be a function. We assume that the derived multigraphs
$\alpha : S\rightarrow \mathbb {Z}_\ell $
be a function. We assume that the derived multigraphs
![]() $X(\mathbb {Z}/\ell ^n \mathbb {Z}, S, \alpha _{/n})$
are connected for all
$X(\mathbb {Z}/\ell ^n \mathbb {Z}, S, \alpha _{/n})$
are connected for all
![]() $n\geq 0$
.
$n\geq 0$
.
Examples. Let us illustrate the above construction of a
![]() $\mathbb {Z}_\ell $
-tower through some explicit examples.
$\mathbb {Z}_\ell $
-tower through some explicit examples.
-
1. Let X be a bouquet with two loops, and choose an orientation
 $S =\{s_{1}, s_{2} \}$
of
$S =\{s_{1}, s_{2} \}$
of
 $E_{X}^{+}$
. Let
$E_{X}^{+}$
. Let
 $\ell = 3$
, and consider the function
$\ell = 3$
, and consider the function
 $\alpha :E_{X}^{+} \rightarrow \mathbb {Z} \subseteq \mathbb {Z}_{3}$
given by By Corollary 2.16, all the graphs
$\alpha :E_{X}^{+} \rightarrow \mathbb {Z} \subseteq \mathbb {Z}_{3}$
given by By Corollary 2.16, all the graphs $$ \begin{align*}s_{1} \mapsto \alpha(s_{1}) = 1 \text{ and } s_{2} \mapsto \alpha(s_{2}) = 11.\end{align*} $$
$$ \begin{align*}s_{1} \mapsto \alpha(s_{1}) = 1 \text{ and } s_{2} \mapsto \alpha(s_{2}) = 11.\end{align*} $$
 $X(\mathbb {Z}/3^{n}\mathbb {Z},S,\alpha _{/n})$
are connected. We obtain a
$X(\mathbb {Z}/3^{n}\mathbb {Z},S,\alpha _{/n})$
are connected. We obtain a
 $\mathbb {Z}_{3}$
-tower above the bouquet graph X which can be pictured as follows:
$\mathbb {Z}_{3}$
-tower above the bouquet graph X which can be pictured as follows:
-
2. Let
 $\ell =3$
again, and let now X be the dumbbell multigraph
$\ell =3$
again, and let now X be the dumbbell multigraph
the section be

and take the function
 $\alpha :S \rightarrow \mathbb {Z} \subseteq \mathbb {Z}_{3}$
given by By Theorem 2.15, all the multigraphs
$\alpha :S \rightarrow \mathbb {Z} \subseteq \mathbb {Z}_{3}$
given by By Theorem 2.15, all the multigraphs $$ \begin{align*}s_{1} \mapsto \alpha(s_{1}) = 1, s_{2} \mapsto \alpha(s_{2}) =0, \text{ and } s_{3} \mapsto \alpha(s_{3}) = 11.\end{align*} $$
$$ \begin{align*}s_{1} \mapsto \alpha(s_{1}) = 1, s_{2} \mapsto \alpha(s_{2}) =0, \text{ and } s_{3} \mapsto \alpha(s_{3}) = 11.\end{align*} $$
 $X(\mathbb {Z}/3^{n}\mathbb {Z},S,\alpha _{/n})$
are connected. We obtain a
$X(\mathbb {Z}/3^{n}\mathbb {Z},S,\alpha _{/n})$
are connected. We obtain a
 $\mathbb {Z}_{3}$
-tower above the dumbbell multigraph X which can be pictured as follows:
$\mathbb {Z}_{3}$
-tower above the dumbbell multigraph X which can be pictured as follows:
Note that the graphs
 $X(\mathbb {Z}/3^{n}\mathbb {Z},S,\alpha _{/n})$
are precisely the generalized Petersen graphs
$X(\mathbb {Z}/3^{n}\mathbb {Z},S,\alpha _{/n})$
are precisely the generalized Petersen graphs
 $G(3^{n},11)$
.
$G(3^{n},11)$
.
Let
![]() $u_X$
be the number of vertices of X and label
$u_X$
be the number of vertices of X and label
![]() $V_X=\{v_1,\dots , v_{u_X}\}$
. Let
$V_X=\{v_1,\dots , v_{u_X}\}$
. Let
![]() $o,t: E_X^+\rightarrow V_X$
be the origin and terminus functions taking an edge to its source and target vertex, respectively. Thus, we have that
$o,t: E_X^+\rightarrow V_X$
be the origin and terminus functions taking an edge to its source and target vertex, respectively. Thus, we have that
![]() $i(e)=(o(e), t(e))$
. For
$i(e)=(o(e), t(e))$
. For
![]() $v\in V_X$
, set
$v\in V_X$
, set
![]() $E_v:=\{e\in E_X^+\mid o(e)=v\}$
, and let
$E_v:=\{e\in E_X^+\mid o(e)=v\}$
, and let
![]() $\operatorname {val}_X(v):=\# E_v$
be the valency of v. The divisor group
$\operatorname {val}_X(v):=\# E_v$
be the valency of v. The divisor group
![]() $\operatorname {Div}(X)$
is the free abelian group on the vertices
$\operatorname {Div}(X)$
is the free abelian group on the vertices
![]() $V_X$
of X. It consists of formal sums of the form
$V_X$
of X. It consists of formal sums of the form
![]() $D=\sum _{v\in V_X} n_v v$
, where
$D=\sum _{v\in V_X} n_v v$
, where
![]() $n_v\in \mathbb {Z}$
for all v. The degree of D is the sum
$n_v\in \mathbb {Z}$
for all v. The degree of D is the sum
![]() $\operatorname {deg}(D):=\sum _v n_v\in \mathbb {Z}$
, and this defines a homomorphism
$\operatorname {deg}(D):=\sum _v n_v\in \mathbb {Z}$
, and this defines a homomorphism
the kernel of which is denoted
![]() $\operatorname {Div}^0(X)$
. Let
$\operatorname {Div}^0(X)$
. Let
![]() $\mathcal {M}(X)$
be the abelian group of
$\mathcal {M}(X)$
be the abelian group of
![]() $\mathbb {Z}$
-valued functions on
$\mathbb {Z}$
-valued functions on
![]() $V_X$
. The discrete Laplacian map
$V_X$
. The discrete Laplacian map
![]() $\mathrm {div}:\mathcal {M}(X) \to \mathrm {Div}(X)$
is defined as follows. For
$\mathrm {div}:\mathcal {M}(X) \to \mathrm {Div}(X)$
is defined as follows. For
![]() $f \in \mathcal {M}(X)$
, one sets
$f \in \mathcal {M}(X)$
, one sets
where
 $$ \begin{align*}{m_{v}(f)} = \sum_{e \in E_{X,v}}\left(f(t(e)) - f(o(e))\right).\end{align*} $$
$$ \begin{align*}{m_{v}(f)} = \sum_{e \in E_{X,v}}\left(f(t(e)) - f(o(e))\right).\end{align*} $$
We let
![]() $\operatorname {Pr}(X)$
be the image of
$\operatorname {Pr}(X)$
be the image of
![]() $\operatorname {div}$
. It is easy to see that
$\operatorname {div}$
. It is easy to see that
![]() $\operatorname {Pr}(X)$
is a subgroup of
$\operatorname {Pr}(X)$
is a subgroup of
![]() $\operatorname {Div}^0(X)$
, since the subjacent directed graph is Eulerian, meaning that every vertex has in-degree equals to its out-degree. The Picard group is taken to be the quotient
$\operatorname {Div}^0(X)$
, since the subjacent directed graph is Eulerian, meaning that every vertex has in-degree equals to its out-degree. The Picard group is taken to be the quotient
![]() $\operatorname {Pic}(X):=\operatorname {Div}(X)/\operatorname {Pr}(X)$
, and we set
$\operatorname {Pic}(X):=\operatorname {Div}(X)/\operatorname {Pr}(X)$
, and we set
![]() $\operatorname {Pic}^0(X):=\operatorname {Div}^0(X)/\operatorname {Pr}(X)$
. Set
$\operatorname {Pic}^0(X):=\operatorname {Div}^0(X)/\operatorname {Pr}(X)$
. Set
![]() $\kappa _X$
to be the cardinality of
$\kappa _X$
to be the cardinality of
![]() $\operatorname {Pic}^0(X)$
, which is a finite group and is equal to the number of spanning trees in X.
$\operatorname {Pic}^0(X)$
, which is a finite group and is equal to the number of spanning trees in X.
The valency matrix is the
![]() $u_X\times u_X$
diagonal matrix
$u_X\times u_X$
diagonal matrix
![]() $D=(d_{i,j})$
, with
$D=(d_{i,j})$
, with
 $$\begin{align*}d_{i,j}=\begin{cases} \operatorname{val}_X(v_i), & \text{ for }i=j,\\ 0, & \text{ for }i\neq j. \end{cases}\end{align*}$$
$$\begin{align*}d_{i,j}=\begin{cases} \operatorname{val}_X(v_i), & \text{ for }i=j,\\ 0, & \text{ for }i\neq j. \end{cases}\end{align*}$$
The adjacency matrix
![]() $A=(a_{i,j})$
is given by
$A=(a_{i,j})$
is given by
 $$\begin{align*}a_{i,j}=\begin{cases} \text{Twice the number of undirected loops at }i,\text{ } & i=j,\\ \text{The number of undirected edges connecting the }i\text{th and }j\text{th vertices}, & i\neq j. \end{cases}\end{align*}$$
$$\begin{align*}a_{i,j}=\begin{cases} \text{Twice the number of undirected loops at }i,\text{ } & i=j,\\ \text{The number of undirected edges connecting the }i\text{th and }j\text{th vertices}, & i\neq j. \end{cases}\end{align*}$$
The matrix
![]() $Q:=D-A$
is called the Laplacian matrix.
$Q:=D-A$
is called the Laplacian matrix.
We let
![]() $\mathbb {Z}_\ell [x]$
(resp.
$\mathbb {Z}_\ell [x]$
(resp. ![]() ) denote the polynomial ring (resp. formal power series ring) in the indeterminate x (resp. T) with coefficients in
) denote the polynomial ring (resp. formal power series ring) in the indeterminate x (resp. T) with coefficients in
![]() $\mathbb {Z}_\ell $
. Denote by
$\mathbb {Z}_\ell $
. Denote by
![]() $\mathbb {Z}_\ell [x;\mathbb {Z}_\ell ]$
the ring whose elements are expressions of the form
$\mathbb {Z}_\ell [x;\mathbb {Z}_\ell ]$
the ring whose elements are expressions of the form
![]() $f(x)=\sum _{a} c_a x^a$
, where a runs over a finite set in
$f(x)=\sum _{a} c_a x^a$
, where a runs over a finite set in
![]() $\mathbb {Z}_\ell $
and the coefficient
$\mathbb {Z}_\ell $
and the coefficient
![]() $c_a$
is in
$c_a$
is in
![]() $\mathbb {Z}_\ell $
. Here, multiplication is defined by setting
$\mathbb {Z}_\ell $
. Here, multiplication is defined by setting
![]() $x^ax^b=x^{a+b}$
for
$x^ax^b=x^{a+b}$
for
![]() $a,b\in \mathbb {Z}_\ell $
. Associate a matrix
$a,b\in \mathbb {Z}_\ell $
. Associate a matrix
![]() $M(x)$
to the pair
$M(x)$
to the pair
![]() $(X,\alpha )$
as follows:
$(X,\alpha )$
as follows:
 $$ \begin{align}M(x)=M_{X,\alpha}(x):=D - \left(\sum_{\substack{s \in S \\ {i}(s) = (v_{i},v_{j})}} x^{\alpha(s)} + \sum_{\substack{s \in S \\ { i}(s) = (v_{j},v_{i})}} x^{-\alpha(s)} \right) \in M_{u \times u}(\mathbb{Z}[x;\mathbb{Z}_{\ell}]).\end{align} $$
$$ \begin{align}M(x)=M_{X,\alpha}(x):=D - \left(\sum_{\substack{s \in S \\ {i}(s) = (v_{i},v_{j})}} x^{\alpha(s)} + \sum_{\substack{s \in S \\ { i}(s) = (v_{j},v_{i})}} x^{-\alpha(s)} \right) \in M_{u \times u}(\mathbb{Z}[x;\mathbb{Z}_{\ell}]).\end{align} $$
For
![]() $b\in \mathbb {Z}_\ell $
, let
$b\in \mathbb {Z}_\ell $
, let
![]() ${b\choose n}\in \mathbb {Z}_\ell $
be given by
${b\choose n}\in \mathbb {Z}_\ell $
be given by
 $$\begin{align*}{b\choose n}:=\frac{b(b-1)\dots (b-n+1)}{n!}.\end{align*}$$
$$\begin{align*}{b\choose n}:=\frac{b(b-1)\dots (b-n+1)}{n!}.\end{align*}$$
Let
![]() $(1+T)^b$
be the formal power series
$(1+T)^b$
be the formal power series
 $$\begin{align*}(1+T)^b:=\sum_{n=0}^\infty {b\choose n} T^n.\end{align*}$$
$$\begin{align*}(1+T)^b:=\sum_{n=0}^\infty {b\choose n} T^n.\end{align*}$$
With this convention in place, we define the characteristic series to be
which is a formal power series in ![]() . The convention used in this article differs from that used in [Reference McGown and Vallières20], where
. The convention used in this article differs from that used in [Reference McGown and Vallières20], where
![]() $-T$
is used in place of T. This convention simplifies our calculations.
$-T$
is used in place of T. This convention simplifies our calculations.
Lemma 2.7. Let X be a multigraph,
![]() $\ell $
be a prime and
$\ell $
be a prime and
![]() $\alpha :S\rightarrow \mathbb {Z}_\ell $
a function. The constant term of the characteristic series
$\alpha :S\rightarrow \mathbb {Z}_\ell $
a function. The constant term of the characteristic series
![]() $f(T)$
(see (2.2)) is equal to
$f(T)$
(see (2.2)) is equal to
![]() $0$
.
$0$
.
Proof. Note that the constant term of
![]() $f(T)$
is
$f(T)$
is
![]() $\operatorname {det}(Q)$
. The vector
$\operatorname {det}(Q)$
. The vector
![]() $(1,\ldots ,1)^t$
is in the null-space of Q (see [Reference Corry and Perkinson1, proof of Cor. 9.10] for further details). Therefore, Q is singular and the result follows.
$(1,\ldots ,1)^t$
is in the null-space of Q (see [Reference Corry and Perkinson1, proof of Cor. 9.10] for further details). Therefore, Q is singular and the result follows.
The following result shows that
![]() $f_{X, \alpha }(T)\neq 0$
under the assumptions imposed on
$f_{X, \alpha }(T)\neq 0$
under the assumptions imposed on
![]() $\alpha $
. The proof is essentially contained in [Reference McGown and Vallières19], [Reference McGown and Vallières20], and [26], we recall these details. First, we introduce some further notation. Let
$\alpha $
. The proof is essentially contained in [Reference McGown and Vallières19], [Reference McGown and Vallières20], and [26], we recall these details. First, we introduce some further notation. Let
![]() $Y/X$
be an abelian cover of multigraphs and set
$Y/X$
be an abelian cover of multigraphs and set
![]() $G:=\operatorname {Gal}(Y/X)$
. Let
$G:=\operatorname {Gal}(Y/X)$
. Let
![]() $\widehat {G}$
be the group of characters
$\widehat {G}$
be the group of characters
![]() $\psi : G\rightarrow \mathbb {C}^\times $
. Given
$\psi : G\rightarrow \mathbb {C}^\times $
. Given
![]() $\psi \in \widehat {G}$
, denote the Artin–Ihara L-function by
$\psi \in \widehat {G}$
, denote the Artin–Ihara L-function by
 $$\begin{align*}L_X(z, \psi):=\prod_{\mathfrak{c}}\left(1-\psi\left(\left(\frac{Y/X}{\frak{c}}\right)\right)z^{l(\mathfrak{c})}\right)^{-1}.\end{align*}$$
$$\begin{align*}L_X(z, \psi):=\prod_{\mathfrak{c}}\left(1-\psi\left(\left(\frac{Y/X}{\frak{c}}\right)\right)z^{l(\mathfrak{c})}\right)^{-1}.\end{align*}$$
Here, the product runs over all primes
![]() $\mathfrak {c}$
of X,
$\mathfrak {c}$
of X,
![]() $l(\mathfrak {c})$
is the length of
$l(\mathfrak {c})$
is the length of
![]() $\mathfrak {c}$
and
$\mathfrak {c}$
and
![]() $\left (\frac {Y/X}{\frak {c}}\right )$
is the Frobenius automorphism at
$\left (\frac {Y/X}{\frak {c}}\right )$
is the Frobenius automorphism at
![]() $\mathfrak {c}$
. (Recall that a prime in a multigraph is an equivalence class of closed paths that have no backtrack or tail, and that are not multiples of a strictly smaller closed path, where two such paths are identified if they are the same up to their starting vertex. For further details, the reader is referred to [Reference Terras25, Ch. 18].) Let
$\mathfrak {c}$
. (Recall that a prime in a multigraph is an equivalence class of closed paths that have no backtrack or tail, and that are not multiples of a strictly smaller closed path, where two such paths are identified if they are the same up to their starting vertex. For further details, the reader is referred to [Reference Terras25, Ch. 18].) Let
![]() $\chi (X)$
denote the Euler characteristic of X, which is defined as follows:
$\chi (X)$
denote the Euler characteristic of X, which is defined as follows:
We shall impose the following assumption without further mention.
Assumptions 2.8. Throughout, we assume that
![]() $\chi (X)\neq 0$
.
$\chi (X)\neq 0$
.
That
![]() $\chi (X)\neq 0$
means that X does not consist of a single cycle, or a “cycle with hair,” compare [Reference Terras25, Fig. 2.1]. When
$\chi (X)\neq 0$
means that X does not consist of a single cycle, or a “cycle with hair,” compare [Reference Terras25, Fig. 2.1]. When
![]() $\chi (X)=0$
, X is referred to as a “bad graph,” compare [Reference Terras25] (and the references therein), since many arithmetic properties of zeta functions are not satisfied in this case. For instance, the analog of the prime number theorem for such bad graphs does not hold, compare [Reference Terras25, Th. 10.1].
$\chi (X)=0$
, X is referred to as a “bad graph,” compare [Reference Terras25] (and the references therein), since many arithmetic properties of zeta functions are not satisfied in this case. For instance, the analog of the prime number theorem for such bad graphs does not hold, compare [Reference Terras25, Th. 10.1].
Definition 2.9. Let
![]() $Y/X$
be an abelian cover of multigraphs with automorphism group G, and for each
$Y/X$
be an abelian cover of multigraphs with automorphism group G, and for each
![]() $i=1,\ldots ,u_{X}$
, let
$i=1,\ldots ,u_{X}$
, let
![]() $w_{i}$
be a fixed vertex in the fiber of
$w_{i}$
be a fixed vertex in the fiber of
![]() $v_{i}$
.
$v_{i}$
.
-
1. For
 $\sigma \in G$
, we let the matrix
$\sigma \in G$
, we let the matrix
 $A(\sigma )$
to be the
$A(\sigma )$
to be the
 $u_{X} \times u_{X}$
matrix
$u_{X} \times u_{X}$
matrix
 $A(\sigma )=(a_{i,j}(\sigma ))$
defined via
$A(\sigma )=(a_{i,j}(\sigma ))$
defined via  $$ \begin{align*} a_{i,j}(\sigma) = \begin{cases} \text{Twice the number of undirected loops at }w_{i}, &\text{ if } i=j \text{ and } \sigma = 1,\\ \text{The number of undirected edges connecting }w_{i}\text{ to }w_{j}^{\sigma}, &\text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} a_{i,j}(\sigma) = \begin{cases} \text{Twice the number of undirected loops at }w_{i}, &\text{ if } i=j \text{ and } \sigma = 1,\\ \text{The number of undirected edges connecting }w_{i}\text{ to }w_{j}^{\sigma}, &\text{ otherwise}. \end{cases} \end{align*} $$
-
2. For
 $\psi \in \widehat {G}$
, we set
$\psi \in \widehat {G}$
, we set  $$ \begin{align*}A_{\psi} = \sum_{\sigma \in G} \psi(\sigma) \cdot A(\sigma).\end{align*} $$
$$ \begin{align*}A_{\psi} = \sum_{\sigma \in G} \psi(\sigma) \cdot A(\sigma).\end{align*} $$
Lemma 2.10. Let
![]() $\alpha :S\to \mathbb {Z}_{\ell }$
be a function for which Assumption 2.6 is satisfied, then
$\alpha :S\to \mathbb {Z}_{\ell }$
be a function for which Assumption 2.6 is satisfied, then
![]() $f_{X,\alpha }(T) \neq 0$
.
$f_{X,\alpha }(T) \neq 0$
.
Proof. The relationship between the power series
![]() $Q(T)$
of [Reference McGown and Vallières20, Th. 6.1] and
$Q(T)$
of [Reference McGown and Vallières20, Th. 6.1] and
![]() $f_{X,\alpha }(T)$
is
$f_{X,\alpha }(T)$
is
![]() $Q(T) = f_{X,\alpha }(-T)$
. If
$Q(T) = f_{X,\alpha }(-T)$
. If
![]() $Y/X$
is an abelian cover of multigraphs and
$Y/X$
is an abelian cover of multigraphs and
![]() $\psi $
is a character of
$\psi $
is a character of
![]() $G = \mathrm {Gal}(Y/X)$
, then the three-term determinant formula [Reference Terras25, Th. 18.15] for the Artin–Ihara L-function gives
$G = \mathrm {Gal}(Y/X)$
, then the three-term determinant formula [Reference Terras25, Th. 18.15] for the Artin–Ihara L-function gives
where
![]() $A_{\psi }$
is the twisted adjacency matrix of Definition 2.9, D is the valency matrix of X, and
$A_{\psi }$
is the twisted adjacency matrix of Definition 2.9, D is the valency matrix of X, and
![]() $\chi (X)$
is the Euler characteristic of X. From now on, we let
$\chi (X)$
is the Euler characteristic of X. From now on, we let
Coming back to the abelian
![]() $\ell $
-tower
$\ell $
-tower
associated with
![]() $\alpha $
, for all positive integer n, [Reference McGown and Vallières20, Cor. 5.6] implies
$\alpha $
, for all positive integer n, [Reference McGown and Vallières20, Cor. 5.6] implies
where
![]() $\psi _{n}$
is the character of
$\psi _{n}$
is the character of
![]() $\mathbb {Z}/\ell ^{n}\mathbb {Z} \simeq \mathrm {Gal}(X(\mathbb {Z}/\ell ^{n}\mathbb {Z},S,\alpha _{/n})/X)$
satisfying
$\mathbb {Z}/\ell ^{n}\mathbb {Z} \simeq \mathrm {Gal}(X(\mathbb {Z}/\ell ^{n}\mathbb {Z},S,\alpha _{/n})/X)$
satisfying
![]() $\psi _{n}(\bar {1}) = \zeta _{\ell ^{n}}$
. Here, it is understood that
$\psi _{n}(\bar {1}) = \zeta _{\ell ^{n}}$
. Here, it is understood that
![]() $\zeta _{\ell ^{n}} = \exp (2 \pi i/\ell ^{n})$
and that an embedding of
$\zeta _{\ell ^{n}} = \exp (2 \pi i/\ell ^{n})$
and that an embedding of
![]() $\overline {\mathbb {Q}}$
into
$\overline {\mathbb {Q}}$
into
![]() $\overline {\mathbb {Q}}_{\ell }$
has been fixed once and for all so that we view
$\overline {\mathbb {Q}}_{\ell }$
has been fixed once and for all so that we view
![]() $\zeta _{\ell ^{n}}$
and the values of the characters
$\zeta _{\ell ^{n}}$
and the values of the characters
![]() $\psi _{n}$
inside
$\psi _{n}$
inside
![]() $\overline {\mathbb {Q}}_{\ell }$
. From [Reference Vallières26, Sec. 3], one has
$\overline {\mathbb {Q}}_{\ell }$
. From [Reference Vallières26, Sec. 3], one has
 $$ \begin{align*}\ell^{n} \cdot \kappa_{n} = \kappa_{X} \cdot \prod_{\psi \neq \psi_{0}} h_{X}(1,\psi),\end{align*} $$
$$ \begin{align*}\ell^{n} \cdot \kappa_{n} = \kappa_{X} \cdot \prod_{\psi \neq \psi_{0}} h_{X}(1,\psi),\end{align*} $$
where the product is over all nontrivial characters of
![]() $\mathbb {Z}/\ell ^{n}\mathbb {Z}$
, and
$\mathbb {Z}/\ell ^{n}\mathbb {Z}$
, and
![]() $\kappa _n$
denotes the number of spanning trees of
$\kappa _n$
denotes the number of spanning trees of
![]() $X(\mathbb {Z}/\ell ^{n}\mathbb {Z},S,\alpha _{/n})$
. The above formula crucially requires the Assumption 2.8. It follows that
$X(\mathbb {Z}/\ell ^{n}\mathbb {Z},S,\alpha _{/n})$
. The above formula crucially requires the Assumption 2.8. It follows that
for all nontrivial characters, and thus
![]() $Q(T) \neq 0$
by (2.3).
$Q(T) \neq 0$
by (2.3).
Associated with the characteristic series, are the Iwasawa
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
invariants, which we now proceed to define. A polynomial is said to be a distinguished polynomial if it is monic and all non-leading coefficients are divisible by
$\lambda $
invariants, which we now proceed to define. A polynomial is said to be a distinguished polynomial if it is monic and all non-leading coefficients are divisible by
![]() $\ell $
.
$\ell $
.
Definition 2.11. By the Weierstrass Preparation theorem, we may factor the characteristic polynomial as follows:
![]() $f(T)=\ell ^{\mu } g(T) u(T)$
, where
$f(T)=\ell ^{\mu } g(T) u(T)$
, where
![]() $g(T)$
is a distinguished polynomial in
$g(T)$
is a distinguished polynomial in ![]() , and
, and
![]() $u(T)$
is a unit in
$u(T)$
is a unit in ![]() . Since
. Since
![]() $u(T)$
is a unit in
$u(T)$
is a unit in ![]() , the constant term
, the constant term
![]() $u(0)$
is a unit in
$u(0)$
is a unit in
![]() $\mathbb {Z}_\ell $
. According to Lemma 2.7, the constant term of
$\mathbb {Z}_\ell $
. According to Lemma 2.7, the constant term of
![]() $f(T)$
is equal to
$f(T)$
is equal to
![]() $0$
, and hence, T divides
$0$
, and hence, T divides
![]() $g(T)$
. In particular, we have that
$g(T)$
. In particular, we have that
![]() $\operatorname {deg} g\geq 1$
. The number
$\operatorname {deg} g\geq 1$
. The number
![]() $\mu \in \mathbb {Z}_{\geq 0}$
is the
$\mu \in \mathbb {Z}_{\geq 0}$
is the
![]() $\mu $
-invariant and depends on
$\mu $
-invariant and depends on
![]() $(\ell ,\alpha )$
. Throughout, it is assumed that Assumption 2.6 is satisfied for
$(\ell ,\alpha )$
. Throughout, it is assumed that Assumption 2.6 is satisfied for
![]() $\alpha $
. Thus, we denote this invariant by
$\alpha $
. Thus, we denote this invariant by
![]() $\mu _{\ell }(X,\alpha )$
, however, when
$\mu _{\ell }(X,\alpha )$
, however, when
![]() $\ell $
, X and
$\ell $
, X and
![]() $\alpha :S\rightarrow \mathbb {Z}_\ell $
are understood, we simply denote it by
$\alpha :S\rightarrow \mathbb {Z}_\ell $
are understood, we simply denote it by
![]() $\mu $
. On the other hand, the
$\mu $
. On the other hand, the
![]() $\lambda $
-invariant is defined to be the quantity
$\lambda $
-invariant is defined to be the quantity
Remark 2.12.
-
• According to Lemma 2.10, we have that
 $f(T)\neq 0$
, and thus the
$f(T)\neq 0$
, and thus the
 $\mu $
and
$\mu $
and
 $\lambda $
invariants are defined.
$\lambda $
invariants are defined. -
• The
 $\nu $
-invariant is not detectable from the characteristic series, and we postpone its definition till Definition 2.14.
$\nu $
-invariant is not detectable from the characteristic series, and we postpone its definition till Definition 2.14. -
• In our setting the
 $\lambda $
-invariant is not the degree of
$\lambda $
-invariant is not the degree of
 $g(T)$
, that is, the conventional definition of the
$g(T)$
, that is, the conventional definition of the
 $\lambda $
-invariant of a power series
$\lambda $
-invariant of a power series
 $f(T)$
. The shift by
$f(T)$
. The shift by
 $-1$
is necessary in studying the growth of Picard numbers in a
$-1$
is necessary in studying the growth of Picard numbers in a
 $\mathbb {Z}_\ell $
-tower.
$\mathbb {Z}_\ell $
-tower.
Let
![]() $\alpha :S\rightarrow \mathbb {Z}_\ell $
be a function such that Assumption 2.6 is satisfied. Given
$\alpha :S\rightarrow \mathbb {Z}_\ell $
be a function such that Assumption 2.6 is satisfied. Given
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $X_n=X(\mathbb {Z}/\ell ^n\mathbb {Z}, S, \alpha _{/n})$
and write
$X_n=X(\mathbb {Z}/\ell ^n\mathbb {Z}, S, \alpha _{/n})$
and write
![]() $\kappa _n$
for the number of spanning trees of
$\kappa _n$
for the number of spanning trees of
![]() $X_n$
. Let
$X_n$
. Let
![]() $|\cdot |_\ell :\mathbb {Q}_\ell \rightarrow \mathbb {R}_{\geq 0}$
be the absolute value normalized by setting
$|\cdot |_\ell :\mathbb {Q}_\ell \rightarrow \mathbb {R}_{\geq 0}$
be the absolute value normalized by setting
![]() $|\ell |_\ell ^{-1}=\ell $
. The
$|\ell |_\ell ^{-1}=\ell $
. The
![]() $\ell $
-part of
$\ell $
-part of
![]() $\kappa _n$
is defined as
$\kappa _n$
is defined as
![]() $\kappa _\ell (X_n):=|\kappa _n|_\ell ^{-1}$
. The following result is [Reference McGown and Vallières20, Th. 6.1].
$\kappa _\ell (X_n):=|\kappa _n|_\ell ^{-1}$
. The following result is [Reference McGown and Vallières20, Th. 6.1].
Theorem 2.13 (McGown–Vallières).
Let
![]() $\ell $
be a prime and
$\ell $
be a prime and
![]() $\alpha $
be as above. Then, there exist
$\alpha $
be as above. Then, there exist
![]() $n_0>0$
and
$n_0>0$
and
![]() $\nu \in \mathbb {Z}$
, such that
$\nu \in \mathbb {Z}$
, such that
for all
![]() $n\geq n_0$
. The invariants
$n\geq n_0$
. The invariants
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
are given as in Definition 2.11.
$\lambda $
are given as in Definition 2.11.
Definition 2.14. The
![]() $\nu $
-invariant is the uniquely determined constant for which the asymptotic formula (2.4) holds.
$\nu $
-invariant is the uniquely determined constant for which the asymptotic formula (2.4) holds.
2.3 Connectedness of multigraphs in abelian
 $\ell $
-towers
$\ell $
-towers
Let X be a connected multigraph, let
![]() $\ell $
be a prime number, and let
$\ell $
be a prime number, and let
![]() $\alpha :S\rightarrow \mathbb {Z}_\ell $
. In this section, we introduce explicit conditions on X which are sufficient for Assumption 2.6 to hold. Let
$\alpha :S\rightarrow \mathbb {Z}_\ell $
. In this section, we introduce explicit conditions on X which are sufficient for Assumption 2.6 to hold. Let
be an abelian
![]() $\ell $
-tower over X. Set also
$\ell $
-tower over X. Set also
![]() $G_{n} = \mathrm {Gal}(X_{n}/X)$
. We have natural group morphisms
$G_{n} = \mathrm {Gal}(X_{n}/X)$
. We have natural group morphisms
that are compatible so that we get a group morphism
Fix now a spanning tree of X, say
![]() $\mathfrak {T}\subseteq E_X$
, a section
$\mathfrak {T}\subseteq E_X$
, a section
![]() $\gamma :E_{X} \to E_{X}^+$
, and set
$\gamma :E_{X} \to E_{X}^+$
, and set
![]() $S:=\gamma (E_{X})$
. We let
$S:=\gamma (E_{X})$
. We let
![]() $S(\mathfrak {T})$
be the collection of
$S(\mathfrak {T})$
be the collection of
![]() $s \in S$
such that
$s \in S$
such that
![]() $\pi (s) \in \mathfrak {T}$
. For each
$\pi (s) \in \mathfrak {T}$
. For each
![]() $s \in S$
, let
$s \in S$
, let
![]() $c_{s} = d_{s} \cdot s$
be the closed path in X, where
$c_{s} = d_{s} \cdot s$
be the closed path in X, where
![]() $d_{s}$
is the unique geodesic path in
$d_{s}$
is the unique geodesic path in
![]() $\mathfrak {T}$
going from
$\mathfrak {T}$
going from
![]() $t(s)$
to
$t(s)$
to
![]() $o(s)$
. Let
$o(s)$
. Let
![]() $\langle c_{s} \rangle $
be the corresponding cycle in
$\langle c_{s} \rangle $
be the corresponding cycle in
![]() $H_{1}(X,\mathbb {Z})$
. Note that if
$H_{1}(X,\mathbb {Z})$
. Note that if
![]() $s \in S(\mathfrak {T})$
, then
$s \in S(\mathfrak {T})$
, then
![]() $\langle c_{s} \rangle = 0$
. The collection
$\langle c_{s} \rangle = 0$
. The collection
forms a basis of
![]() $H_{1}(X,\mathbb {Z})$
(cf. [Reference Sunada24, Sec. 4.3]), so that, in particular,
$H_{1}(X,\mathbb {Z})$
(cf. [Reference Sunada24, Sec. 4.3]), so that, in particular,
Define now
![]() $\alpha :S \to \mathbb {Z}_{\ell }$
via
$\alpha :S \to \mathbb {Z}_{\ell }$
via
![]() $s \mapsto \alpha (s) = \gamma (\langle c_{s} \rangle )$
. By successively lifting, the tree
$s \mapsto \alpha (s) = \gamma (\langle c_{s} \rangle )$
. By successively lifting, the tree
![]() $\mathfrak {T}$
to
$\mathfrak {T}$
to
![]() $X_{1}$
, then to
$X_{1}$
, then to
![]() $X_{2}$
and so on, one can construct isomorphisms of multigraphs
$X_{2}$
and so on, one can construct isomorphisms of multigraphs
for which all the squares and the triangle in the diagram

commute. In other words, once a spanning tree
![]() $\mathfrak {T}$
for X has been fixed (which also specifies a
$\mathfrak {T}$
for X has been fixed (which also specifies a
![]() $\mathbb {Z}$
-basis for
$\mathbb {Z}$
-basis for
![]() $H_{1}(X,\mathbb {Z})$
), every abelian
$H_{1}(X,\mathbb {Z})$
), every abelian
![]() $\ell $
-tower over X arises from a function
$\ell $
-tower over X arises from a function
![]() $\alpha :S \to \mathbb {Z}_{\ell }$
satisfying
$\alpha :S \to \mathbb {Z}_{\ell }$
satisfying
![]() $\alpha (s) = 0$
for all
$\alpha (s) = 0$
for all
![]() $s \in S(\mathfrak {T})$
.
$s \in S(\mathfrak {T})$
.
Theorem 2.15. Let X be a connected multigraph, and let
![]() $\mathfrak {T}\subseteq E_X$
be a fixed spanning tree of X. Furthermore, let S be the image of a section as above, and let
$\mathfrak {T}\subseteq E_X$
be a fixed spanning tree of X. Furthermore, let S be the image of a section as above, and let
![]() $\alpha :S \to \mathbb {Z}_{\ell }$
be a function satisfying
$\alpha :S \to \mathbb {Z}_{\ell }$
be a function satisfying
![]() $\alpha (s) = 0$
for all
$\alpha (s) = 0$
for all
![]() $s \in S(\mathfrak {T})$
. Then
$s \in S(\mathfrak {T})$
. Then
![]() $X(\mathbb {Z}/\ell ^{n}\mathbb {Z},S,\alpha _{/n})$
is connected for all positive integer n if and only if there exists
$X(\mathbb {Z}/\ell ^{n}\mathbb {Z},S,\alpha _{/n})$
is connected for all positive integer n if and only if there exists
![]() $s \in S \smallsetminus S(\mathfrak {T})$
such that
$s \in S \smallsetminus S(\mathfrak {T})$
such that
![]() $\alpha (s)\in \mathbb {Z}_\ell ^\times $
.
$\alpha (s)\in \mathbb {Z}_\ell ^\times $
.
Proof. Let us assume first that there exists
![]() $s \in S \smallsetminus S(\mathfrak {T})$
such that
$s \in S \smallsetminus S(\mathfrak {T})$
such that
![]() $(\alpha (s),\ell )=1$
. Let also
$(\alpha (s),\ell )=1$
. Let also
![]() $X_{n} = X(\mathbb {Z}/\ell ^{n}\mathbb {Z},S,\alpha _{/n})$
. Let
$X_{n} = X(\mathbb {Z}/\ell ^{n}\mathbb {Z},S,\alpha _{/n})$
. Let
![]() $v\in V_X$
,
$v\in V_X$
,
![]() $e\in E_X^+$
and
$e\in E_X^+$
and
![]() $\bar {a}\in \mathbb {Z}/\ell ^n\mathbb {Z}$
. The map
$\bar {a}\in \mathbb {Z}/\ell ^n\mathbb {Z}$
. The map
![]() $p_{n}:X_{n} \to X$
defined via
$p_{n}:X_{n} \to X$
defined via
is a morphism of multigraphs (recall that the vertices and (directed) edges of
![]() $X_n$
consist of elements in
$X_n$
consist of elements in
![]() $V_X\times \mathbb {Z}/\ell ^n\mathbb {Z}$
and
$V_X\times \mathbb {Z}/\ell ^n\mathbb {Z}$
and
![]() $E_X^+\times \mathbb {Z}/\ell ^n\mathbb {Z}$
, respectively). Furthermore, for all
$E_X^+\times \mathbb {Z}/\ell ^n\mathbb {Z}$
, respectively). Furthermore, for all
![]() $w \in V_{X_{n}}$
, the restriction
$w \in V_{X_{n}}$
, the restriction
![]() $p_{n}|_{E_{X_{n},w}}$
induces a bijection
$p_{n}|_{E_{X_{n},w}}$
induces a bijection
It follows that every path c in X has a unique lift
![]() $\tilde {c}$
to
$\tilde {c}$
to
![]() $X_{n}$
once the starting point in the fiber of
$X_{n}$
once the starting point in the fiber of
![]() $o(c)$
is fixed. Furthermore, since
$o(c)$
is fixed. Furthermore, since
![]() $p_{n}$
is a morphism of multigraphs one has
$p_{n}$
is a morphism of multigraphs one has
Now,
![]() $\mathbb {Z}/\ell ^{n}\mathbb {Z}$
acts on
$\mathbb {Z}/\ell ^{n}\mathbb {Z}$
acts on
![]() $X_{n}$
via
$X_{n}$
via
which gives an injective group morphism
Let
![]() $v_{1},v_{2} \in V_{X}$
be arbitrary. Since X is connected, there is a path c in X satisfying
$v_{1},v_{2} \in V_{X}$
be arbitrary. Since X is connected, there is a path c in X satisfying
![]() $o(c)=v_{1}$
and
$o(c)=v_{1}$
and
![]() $t(c) = v_{2}$
. Thus, by lifting c and using (2.5), for any vertex
$t(c) = v_{2}$
. Thus, by lifting c and using (2.5), for any vertex
![]() $w \in p_{n}^{-1}(v_{1})$
, there exists a path
$w \in p_{n}^{-1}(v_{1})$
, there exists a path
![]() $\tilde {c}$
in
$\tilde {c}$
in
![]() $X_{n}$
going from w to another vertex in
$X_{n}$
going from w to another vertex in
![]() $p_{n}^{-1}(v_{2})$
. It follows that in order to show that
$p_{n}^{-1}(v_{2})$
. It follows that in order to show that
![]() $X_{n}$
is connected, it suffices to show that every vertex in a single fiber can be joined via a path in
$X_{n}$
is connected, it suffices to show that every vertex in a single fiber can be joined via a path in
![]() $X_{n}$
. Under our assumption, there exists
$X_{n}$
. Under our assumption, there exists
![]() $s_{0} \in S \smallsetminus S(\mathfrak {T})$
such that
$s_{0} \in S \smallsetminus S(\mathfrak {T})$
such that
![]() $(\alpha (s_{0}),\ell )=1$
, and thus,
$(\alpha (s_{0}),\ell )=1$
, and thus,
![]() $\alpha _{/n}(s_{0})$
is a generator for
$\alpha _{/n}(s_{0})$
is a generator for
![]() $\mathbb {Z}/\ell ^{n}\mathbb {Z}$
. Let
$\mathbb {Z}/\ell ^{n}\mathbb {Z}$
. Let
![]() $v \in V_{X}$
be such that
$v \in V_{X}$
be such that
![]() $v = t(s_{0}),$
and let
$v = t(s_{0}),$
and let
![]() $\sigma _{0} = \alpha _{/n}(s_{0}) \in \mathbb {Z}/\ell ^{n}\mathbb {Z}$
. The closed path
$\sigma _{0} = \alpha _{/n}(s_{0}) \in \mathbb {Z}/\ell ^{n}\mathbb {Z}$
. The closed path
![]() $c_{s_{0}} = d_{s_{0}}\cdot s_{0}$
can be lifted to a path
$c_{s_{0}} = d_{s_{0}}\cdot s_{0}$
can be lifted to a path
![]() $\tilde {c}_{s_{0}}$
in
$\tilde {c}_{s_{0}}$
in
![]() $X_{n}$
starting at
$X_{n}$
starting at
![]() $(v,\bar {0})$
. Furthermore, since
$(v,\bar {0})$
. Furthermore, since
![]() $\alpha (s) = 0$
for all
$\alpha (s) = 0$
for all
![]() $s \in S(\mathfrak {T})$
, we have
$s \in S(\mathfrak {T})$
, we have
![]() $t(\tilde {c}_{s_{0}}) = (v,\sigma _{0})$
. The path
$t(\tilde {c}_{s_{0}}) = (v,\sigma _{0})$
. The path
![]() $\tilde {c}_{s_{0}} \cdot \sigma _{0}(\tilde {c}_{s_{0}})$
will start at
$\tilde {c}_{s_{0}} \cdot \sigma _{0}(\tilde {c}_{s_{0}})$
will start at
![]() $(v,\bar {0})$
and end at
$(v,\bar {0})$
and end at
![]() $(v,2\cdot \sigma _{0})$
. Keeping going like this, we can find a path in
$(v,2\cdot \sigma _{0})$
. Keeping going like this, we can find a path in
![]() $X_{n}$
going from
$X_{n}$
going from
![]() $(v,\bar {0})$
to
$(v,\bar {0})$
to
![]() $(v,m\cdot \sigma _{0})$
for all positive integer m. Since
$(v,m\cdot \sigma _{0})$
for all positive integer m. Since
![]() $\sigma _{0}$
generates
$\sigma _{0}$
generates
![]() $\mathbb {Z}/\ell ^{n}\mathbb {Z}$
, this shows that every vertex in the fiber of v can be joined via a path in
$\mathbb {Z}/\ell ^{n}\mathbb {Z}$
, this shows that every vertex in the fiber of v can be joined via a path in
![]() $X_{n}$
. It follows that
$X_{n}$
. It follows that
![]() $X_{n}$
is connected.
$X_{n}$
is connected.
Conversely, assume that all multigraphs
![]() $X_{n}$
are connected. In particular,
$X_{n}$
are connected. In particular,
![]() $X_{1}$
is connected. To simplify the notation, write
$X_{1}$
is connected. To simplify the notation, write
![]() $S \smallsetminus S(\mathfrak {T}) = \{s_{1},\ldots ,s_{t} \}$
. The function
$S \smallsetminus S(\mathfrak {T}) = \{s_{1},\ldots ,s_{t} \}$
. The function
![]() $\alpha $
induces a function on
$\alpha $
induces a function on
![]() $C_{1}(X,\mathbb {Z})$
and thus also on
$C_{1}(X,\mathbb {Z})$
and thus also on
![]() $H_{1}(X,\mathbb {Z})$
by restriction. Let also
$H_{1}(X,\mathbb {Z})$
by restriction. Let also
![]() $v \in V_{X}$
be a fixed vertex. Since we are assuming that
$v \in V_{X}$
be a fixed vertex. Since we are assuming that
![]() $X_{1}$
is connected, there exists a path
$X_{1}$
is connected, there exists a path
![]() $\tilde {c}$
in
$\tilde {c}$
in
![]() $X_{1}$
going from
$X_{1}$
going from
![]() $(v,\bar {0})$
to
$(v,\bar {0})$
to
![]() $(v,\bar {1})$
. The path
$(v,\bar {1})$
. The path
![]() $c = p_{1}(\tilde {c})$
is then a closed path in X, and
$c = p_{1}(\tilde {c})$
is then a closed path in X, and
![]() $\alpha (\langle c \rangle ) = \bar {1}$
. Since the
$\alpha (\langle c \rangle ) = \bar {1}$
. Since the
![]() $\langle c_{s_{i}} \rangle $
for
$\langle c_{s_{i}} \rangle $
for
![]() $i=1,\ldots ,t$
form a
$i=1,\ldots ,t$
form a
![]() $\mathbb {Z}$
-basis of
$\mathbb {Z}$
-basis of
![]() $H_{1}(X,\mathbb {Z})$
, we have
$H_{1}(X,\mathbb {Z})$
, we have
for some
![]() $n_{i} \in \mathbb {Z}$
. Applying
$n_{i} \in \mathbb {Z}$
. Applying
![]() $\alpha _{/1}$
to this last equation gives
$\alpha _{/1}$
to this last equation gives
Now, if all the
![]() $\alpha (s_{i})$
were divisible by
$\alpha (s_{i})$
were divisible by
![]() $\ell $
, then we would get a contradiction.
$\ell $
, then we would get a contradiction.
The following corollary is most likely well known, we list it here for convenience.
Corollary 2.16. Let X be a bouquet and
![]() $\alpha :S\rightarrow \mathbb {Z}_\ell $
. Then, Assumption 2.6 is satisfied if and only if there exists
$\alpha :S\rightarrow \mathbb {Z}_\ell $
. Then, Assumption 2.6 is satisfied if and only if there exists
![]() $s\in S$
for which
$s\in S$
for which
![]() $\ell \nmid \alpha (s)$
.
$\ell \nmid \alpha (s)$
.
Proof. Since X is a bouquet, the only possible spanning tree consists of the single vertex of X (and no edges). The result follows from Theorem 2.15.
2.4 Basic properties of Iwasawa invariants
In this section, we prove a number of basic results about the Iwasawa
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
invariants associated with multigraphs. The graph X is called a bouquet if there is one vertex, in which case
$\lambda $
invariants associated with multigraphs. The graph X is called a bouquet if there is one vertex, in which case
![]() $M(x)$
is a
$M(x)$
is a
![]() $1\times 1$
-matrix. Suppose that there are t loops in total, labeled
$1\times 1$
-matrix. Suppose that there are t loops in total, labeled
![]() $e_1,\dots , e_t$
and
$e_1,\dots , e_t$
and
![]() $\alpha =(\alpha _1,\dots , \alpha _t)$
sends
$\alpha =(\alpha _1,\dots , \alpha _t)$
sends
![]() $e_i\mapsto \alpha _i$
. We denote the corresponding bouquet by
$e_i\mapsto \alpha _i$
. We denote the corresponding bouquet by
![]() $X_t$
. We shall set
$X_t$
. We shall set
![]() $\mu :=\mu _\ell (X_t;\alpha )$
and
$\mu :=\mu _\ell (X_t;\alpha )$
and
![]() $\lambda :=\lambda _\ell (X_t;\alpha )$
. Given
$\lambda :=\lambda _\ell (X_t;\alpha )$
. Given
![]() $a\in \mathbb {Z}_\ell $
, let
$a\in \mathbb {Z}_\ell $
, let
 $$\begin{align*}f_a(T)=2-(1+T)^a-(1+T)^{-a}=-\sum_{i\geq 2}\left({a\choose i}+{-a\choose i}\right) T^i.\end{align*}$$
$$\begin{align*}f_a(T)=2-(1+T)^a-(1+T)^{-a}=-\sum_{i\geq 2}\left({a\choose i}+{-a\choose i}\right) T^i.\end{align*}$$
We have that
![]() $f(T)=\sum _{j=1}^t f_{\alpha _j}(T)$
, and therefore, we may write
$f(T)=\sum _{j=1}^t f_{\alpha _j}(T)$
, and therefore, we may write
 $$\begin{align*}f(T)=\sum_{n\geq 2} \beta_{n} T^n\end{align*}$$
$$\begin{align*}f(T)=\sum_{n\geq 2} \beta_{n} T^n\end{align*}$$
with
![]() $\beta _2=-\left (\sum _{j} \alpha _j^2\right )$
. In particular, we find that
$\beta _2=-\left (\sum _{j} \alpha _j^2\right )$
. In particular, we find that
![]() $\operatorname {ord}_{T=0} f(T)\geq 2$
, and thus
$\operatorname {ord}_{T=0} f(T)\geq 2$
, and thus
![]() $\lambda \geq 1$
. It is easy to see that
$\lambda \geq 1$
. It is easy to see that
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =1$
if and only if
$\lambda =1$
if and only if
![]() $\beta _2$
is a unit in
$\beta _2$
is a unit in
![]() $\mathbb {Z}_\ell $
. These are the minimal values of the Iwasawa invariants attainable by a bouquet. The following result shows that the Iwasawa invariants
$\mathbb {Z}_\ell $
. These are the minimal values of the Iwasawa invariants attainable by a bouquet. The following result shows that the Iwasawa invariants
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
can be arbitrarily large.
$\lambda $
can be arbitrarily large.
Lemma 2.17. Let
![]() $n_1\in \mathbb {Z}_{\geq 0}$
,
$n_1\in \mathbb {Z}_{\geq 0}$
,
![]() $n_2\in \mathbb {Z}_{\geq 1}$
, and let
$n_2\in \mathbb {Z}_{\geq 1}$
, and let
![]() $\ell $
be a prime number. There is a bouquet
$\ell $
be a prime number. There is a bouquet
![]() $X_t$
consisting of
$X_t$
consisting of
![]() $t = \ell ^{n_{1}+1} + \ell ^{n_{1}}$
loops and a choice of vector
$t = \ell ^{n_{1}+1} + \ell ^{n_{1}}$
loops and a choice of vector
![]() $\alpha \in \left (\mathbb {Z}_{\ell }^t\backslash (\ell \mathbb {Z}_{\ell })^t\right )$
(which depends on both
$\alpha \in \left (\mathbb {Z}_{\ell }^t\backslash (\ell \mathbb {Z}_{\ell })^t\right )$
(which depends on both
![]() $n_1$
and
$n_1$
and
![]() $n_2$
) such that the associated Iwasawa invariants satisfy
$n_2$
) such that the associated Iwasawa invariants satisfy
Proof. Set
![]() $t=\ell ^{n_1+1}+\ell ^{n_1}$
and let
$t=\ell ^{n_1+1}+\ell ^{n_1}$
and let
![]() $\alpha =(\alpha _1, \dots , \alpha _t)$
with
$\alpha =(\alpha _1, \dots , \alpha _t)$
with
 $$\begin{align*}\alpha_i=\begin{cases} 1,&\text{ if }i\leq \ell^{n_1+1},\\ \ell^{n_2}, &\text{ if }i> \ell^{n_1+1}.\\ \end{cases}\end{align*}$$
$$\begin{align*}\alpha_i=\begin{cases} 1,&\text{ if }i\leq \ell^{n_1+1},\\ \ell^{n_2}, &\text{ if }i> \ell^{n_1+1}.\\ \end{cases}\end{align*}$$
We have that
and that
As a result, we find that
 $$ \begin{align*}f(T)=&\ \ell^{n_1}\left(\ell f_1(T)+f_{\ell ^{n_2}}(T)\right),\\ = & -\ell^{n_1} (1+T)^{-\ell ^{n_2}}\left(\ell (1+T)^{\ell ^{n_2-1}}T^2 +\left(1-(1+T)^{\ell ^{n_2}}\right)^2\right).\end{align*} $$
$$ \begin{align*}f(T)=&\ \ell^{n_1}\left(\ell f_1(T)+f_{\ell ^{n_2}}(T)\right),\\ = & -\ell^{n_1} (1+T)^{-\ell ^{n_2}}\left(\ell (1+T)^{\ell ^{n_2-1}}T^2 +\left(1-(1+T)^{\ell ^{n_2}}\right)^2\right).\end{align*} $$
The degree of
![]() $\left (1-(1+T)^{\ell ^{n_2}}\right )^2$
is
$\left (1-(1+T)^{\ell ^{n_2}}\right )^2$
is
![]() $2 \ell ^{n_2}$
, which is larger than the degree of
$2 \ell ^{n_2}$
, which is larger than the degree of
![]() $(1+T)^{\ell ^{n_2-1}}T^2$
. Furthermore, all non-leading coefficients of
$(1+T)^{\ell ^{n_2-1}}T^2$
. Furthermore, all non-leading coefficients of
![]() $\left (1-(1+T)^{\ell ^{n_2}}\right )^2$
are divisible by
$\left (1-(1+T)^{\ell ^{n_2}}\right )^2$
are divisible by
![]() $\ell $
. We have shown that
$\ell $
. We have shown that
![]() $P(T):=\ell (1+T)^{\ell ^{n_2-1}}T^2 +\left (1-(1+T)^{\ell ^{n_2}}\right )^2$
is a distinguished polynomial. Thus,
$P(T):=\ell (1+T)^{\ell ^{n_2-1}}T^2 +\left (1-(1+T)^{\ell ^{n_2}}\right )^2$
is a distinguished polynomial. Thus,
![]() $f(T)=\ell ^{n_1}u(T)P(T)$
, where
$f(T)=\ell ^{n_1}u(T)P(T)$
, where
![]() $u(T)=-(1+T)^{-\ell ^{n_2}}$
is a unit in the Iwasawa algebra and
$u(T)=-(1+T)^{-\ell ^{n_2}}$
is a unit in the Iwasawa algebra and
![]() $P(T)$
is a distinguished polynomial of degree
$P(T)$
is a distinguished polynomial of degree
![]() $2\ell ^{n_2}$
. Thus, we have shown that
$2\ell ^{n_2}$
. Thus, we have shown that
![]() $\mu =n_1$
and
$\mu =n_1$
and
![]() $\lambda =2\ell ^{n_2}-1$
.
$\lambda =2\ell ^{n_2}-1$
.
Theorem 2.18. Let X be a multigraph, let
![]() $\ell $
be an odd prime, and let
$\ell $
be an odd prime, and let
![]() $\alpha :S\rightarrow \mathbb {Z}_\ell $
be a function such that Assumption 2.6 is satisfied. Then,
$\alpha :S\rightarrow \mathbb {Z}_\ell $
be a function such that Assumption 2.6 is satisfied. Then,
![]() $\lambda _\ell (X, \alpha )$
is odd.
$\lambda _\ell (X, \alpha )$
is odd.
Proof. Set
![]() $\dot {T}:=(1+T)^{-1}-1$
and note that
$\dot {T}:=(1+T)^{-1}-1$
and note that
for all
![]() $a\in \mathbb {Z}_\ell $
. Note that
$a\in \mathbb {Z}_\ell $
. Note that
![]() $M(x)^t=M(x^{-1})$
and it follows from (2.6) that
$M(x)^t=M(x^{-1})$
and it follows from (2.6) that
Write
![]() $f(T)=\ell ^\mu P(T) u(T)$
, where
$f(T)=\ell ^\mu P(T) u(T)$
, where
![]() $P(T)=\sum _{j=0}^{\lambda } \xi _j T^j+ T^{\lambda +1}$
and
$P(T)=\sum _{j=0}^{\lambda } \xi _j T^j+ T^{\lambda +1}$
and
![]() $\xi _j$
are all divisible by
$\xi _j$
are all divisible by
![]() $\ell $
. Note that
$\ell $
. Note that
 $$\begin{align*}(1+T)^{\lambda+1} P(\dot{T})=\sum_{j=0}^{\lambda} (-1)^{j}\xi_j (1+T)^{\lambda+1-j}T^j+ (-1)^{\lambda+1} T^{\lambda+1}.\end{align*}$$
$$\begin{align*}(1+T)^{\lambda+1} P(\dot{T})=\sum_{j=0}^{\lambda} (-1)^{j}\xi_j (1+T)^{\lambda+1-j}T^j+ (-1)^{\lambda+1} T^{\lambda+1}.\end{align*}$$
We see that
![]() $P(-1)=\sum _{j=0}^{\lambda } \xi _j (-1)^j+(-1)^{\lambda +1}\equiv (-1)^{\lambda +1} \bmod {\ell }$
, and hence,
$P(-1)=\sum _{j=0}^{\lambda } \xi _j (-1)^j+(-1)^{\lambda +1}\equiv (-1)^{\lambda +1} \bmod {\ell }$
, and hence,
![]() $P(-1)$
is a unit in
$P(-1)$
is a unit in
![]() $\mathbb {Z}_\ell $
. The above relation shows that
$\mathbb {Z}_\ell $
. The above relation shows that
![]() $P(-1)^{-1}(1+T)^{\lambda +1}P(\dot {T})$
is the distinguished polynomial dividing
$P(-1)^{-1}(1+T)^{\lambda +1}P(\dot {T})$
is the distinguished polynomial dividing
![]() $f(\dot {T})=f(T)$
, thus
$f(\dot {T})=f(T)$
, thus
and
The latter relation specialized to
![]() $T=0$
gives
$T=0$
gives
![]() $P(-1)=1$
. Thus, we have shown that
$P(-1)=1$
. Thus, we have shown that
![]() $1\equiv (-1)^{\lambda +1} \bmod {\ell }$
, and since
$1\equiv (-1)^{\lambda +1} \bmod {\ell }$
, and since
![]() $\ell $
is assumed to be odd, it follows that
$\ell $
is assumed to be odd, it follows that
![]() $\lambda $
is odd.
$\lambda $
is odd.
3 Equations over finite fields
Let
![]() $\ell $
be a prime (
$\ell $
be a prime (
![]() $\ell =2$
is allowed), and let q be a power of
$\ell =2$
is allowed), and let q be a power of
![]() $\ell $
. Denote by
$\ell $
. Denote by
![]() $\mathbb {F}_q$
the finite field with q elements, and let
$\mathbb {F}_q$
the finite field with q elements, and let
![]() $f_1, \dots , f_m\in \mathbb {F}_q[x_1, \dots , x_n]$
. In this section, we catalog some well-known results on the number of solutions to the system of equations
$f_1, \dots , f_m\in \mathbb {F}_q[x_1, \dots , x_n]$
. In this section, we catalog some well-known results on the number of solutions to the system of equations
![]() $f_1=f_2=\dots =f_m=0$
.
$f_1=f_2=\dots =f_m=0$
.
3.1 Systems of equations
We begin with a generalization of the Chevalley–Warning theorem to a system of equations in many variables. Associate to
![]() $I=(i_1, \dots , i_n)\in \mathbb {Z}_{\geq 0}^n$
, the monomial
$I=(i_1, \dots , i_n)\in \mathbb {Z}_{\geq 0}^n$
, the monomial
![]() $x_I:=x_1^{i_1}x_2^{i_2}\dots x_n^{i_n}$
, then define the degree to be the sum
$x_I:=x_1^{i_1}x_2^{i_2}\dots x_n^{i_n}$
, then define the degree to be the sum
Given
![]() $f(x_1, \dots , x_n)=\sum _I c_I x_I$
, the degree of f is defined as follows:
$f(x_1, \dots , x_n)=\sum _I c_I x_I$
, the degree of f is defined as follows:
The polynomial is homogenous of degree d if
![]() $\operatorname {deg}(x_I)=d$
for all I such that
$\operatorname {deg}(x_I)=d$
for all I such that
![]() $c_I\neq 0$
. The following is often referred to as Warning’s second theorem, compare [Reference Warning27].
$c_I\neq 0$
. The following is often referred to as Warning’s second theorem, compare [Reference Warning27].
Theorem 3.1. Let
![]() $m, n\in \mathbb {Z}_{\geq 1}$
and
$m, n\in \mathbb {Z}_{\geq 1}$
and
![]() $f_1,\dots , f_m\in \mathbb {F}_q[x_1, \dots , x_n]$
. Assume that
$f_1,\dots , f_m\in \mathbb {F}_q[x_1, \dots , x_n]$
. Assume that
 $$\begin{align*}d:=\sum_{i=1}^m \operatorname{deg}(f_i)<n,\end{align*}$$
$$\begin{align*}d:=\sum_{i=1}^m \operatorname{deg}(f_i)<n,\end{align*}$$
and that for all i, we have that
![]() $f_i(0,0,\dots , 0)=0$
. Let N be the number of solutions of
$f_i(0,0,\dots , 0)=0$
. Let N be the number of solutions of
![]() $f_1=f_2=\dots =f_m=0$
. Then, N is divisible by
$f_1=f_2=\dots =f_m=0$
. Then, N is divisible by
![]() $\ell $
and
$\ell $
and
![]() $N\geq q^{n-d}$
.
$N\geq q^{n-d}$
.
Proof. The result follows from [Reference Lidl and Niederreiter17, Th. 6.11].
3.2 Quadratic forms and their solutions
A quadratic form is a homogenous polynomial of degree
![]() $2$
. Assume throughout that q is odd, let
$2$
. Assume throughout that q is odd, let
![]() $\eta :\mathbb {F}_q^\times \rightarrow \{\pm 1\}$
be the quadratic character of
$\eta :\mathbb {F}_q^\times \rightarrow \{\pm 1\}$
be the quadratic character of
![]() $\mathbb {F}_q$
, and extend
$\mathbb {F}_q$
, and extend
![]() $\eta $
to a function on
$\eta $
to a function on
![]() $\mathbb {F}_q$
by setting
$\mathbb {F}_q$
by setting
![]() $\eta (0)=0$
. Given a quadratic form
$\eta (0)=0$
. Given a quadratic form
![]() $Q(x_1,\dots , x_n)$
over
$Q(x_1,\dots , x_n)$
over
![]() $\mathbb {F}_q$
, express Q as
$\mathbb {F}_q$
, express Q as
 $$\begin{align*}Q(x_1,\dots, x_n)=\sum_{i,j} a_{i,j} x_i x_j,\end{align*}$$
$$\begin{align*}Q(x_1,\dots, x_n)=\sum_{i,j} a_{i,j} x_i x_j,\end{align*}$$
with
![]() $a_{i,j}=a_{j,i}$
. The rank of Q is the rank of the associated matrix
$a_{i,j}=a_{j,i}$
. The rank of Q is the rank of the associated matrix
![]() $A=(a_{i,j})$
over
$A=(a_{i,j})$
over
![]() $\mathbb {F}_q$
. We let
$\mathbb {F}_q$
. We let
![]() $\operatorname {det} Q$
denote the determinant of A. The form Q is nondegenerate if
$\operatorname {det} Q$
denote the determinant of A. The form Q is nondegenerate if
![]() $\operatorname {rank}A=n$
, that is, A is non-singular. On the other hand, Q is diagonal if
$\operatorname {rank}A=n$
, that is, A is non-singular. On the other hand, Q is diagonal if
![]() $a_{i,j}=0$
unless
$a_{i,j}=0$
unless
![]() $i=j$
.
$i=j$
.
Proposition 3.2. Suppose that
![]() $\ell $
is odd and q is a power of
$\ell $
is odd and q is a power of
![]() $\ell $
. Then, any quadratic form over
$\ell $
. Then, any quadratic form over
![]() $\mathbb {F}_q$
is equivalent to a diagonal form.
$\mathbb {F}_q$
is equivalent to a diagonal form.
Proof. The above result is [Reference Lidl and Niederreiter17, Th. 6.21].
Let
![]() $v:\mathbb {F}_q\rightarrow \mathbb {Z}$
be the function defined by
$v:\mathbb {F}_q\rightarrow \mathbb {Z}$
be the function defined by
 $$\begin{align*}v(b):=\begin{cases} -1, &\text{ if }b\neq 0, \\ (q-1),&\text{ if }b=0. \end{cases}\end{align*}$$
$$\begin{align*}v(b):=\begin{cases} -1, &\text{ if }b\neq 0, \\ (q-1),&\text{ if }b=0. \end{cases}\end{align*}$$
Theorem 3.3. Let
![]() $Q(x_1, \dots , x_n)$
be a nonzero quadratic form over
$Q(x_1, \dots , x_n)$
be a nonzero quadratic form over
![]() $\mathbb {F}_q$
, and assume that q is odd and n is even. For
$\mathbb {F}_q$
, and assume that q is odd and n is even. For
![]() $b\in \mathbb {F}_q$
, let
$b\in \mathbb {F}_q$
, let
![]() $N\left (Q(x_1,\dots , x_n)=b\right )$
be the number of solutions to
$N\left (Q(x_1,\dots , x_n)=b\right )$
be the number of solutions to
![]() $Q(x_1,\dots , x_n)=b$
. Then, we have that
$Q(x_1,\dots , x_n)=b$
. Then, we have that
where
![]() $\eta $
is the quadratic character of
$\eta $
is the quadratic character of
![]() $\mathbb {F}_q$
and
$\mathbb {F}_q$
and
![]() $\Delta =\operatorname {det} Q$
.
$\Delta =\operatorname {det} Q$
.
Proof. The result above is [Reference Lidl and Niederreiter17, Th. 6.26].
Given a degenerate quadratic form
![]() $Q(x_1, \dots , x_n)$
, we let
$Q(x_1, \dots , x_n)$
, we let
![]() $\mathfrak {r}$
denote the rank of Q. According to Proposition 3.2, Q is equivalent to the form
$\mathfrak {r}$
denote the rank of Q. According to Proposition 3.2, Q is equivalent to the form
![]() $\sum _{i=1}^{\mathfrak {r}} a_i x_i^2$
, where
$\sum _{i=1}^{\mathfrak {r}} a_i x_i^2$
, where
![]() $a_i$
are all nonzero. We set
$a_i$
are all nonzero. We set
![]() $Q_0(x_1,\dots , x_{\mathfrak {r}})\in \mathbb {F}_q[x_1, \dots , x_{\mathfrak {r}}]$
to be the nondegenerate form
$Q_0(x_1,\dots , x_{\mathfrak {r}})\in \mathbb {F}_q[x_1, \dots , x_{\mathfrak {r}}]$
to be the nondegenerate form
![]() $Q_0(x_1, \dots , x_{\mathfrak {r}})=\sum _{i=1}^{\mathfrak {r}} a_i x_i^2$
, with discriminant
$Q_0(x_1, \dots , x_{\mathfrak {r}})=\sum _{i=1}^{\mathfrak {r}} a_i x_i^2$
, with discriminant
![]() $\Delta (Q_0)=\prod _{i=1}^{\mathfrak {r}} a_i\neq 0$
.
$\Delta (Q_0)=\prod _{i=1}^{\mathfrak {r}} a_i\neq 0$
.
Proposition 3.4. Let
![]() $\ell $
be odd, and let
$\ell $
be odd, and let
![]() $Q(x_1,\dots , x_n)\in \mathbb {F}_q[x_1,\dots , x_n]$
be a quadratic form. Setting
$Q(x_1,\dots , x_n)\in \mathbb {F}_q[x_1,\dots , x_n]$
be a quadratic form. Setting
![]() $\mathfrak {r}:=\operatorname {rank} Q$
, we denote by
$\mathfrak {r}:=\operatorname {rank} Q$
, we denote by
![]() $N(Q=0)$
the number of solutions of
$N(Q=0)$
the number of solutions of
![]() $Q=0$
. Then, we have that
$Q=0$
. Then, we have that
 $$\begin{align*}N(Q=0)=\begin{cases} q^{n-1}+(q-1)q^{n-\mathfrak{r}/2-1}\eta\left((-1)^{\mathfrak{r}/2}\Delta(Q_0)\right),& \text{ if }\mathfrak{r}\text{ is even,}\\ q^{n-1}, & \text{ if }\mathfrak{r}\text{ is odd.}\end{cases}\end{align*}$$
$$\begin{align*}N(Q=0)=\begin{cases} q^{n-1}+(q-1)q^{n-\mathfrak{r}/2-1}\eta\left((-1)^{\mathfrak{r}/2}\Delta(Q_0)\right),& \text{ if }\mathfrak{r}\text{ is even,}\\ q^{n-1}, & \text{ if }\mathfrak{r}\text{ is odd.}\end{cases}\end{align*}$$
Proof. Let
![]() $\mathfrak {r}$
denote the rank of Q, and first consider the case when
$\mathfrak {r}$
denote the rank of Q, and first consider the case when
![]() $\mathfrak {r}$
is even. According to Proposition 3.2, Q is equivalent to a diagonal form. Thus, without loss of generality, assume that there are nonzero constants
$\mathfrak {r}$
is even. According to Proposition 3.2, Q is equivalent to a diagonal form. Thus, without loss of generality, assume that there are nonzero constants
![]() $a_1, \dots , a_{\mathfrak {r}}$
such that
$a_1, \dots , a_{\mathfrak {r}}$
such that
 $$\begin{align*}Q(x_1, \dots, x_{\mathfrak{r}}, \dots, x_n)=\sum_{i=1}^{\mathfrak{r}} a_i x_i^2.\end{align*}$$
$$\begin{align*}Q(x_1, \dots, x_{\mathfrak{r}}, \dots, x_n)=\sum_{i=1}^{\mathfrak{r}} a_i x_i^2.\end{align*}$$
Thus, for every solution to
 $$\begin{align*}Q_0(x_1, \dots, x_{\mathfrak{r}})=\sum_{i=1}^{\mathfrak{r}} a_i x_i^2=0,\end{align*}$$
$$\begin{align*}Q_0(x_1, \dots, x_{\mathfrak{r}})=\sum_{i=1}^{\mathfrak{r}} a_i x_i^2=0,\end{align*}$$
there are
![]() $q^{n-\frak {r}}$
solutions to
$q^{n-\frak {r}}$
solutions to
![]() $Q(x_1, \dots , x_{\mathfrak {r}}, \dots , x_n)=0$
. As a consequence, we find that
$Q(x_1, \dots , x_{\mathfrak {r}}, \dots , x_n)=0$
. As a consequence, we find that
![]() $N(Q=0)=q^{n-\mathfrak {r}} N(Q_0=0)$
. Since
$N(Q=0)=q^{n-\mathfrak {r}} N(Q_0=0)$
. Since
![]() $Q_0$
is nondegenerate, the result follows from Theorem 3.3, according to which
$Q_0$
is nondegenerate, the result follows from Theorem 3.3, according to which
On the other hand, if
![]() $\mathfrak {r}$
is odd, we have that
$\mathfrak {r}$
is odd, we have that
![]() $N(Q_0=0)=q^{\mathfrak {r}-1}$
, according to [Reference Lidl and Niederreiter17, Th. 6.27].
$N(Q_0=0)=q^{\mathfrak {r}-1}$
, according to [Reference Lidl and Niederreiter17, Th. 6.27].
4 Statistics for the Iwasawa invariants of bouquets
Fix an odd prime number
![]() $\ell $
. Recall that a bouquet is a multigraph with a single vertex. As a multigraph, each undirected edge corresponds to a pair of edges oriented in opposite directions, starting and ending at the unique vertex. Thus, in particular, a bouquet is uniquely determined by the number of undirected loops. Let
$\ell $
. Recall that a bouquet is a multigraph with a single vertex. As a multigraph, each undirected edge corresponds to a pair of edges oriented in opposite directions, starting and ending at the unique vertex. Thus, in particular, a bouquet is uniquely determined by the number of undirected loops. Let
![]() $X_t$
be the bouquet with t undirected loops labeled
$X_t$
be the bouquet with t undirected loops labeled
![]() $e_1,\dots , e_t$
. Associated with a vector
$e_1,\dots , e_t$
. Associated with a vector
![]() $\alpha =(\alpha _1,\ldots ,\alpha _t)\in \mathbb {Z}_\ell ^t$
is a
$\alpha =(\alpha _1,\ldots ,\alpha _t)\in \mathbb {Z}_\ell ^t$
is a
![]() $\mathbb {Z}_\ell $
-tower of
$\mathbb {Z}_\ell $
-tower of
![]() $X_t$
. We say that
$X_t$
. We say that
![]() $\alpha $
is admissible if for some coordinate
$\alpha $
is admissible if for some coordinate
![]() $\alpha _i$
, we have that
$\alpha _i$
, we have that
![]() $\ell \nmid \alpha _i$
. Note that according to Corollary 2.16,
$\ell \nmid \alpha _i$
. Note that according to Corollary 2.16,
![]() $\alpha $
is admissible if and only if Assumption 2.6 is satisfied. Let
$\alpha $
is admissible if and only if Assumption 2.6 is satisfied. Let
![]() $\tau =\tau _\ell $
be the Haar measure on
$\tau =\tau _\ell $
be the Haar measure on
![]() $\mathbb {Z}_\ell ^t$
and note that
$\mathbb {Z}_\ell ^t$
and note that
![]() $\tau \left (\mathbb {Z}_\ell ^t\setminus (\ell \mathbb {Z}_\ell )^t\right )=1-\ell ^{-t}$
.
$\tau \left (\mathbb {Z}_\ell ^t\setminus (\ell \mathbb {Z}_\ell )^t\right )=1-\ell ^{-t}$
.
In this section, we study two related questions:
-
1. Given a fixed bouquet
 $X_t$
, how do the Iwasawa invariants
$X_t$
, how do the Iwasawa invariants
 $\mu $
and
$\mu $
and
 $\lambda $
vary, as
$\lambda $
vary, as
 $\alpha =(\alpha _1,\dots , \alpha _t)$
varies over the set of admissible vectors in
$\alpha =(\alpha _1,\dots , \alpha _t)$
varies over the set of admissible vectors in
 $\mathbb {Z}_\ell ^t$
? It follows from Theorem 2.18 that the
$\mathbb {Z}_\ell ^t$
? It follows from Theorem 2.18 that the
 $\lambda $
-invariant for a bouquet is odd. Thus, in particular, the
$\lambda $
-invariant for a bouquet is odd. Thus, in particular, the
 $\lambda $
invariant is
$\lambda $
invariant is
 $\geq 1$
. We fix constants
$\geq 1$
. We fix constants
 $\mu _0\in \mathbb {Z}_{\geq 0}$
and
$\mu _0\in \mathbb {Z}_{\geq 0}$
and
 $\lambda _0\in \mathbb {Z}_{\geq 1}$
, let
$\lambda _0\in \mathbb {Z}_{\geq 1}$
, let
 $\mathcal {S}(\mu _0, \lambda _0,\ell ,t)$
be the set of vectors
$\mathcal {S}(\mu _0, \lambda _0,\ell ,t)$
be the set of vectors
 $\alpha \in \mathbb {Z}_\ell ^t\backslash (\ell \mathbb {Z}_\ell )^t$
such that
$\alpha \in \mathbb {Z}_\ell ^t\backslash (\ell \mathbb {Z}_\ell )^t$
such that
 $\mu _\ell (X_t,\alpha )=\mu _0$
and
$\mu _\ell (X_t,\alpha )=\mu _0$
and
 $\lambda _\ell (X_t,\alpha )=\lambda _0$
. This probability is computed as follows: The above formula does make sense since in the cases of interest, we shall implicitly show that
$\lambda _\ell (X_t,\alpha )=\lambda _0$
. This probability is computed as follows: The above formula does make sense since in the cases of interest, we shall implicitly show that $$ \begin{align*}\operatorname{Prob}_{\ell}\left(X_t; \mu=\mu_0, \lambda=\lambda_0\right):= & \frac{\tau\left(\mathcal{S}(\mu_0, \lambda_0,\ell,t)\right)}{\tau\left(\mathbb{Z}_\ell^t\setminus (\ell \mathbb{Z}_\ell)^t\right)}\\ = & (1-\ell^{-t})^{-1}\tau\left(\mathcal{S}(\mu_0, \lambda_0,\ell,t)\right).\end{align*} $$
$$ \begin{align*}\operatorname{Prob}_{\ell}\left(X_t; \mu=\mu_0, \lambda=\lambda_0\right):= & \frac{\tau\left(\mathcal{S}(\mu_0, \lambda_0,\ell,t)\right)}{\tau\left(\mathbb{Z}_\ell^t\setminus (\ell \mathbb{Z}_\ell)^t\right)}\\ = & (1-\ell^{-t})^{-1}\tau\left(\mathcal{S}(\mu_0, \lambda_0,\ell,t)\right).\end{align*} $$
 $\mathcal {S}(\mu _0, \lambda _0,\ell ,t)$
is measurable. Our computations are possible for certain values of
$\mathcal {S}(\mu _0, \lambda _0,\ell ,t)$
is measurable. Our computations are possible for certain values of
 $\mu _0$
and
$\mu _0$
and
 $\lambda _0$
. The probabilities
$\lambda _0$
. The probabilities
 $\operatorname {Prob}_{\ell }(X_t; \mu>\mu _0)$
,
$\operatorname {Prob}_{\ell }(X_t; \mu>\mu _0)$
,
 $\operatorname {Prob}_{\ell }(X_t; \mu =\mu _0)$
,
$\operatorname {Prob}_{\ell }(X_t; \mu =\mu _0)$
,
 $\operatorname {Prob}_{\ell }(X_t; \mu =\mu _0, \lambda \geq \lambda _0),$
etc. are defined similarly.
$\operatorname {Prob}_{\ell }(X_t; \mu =\mu _0, \lambda \geq \lambda _0),$
etc. are defined similarly.
-
2. Let
 $\mathcal {T}(\mu _0, \lambda _0, \ell )$
be the set of pairs
$\mathcal {T}(\mu _0, \lambda _0, \ell )$
be the set of pairs
 $(t, \alpha )$
, where
$(t, \alpha )$
, where
 $t\in \mathbb {Z}_{\geq 2}$
and admissible
$t\in \mathbb {Z}_{\geq 2}$
and admissible
 $\alpha =(\alpha _1,\dots , \alpha _t)\in \mathbb {Z}^t$
such that
$\alpha =(\alpha _1,\dots , \alpha _t)\in \mathbb {Z}^t$
such that
 $\mu _\ell (X_t, \alpha )=\mu _0$
and
$\mu _\ell (X_t, \alpha )=\mu _0$
and
 $\lambda _\ell (X_t, \alpha )=\lambda _0$
. Fix
$\lambda _\ell (X_t, \alpha )=\lambda _0$
. Fix
 $\delta \in (0,1),$
and let
$\delta \in (0,1),$
and let
 $\mathcal {T}_{\leq x}(\mu _0, \lambda _0, \ell )$
be the set of
$\mathcal {T}_{\leq x}(\mu _0, \lambda _0, \ell )$
be the set of
 $(t,\alpha )\in \mathcal {T}(\mu _0, \lambda _0, \ell )$
such that
$(t,\alpha )\in \mathcal {T}(\mu _0, \lambda _0, \ell )$
such that
 $t\leq x^\delta $
and
$t\leq x^\delta $
and
 $\operatorname {max}\{ |\alpha _1|,\dots , |\alpha _t|\}\leq x$
. Let
$\operatorname {max}\{ |\alpha _1|,\dots , |\alpha _t|\}\leq x$
. Let
 $\mathcal {A}_{\leq x}(\ell )$
be the tuples
$\mathcal {A}_{\leq x}(\ell )$
be the tuples
 $(t,\alpha )$
for which
$(t,\alpha )$
for which
 $\alpha $
is admissible and such that
$\alpha $
is admissible and such that
 $t\leq x^\delta $
and
$t\leq x^\delta $
and
 $\operatorname {max}\{ |\alpha _1|,\dots , |\alpha _t|\}\leq x$
. The density of
$\operatorname {max}\{ |\alpha _1|,\dots , |\alpha _t|\}\leq x$
. The density of
 $\mathcal {T}_{\leq x}(\mu _0, \lambda _0, \ell )$
is given by provided the above limit exists.
$\mathcal {T}_{\leq x}(\mu _0, \lambda _0, \ell )$
is given by provided the above limit exists. $$\begin{align*}\mathfrak{d}_{\ell}(\mu_0, \lambda_0):=\lim_{x\rightarrow \infty} \left(\frac{\# \mathcal{T}_{\leq x}(\mu_0, \lambda_0, \ell)}{\#\mathcal{A}_{\leq x}(\ell)}\right),\end{align*}$$
$$\begin{align*}\mathfrak{d}_{\ell}(\mu_0, \lambda_0):=\lim_{x\rightarrow \infty} \left(\frac{\# \mathcal{T}_{\leq x}(\mu_0, \lambda_0, \ell)}{\#\mathcal{A}_{\leq x}(\ell)}\right),\end{align*}$$
4.1 The vanishing of the
 $\mu $
-invariant
$\mu $
-invariant
In this section, we study when the
![]() $\mu $
-invariant of a
$\mu $
-invariant of a
![]() $\mathbb {Z}_\ell $
-tower of a bouquet
$\mathbb {Z}_\ell $
-tower of a bouquet
![]() $X_t$
vanishes. We are interested in the power series
$X_t$
vanishes. We are interested in the power series
 $$ \begin{align} f(T)=f_{X_t,\alpha}(T)=\sum_{k=1}^tf_{\alpha_k}(T)\in\mathbb{Z}_\ell[\![ T]\!], \end{align} $$
$$ \begin{align} f(T)=f_{X_t,\alpha}(T)=\sum_{k=1}^tf_{\alpha_k}(T)\in\mathbb{Z}_\ell[\![ T]\!], \end{align} $$
where we recall that
 $$\begin{align*}f_{a}(T)=2-(1+T)^{a}-(1+T)^{-a}=-\sum_{n\ge2}\left(\binom{a}{n}+\binom{-a}{n}\right)T^n. \end{align*}$$
$$\begin{align*}f_{a}(T)=2-(1+T)^{a}-(1+T)^{-a}=-\sum_{n\ge2}\left(\binom{a}{n}+\binom{-a}{n}\right)T^n. \end{align*}$$
Upon expanding the binomial coefficients, we deduce that the coefficient of
![]() $T^n$
in
$T^n$
in
![]() $f_a(T)$
is of the form
$f_a(T)$
is of the form
 $$\begin{align*}\frac{2}{n!}\sum_{i=1}^{\lfloor n/2\rfloor}c_{n,i}a^{2i}, \end{align*}$$
$$\begin{align*}\frac{2}{n!}\sum_{i=1}^{\lfloor n/2\rfloor}c_{n,i}a^{2i}, \end{align*}$$
where
![]() $c_{n,i}\in \mathbb {Z}$
is independent of a. More precisely,
$c_{n,i}\in \mathbb {Z}$
is independent of a. More precisely,
![]() $c_{n,i}$
is the coefficient of
$c_{n,i}$
is the coefficient of
![]() $x^{2i}$
in
$x^{2i}$
in
![]() $-x(x-1) \dots (x-n+1)$
. Furthermore, if
$-x(x-1) \dots (x-n+1)$
. Furthermore, if
![]() $n=2m$
is even, then the highest term in a is
$n=2m$
is even, then the highest term in a is
![]() $a^{2m}$
with coefficient
$a^{2m}$
with coefficient
![]() $c_{2m, m}=- 1$
, whereas if
$c_{2m, m}=- 1$
, whereas if
![]() $n=2m+1$
is odd, then the highest term is
$n=2m+1$
is odd, then the highest term is
![]() $a^{2m}$
with coefficient
$a^{2m}$
with coefficient
![]() $c_{2m+1,m}=m(2m+1)$
. We write
$c_{2m+1,m}=m(2m+1)$
. We write
![]() $f(T)=\sum _{n\geq 2} \beta _{n} T^{n}$
, in particular, we have
$f(T)=\sum _{n\geq 2} \beta _{n} T^{n}$
, in particular, we have
 $$\begin{align*}\beta_n=\sum_{k=1}^t\frac{2}{n!}\sum_{i=1}^{\lfloor n/2\rfloor}c_{n,i}\alpha_k^{2i}. \end{align*}$$
$$\begin{align*}\beta_n=\sum_{k=1}^t\frac{2}{n!}\sum_{i=1}^{\lfloor n/2\rfloor}c_{n,i}\alpha_k^{2i}. \end{align*}$$
Lemma 4.1. Let
![]() $\ell $
be an odd prime number, and let
$\ell $
be an odd prime number, and let
![]() $f(T)$
be the power series associated with the
$f(T)$
be the power series associated with the
![]() $\mathbb {Z}_{\ell }$
-tower of the bouquet
$\mathbb {Z}_{\ell }$
-tower of the bouquet
![]() $X_t$
given by the admissible vector
$X_t$
given by the admissible vector
![]() $\alpha =(\alpha _1, \dots , \alpha _t)$
. Suppose that the associated
$\alpha =(\alpha _1, \dots , \alpha _t)$
. Suppose that the associated
![]() $\mu $
-invariant
$\mu $
-invariant
![]() $\mu _\ell (X_t, \alpha )$
is positive. Then, for all
$\mu _\ell (X_t, \alpha )$
is positive. Then, for all
![]() $m\geq 1$
, we have that
$m\geq 1$
, we have that
 $$\begin{align*}\sum_{k} \alpha_k^{2m}\equiv 0 \bmod{\ell^{\mu}}.\end{align*}$$
$$\begin{align*}\sum_{k} \alpha_k^{2m}\equiv 0 \bmod{\ell^{\mu}}.\end{align*}$$
Proof. If
![]() $\mu>0$
, then, all coefficients
$\mu>0$
, then, all coefficients
![]() $\beta _n$
are divisible by
$\beta _n$
are divisible by
![]() $\ell ^{\mu }$
. Setting
$\ell ^{\mu }$
. Setting
![]() $p_i:=\sum _{k} \alpha _k^{2i}$
, we find that
$p_i:=\sum _{k} \alpha _k^{2i}$
, we find that
 $$\begin{align*}\beta_n=\frac{2}{n!}\sum_{i=1}^{\lfloor n/2\rfloor} c_{n, i} p_i\equiv 0 \bmod{\ell^{\mu}}.\end{align*}$$
$$\begin{align*}\beta_n=\frac{2}{n!}\sum_{i=1}^{\lfloor n/2\rfloor} c_{n, i} p_i\equiv 0 \bmod{\ell^{\mu}}.\end{align*}$$
Then, we find that
![]() $\sum _{i=1}^{\lfloor n/2\rfloor } c_{n, i} p_i\equiv 0\bmod {\ell ^{\mu }}$
. Set
$\sum _{i=1}^{\lfloor n/2\rfloor } c_{n, i} p_i\equiv 0\bmod {\ell ^{\mu }}$
. Set
![]() $n=2m$
, and obtain from the above that
$n=2m$
, and obtain from the above that
 $$\begin{align*}p_m=-c_{2m, m}p_m\equiv \sum_{i=1}^{m-1} c_{2m, i} p_i\bmod{\ell^{\mu}}.\end{align*}$$
$$\begin{align*}p_m=-c_{2m, m}p_m\equiv \sum_{i=1}^{m-1} c_{2m, i} p_i\bmod{\ell^{\mu}}.\end{align*}$$
Therefore, by induction on m, we find that
![]() $p_m\equiv 0\bmod {\ell ^\mu }$
for all m.
$p_m\equiv 0\bmod {\ell ^\mu }$
for all m.
Next, we prove a result on the
![]() $\mu $
-invariant. Note that since
$\mu $
-invariant. Note that since
![]() $\alpha $
is assumed to be admissible, we have that
$\alpha $
is assumed to be admissible, we have that
![]() $\#\{k:\alpha _k\not \equiv 0\bmod \ell \}>0$
.
$\#\{k:\alpha _k\not \equiv 0\bmod \ell \}>0$
.
Proposition 4.2. Assume that
![]() $\ell $
is odd. If
$\ell $
is odd. If
![]() $\mu>0$
, then
$\mu>0$
, then
![]() $\#\{k:\alpha _k\not \equiv 0\bmod \ell \}$
is a multiple of
$\#\{k:\alpha _k\not \equiv 0\bmod \ell \}$
is a multiple of
![]() $\ell $
.
$\ell $
.
Proof. Let us write
![]() $p_i:=\sum _{k=1}^t\alpha _k^{2i}$
. By Lemma 4.1, we find that
$p_i:=\sum _{k=1}^t\alpha _k^{2i}$
. By Lemma 4.1, we find that
![]() $p_i\equiv 0\bmod \ell ^{\mu }$
for all
$p_i\equiv 0\bmod \ell ^{\mu }$
for all
![]() $i\ge 1$
.
$i\ge 1$
.
Let us write
![]() $N=\#\{k:\alpha _k\not \equiv 0\bmod \ell \}$
. For
$N=\#\{k:\alpha _k\not \equiv 0\bmod \ell \}$
. For
![]() $1\le i\le N$
, let
$1\le i\le N$
, let
![]() $p_i'$
denote the power sum
$p_i'$
denote the power sum
 $\displaystyle \sum _{\ell \nmid \alpha _k}\alpha _k^{2i}$
and let
$\displaystyle \sum _{\ell \nmid \alpha _k}\alpha _k^{2i}$
and let
![]() $e_i$
denote the symmetric sum
$e_i$
denote the symmetric sum
 $\displaystyle \sum _{k_1<\cdots <k_i} \alpha _{k_1}^2\ldots \alpha _{k_i}^2$
of the same elements. In particular,
$\displaystyle \sum _{k_1<\cdots <k_i} \alpha _{k_1}^2\ldots \alpha _{k_i}^2$
of the same elements. In particular,
![]() $p_i'\equiv 0\bmod \ell $
for all i. Newton’s identities (see [Reference Mead21]) say that
$p_i'\equiv 0\bmod \ell $
for all i. Newton’s identities (see [Reference Mead21]) say that
 $$\begin{align*}ie_i=\sum_{j=1}^i(-1)^{j-1}e_{i-j}p'_j,\quad 1\le i\le N, \end{align*}$$
$$\begin{align*}ie_i=\sum_{j=1}^i(-1)^{j-1}e_{i-j}p'_j,\quad 1\le i\le N, \end{align*}$$
where
![]() $e_0$
is defined to be
$e_0$
is defined to be
![]() $1$
. In particular,
$1$
. In particular,
![]() $Ne_N\equiv 0\bmod \ell $
. By definition,
$Ne_N\equiv 0\bmod \ell $
. By definition,
 $$ \begin{align*}e_N=\prod_{\ell\nmid \alpha_k}\alpha_k^2\not\equiv 0\bmod \ell.\end{align*} $$
$$ \begin{align*}e_N=\prod_{\ell\nmid \alpha_k}\alpha_k^2\not\equiv 0\bmod \ell.\end{align*} $$
Thus, we deduce that
![]() $\ell |N$
.
$\ell |N$
.
The result below improves upon (see [Reference Vallières26, Cor. 5.8]).
Corollary 4.3. Let
![]() $\ell $
be an odd prime. If
$\ell $
be an odd prime. If
![]() $t<\ell $
, then
$t<\ell $
, then
![]() $\mu =0$
.
$\mu =0$
.
Proof. Note that since there exists some value
![]() $\alpha _k$
such that
$\alpha _k$
such that
![]() $\ell \nmid \alpha _k$
, we find that
$\ell \nmid \alpha _k$
, we find that
![]() $\#\{k:\alpha _k\not \equiv 0\bmod \ell \}>0$
. According to Proposition 4.2,
$\#\{k:\alpha _k\not \equiv 0\bmod \ell \}>0$
. According to Proposition 4.2,
and the result follows.
The following result is a refinement of Proposition 4.2.
Proposition 4.4. Let
![]() $\ell $
be an odd prime, and suppose that
$\ell $
be an odd prime, and suppose that
![]() $\mu>0$
. Let
$\mu>0$
. Let
![]() $Q_\ell $
be the set of nonzero quadratic residues modulo
$Q_\ell $
be the set of nonzero quadratic residues modulo
![]() $\ell $
. For each
$\ell $
. For each
![]() $x\in Q_\ell $
, let
$x\in Q_\ell $
, let
![]() $r_x:=\#\{\alpha _k:\alpha _k^2\equiv x\bmod \ell \}$
. Then
$r_x:=\#\{\alpha _k:\alpha _k^2\equiv x\bmod \ell \}$
. Then
![]() $r_x\equiv 0\bmod \ell ^{\mu }$
for all
$r_x\equiv 0\bmod \ell ^{\mu }$
for all
![]() $x\in Q_\ell $
.
$x\in Q_\ell $
.
Proof. Recall from the proof Proposition 4.2 that we have
 $$\begin{align*}\sum_{k=1}^t \alpha_k^{2i}\equiv0\bmod \ell^{\mu},\quad i\ge 1. \end{align*}$$
$$\begin{align*}\sum_{k=1}^t \alpha_k^{2i}\equiv0\bmod \ell^{\mu},\quad i\ge 1. \end{align*}$$
This implies that
 $$\begin{align*}\sum_{x\in Q_\ell} r_x \cdot x^{i}\equiv 0\bmod\ell^{\mu}, \quad i=1,\ldots, (\ell-1)/2. \end{align*}$$
$$\begin{align*}\sum_{x\in Q_\ell} r_x \cdot x^{i}\equiv 0\bmod\ell^{\mu}, \quad i=1,\ldots, (\ell-1)/2. \end{align*}$$
The determinant of the Vandermonde matrix
![]() $(x^i)_{x\in Q_\ell ,1\le i\le (\ell -1)/2}$
is nonzero mod
$(x^i)_{x\in Q_\ell ,1\le i\le (\ell -1)/2}$
is nonzero mod
![]() $\ell $
. Therefore, we deduce that
$\ell $
. Therefore, we deduce that
![]() $r_x\equiv 0\bmod \ell ^{\mu }$
for all x.
$r_x\equiv 0\bmod \ell ^{\mu }$
for all x.
Remark 4.5. The converse to the statement in Proposition 4.4 is not true. For instance, let
![]() $\ell =t=3$
and
$\ell =t=3$
and
![]() $\alpha =(1,1,2)$
, we find that
$\alpha =(1,1,2)$
, we find that
 $$ \begin{align*}f(T)=& 2\left(2-(1+T)-(1+T)^{-1}\right)+\left(2-(1+T)^2-(1+T)^{-2}\right)\\ \equiv & \frac{2T^4}{(T + 1)^2}\bmod{3}.\end{align*} $$
$$ \begin{align*}f(T)=& 2\left(2-(1+T)-(1+T)^{-1}\right)+\left(2-(1+T)^2-(1+T)^{-2}\right)\\ \equiv & \frac{2T^4}{(T + 1)^2}\bmod{3}.\end{align*} $$
In particular, the
![]() $\mu $
-invariant is zero. This also gives a counterexample for the converse of both Lemma 4.1 and Proposition 4.2.
$\mu $
-invariant is zero. This also gives a counterexample for the converse of both Lemma 4.1 and Proposition 4.2.
Theorem 4.6. Suppose that
![]() $\ell $
is odd, and let
$\ell $
is odd, and let
![]() $m=(\ell -1)/2$
. We have
$m=(\ell -1)/2$
. We have
 $$\begin{align*}\operatorname{Prob}_{\ell}(X_t;\mu>0)\le \sum_{i=1}^{\lfloor t/\ell\rfloor }2^{i\ell}\binom{t}{i\ell}\sum_{a_1+\cdots+a_m=i}\frac{(i\ell)!}{\prod_{i=1}^m(a_j\ell)!(\ell^t-1)}, \end{align*}$$
$$\begin{align*}\operatorname{Prob}_{\ell}(X_t;\mu>0)\le \sum_{i=1}^{\lfloor t/\ell\rfloor }2^{i\ell}\binom{t}{i\ell}\sum_{a_1+\cdots+a_m=i}\frac{(i\ell)!}{\prod_{i=1}^m(a_j\ell)!(\ell^t-1)}, \end{align*}$$
where the second sum runs over nonnegative integers
![]() $a_j\ge 0$
.
$a_j\ge 0$
.
Proof. If
![]() $\mu>0$
, then Proposition 4.2 tells us that
$\mu>0$
, then Proposition 4.2 tells us that
![]() $\#\{k:\alpha _k\not \equiv 0\bmod \ell \}$
is a multiple of
$\#\{k:\alpha _k\not \equiv 0\bmod \ell \}$
is a multiple of
![]() $\ell $
. Since each residue class modulo
$\ell $
. Since each residue class modulo
![]() $\ell $
in
$\ell $
in
![]() $\alpha \in \mathbb {Z}_\ell ^t\setminus (\ell \mathbb {Z}_\ell )^t$
has the same measure, it is enough to count the number of elements in
$\alpha \in \mathbb {Z}_\ell ^t\setminus (\ell \mathbb {Z}_\ell )^t$
has the same measure, it is enough to count the number of elements in
![]() $(r_1,\ldots , r_t)\in \mathbb {F}_\ell ^t\setminus \{0\}$
such that
$(r_1,\ldots , r_t)\in \mathbb {F}_\ell ^t\setminus \{0\}$
such that
![]() $\#\{k:r_k\neq 0\}$
is a multiple of
$\#\{k:r_k\neq 0\}$
is a multiple of
![]() $\ell $
and
$\ell $
and
![]() $\sum _{k=1}^t r_k^{2i}= 0$
, for all
$\sum _{k=1}^t r_k^{2i}= 0$
, for all
![]() $i\ge 1$
.
$i\ge 1$
.
For each
![]() $1\le i\le \lfloor t/\ell \rfloor $
, we may choose
$1\le i\le \lfloor t/\ell \rfloor $
, we may choose
![]() $i\ell $
indices
$i\ell $
indices
![]() $k_1,\dots , k_{i\ell }$
so that
$k_1,\dots , k_{i\ell }$
so that
![]() $r_j\neq 0$
if and only if
$r_j\neq 0$
if and only if
![]() $j\in \{k_b\mid b=1,\dots , i\ell \}$
. By Proposition 4.4, amongst these
$j\in \{k_b\mid b=1,\dots , i\ell \}$
. By Proposition 4.4, amongst these
![]() $i\ell $
elements, we have to distribute
$i\ell $
elements, we have to distribute
![]() $r_j^2$
over the m classes in
$r_j^2$
over the m classes in
![]() $Q_\ell $
so that the number of times each quadratic residue occurs is a multiple of
$Q_\ell $
so that the number of times each quadratic residue occurs is a multiple of
![]() $\ell $
.
$\ell $
.
Let
![]() $a_1\ell ,\ldots ,a_{m}\ell $
be the number of times the residue classes in
$a_1\ell ,\ldots ,a_{m}\ell $
be the number of times the residue classes in
![]() $Q_\ell $
occur. We have
$Q_\ell $
occur. We have
There are
![]() $(i\ell )!/\prod _{i=1}^m(a_j\ell )!$
ways to distribute
$(i\ell )!/\prod _{i=1}^m(a_j\ell )!$
ways to distribute
![]() $i\ell $
distinguishable elements in m distinguishable sets so that the number of elements in these sets are given by
$i\ell $
distinguishable elements in m distinguishable sets so that the number of elements in these sets are given by
![]() $a_1\ell ,\ldots ,a_m\ell $
. Once we have distributed the
$a_1\ell ,\ldots ,a_m\ell $
. Once we have distributed the
![]() $i\ell $
elements amongst the m classes, each element has two possible values modulo
$i\ell $
elements amongst the m classes, each element has two possible values modulo
![]() $\ell $
, giving us
$\ell $
, giving us
![]() $2^{i\ell }$
choices. Summing up all possible choices of
$2^{i\ell }$
choices. Summing up all possible choices of
![]() $a_j$
’s gives the expression on the right-hand side of the inequality.
$a_j$
’s gives the expression on the right-hand side of the inequality.
Remark 4.7. Our numerical calculations suggest that for a given
![]() $\ell $
, the right-hand side of the inequality given by Theorem 4.6 tends to
$\ell $
, the right-hand side of the inequality given by Theorem 4.6 tends to
![]() $\frac {1}{\ell ^{(\ell -1)/2}}$
as
$\frac {1}{\ell ^{(\ell -1)/2}}$
as
![]() $t\rightarrow \infty $
.
$t\rightarrow \infty $
.

In what follows, we prove a necessary and sufficient condition for
![]() $\mu>0$
in the special case where
$\mu>0$
in the special case where
![]() $\alpha _k\in \mathbb {Z}$
for all k. Given an integer
$\alpha _k\in \mathbb {Z}$
for all k. Given an integer
![]() $a\in \mathbb {Z}$
, let us write
$a\in \mathbb {Z}$
, let us write
![]() $d_k(a)$
for the coefficient of
$d_k(a)$
for the coefficient of
![]() $X^k$
in the shifted Chebyshev polynomial
$X^k$
in the shifted Chebyshev polynomial
![]() $P_a(X)$
used in [Reference McGown and Vallières19, Sec. 2]. More explicitly,
$P_a(X)$
used in [Reference McGown and Vallières19, Sec. 2]. More explicitly,
where the Chebyshev polynomials
![]() $T_a(X)\in \mathbb {Z}[X]$
of the first kind are defined by the relation
$T_a(X)\in \mathbb {Z}[X]$
of the first kind are defined by the relation
for all
![]() $\theta \in \mathbb {R}$
(see [Reference McGown and Vallières19, Sec. 2]).
$\theta \in \mathbb {R}$
(see [Reference McGown and Vallières19, Sec. 2]).
Lemma 4.8. Let
![]() $m\ge 1$
be an integer. Let
$m\ge 1$
be an integer. Let
![]() $b_{1},\ldots ,b_{m}$
be distinct positive integers, then
$b_{1},\ldots ,b_{m}$
be distinct positive integers, then
Proof. Indeed, if we list the
![]() $b_{i}$
in increasing order, then the matrix
$b_{i}$
in increasing order, then the matrix
![]() $(d_{b_{i}}(b_{j}))$
is upper-triangular with
$(d_{b_{i}}(b_{j}))$
is upper-triangular with
![]() $\pm 1$
on the diagonal, since
$\pm 1$
on the diagonal, since
![]() $d_{n}(n) = (-1)^{n-1}$
for all
$d_{n}(n) = (-1)^{n-1}$
for all
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Proposition 4.9. Let
![]() $\alpha :S \to \mathbb {Z}$
be a function for which there exists at least one
$\alpha :S \to \mathbb {Z}$
be a function for which there exists at least one
![]() $s \in S$
such that
$s \in S$
such that
![]() $(\alpha (s),\ell )=1$
. Let
$(\alpha (s),\ell )=1$
. Let
![]() $b_{1},\ldots ,b_{m}$
be the nonzero distinct elements of the set
$b_{1},\ldots ,b_{m}$
be the nonzero distinct elements of the set
![]() $\{|\alpha (s)|: s \in S\}$
. For
$\{|\alpha (s)|: s \in S\}$
. For
![]() $j=1,\ldots ,m$
, let
$j=1,\ldots ,m$
, let
![]() $t_{j} = \#\{s \in S : |\alpha (s)|=b_{j} \}$
. Then, the polynomial
$t_{j} = \#\{s \in S : |\alpha (s)|=b_{j} \}$
. Then, the polynomial
![]() $\sum _{s\in S}P_{\alpha (s)}(X)$
belongs to
$\sum _{s\in S}P_{\alpha (s)}(X)$
belongs to
![]() $\ell \mathbb {Z}[X]$
if and only if
$\ell \mathbb {Z}[X]$
if and only if
![]() $\ell \, | \, t_{j}$
for all
$\ell \, | \, t_{j}$
for all
![]() $j=1,\ldots ,m$
.
$j=1,\ldots ,m$
.
Proof. We have
![]() $P_{a}(X) = P_{-a}(X)$
for all
$P_{a}(X) = P_{-a}(X)$
for all
![]() $a \in \mathbb {Z}$
. Thus,
$a \in \mathbb {Z}$
. Thus,
 $$ \begin{align} \sum_{s\in S}P_{\alpha(s)}(X) = \sum_{j=1}^{m}t_{j}P_{b_{j}}(X). \end{align} $$
$$ \begin{align} \sum_{s\in S}P_{\alpha(s)}(X) = \sum_{j=1}^{m}t_{j}P_{b_{j}}(X). \end{align} $$
It is clear that
![]() $\ell \, | \, t_{j}$
for all
$\ell \, | \, t_{j}$
for all
![]() $j=1,\ldots ,m$
implies that the polynomial above belongs to
$j=1,\ldots ,m$
implies that the polynomial above belongs to
![]() $ \ell \mathbb {Z}[X]$
.
$ \ell \mathbb {Z}[X]$
.
Conversely, if
![]() $\sum _{s\in S}P_{\alpha (s)}(X) \in \ell \mathbb {Z}[X]$
, then (4.2) implies that
$\sum _{s\in S}P_{\alpha (s)}(X) \in \ell \mathbb {Z}[X]$
, then (4.2) implies that
 $$ \begin{align} \sum_{j=1}^{m}d_{k}(b_{j})t_{j} \equiv 0\quad \pmod{\ell} \end{align} $$
$$ \begin{align} \sum_{j=1}^{m}d_{k}(b_{j})t_{j} \equiv 0\quad \pmod{\ell} \end{align} $$
for all
![]() $k \ge 1$
. If we let b be the maximal value of the
$k \ge 1$
. If we let b be the maximal value of the
![]() $b_{j}$
, then the matrix
$b_{j}$
, then the matrix
![]() $(d_{k}(b_{j}) + \ell \mathbb {Z}) \in M_{b\times m}(\mathbb {F}_{\ell })$
has rank m over
$(d_{k}(b_{j}) + \ell \mathbb {Z}) \in M_{b\times m}(\mathbb {F}_{\ell })$
has rank m over
![]() $\mathbb {F}_{\ell }$
by Lemma 4.8. Therefore, the system of linear equations (4.3) has a unique solution modulo
$\mathbb {F}_{\ell }$
by Lemma 4.8. Therefore, the system of linear equations (4.3) has a unique solution modulo
![]() $\ell $
. This tells us that
$\ell $
. This tells us that
![]() $\ell \, | \, t_{j}$
for all
$\ell \, | \, t_{j}$
for all
![]() $j=1,\ldots ,m$
and concludes the proof.
$j=1,\ldots ,m$
and concludes the proof.
Corollary 4.10. Let
![]() $b_1,\ldots ,b_m$
be the nonzero distinct elements of the set
$b_1,\ldots ,b_m$
be the nonzero distinct elements of the set
![]() $\{|\alpha (s)|: s\in S\}$
and write
$\{|\alpha (s)|: s\in S\}$
and write
![]() $t_j=\#\{s\in S:|\alpha (s)|=b_j\}$
for
$t_j=\#\{s\in S:|\alpha (s)|=b_j\}$
for
![]() $j=1,\ldots , m$
. Then
$j=1,\ldots , m$
. Then
![]() $\mu _\ell (X_t,\alpha )>0$
if and only if
$\mu _\ell (X_t,\alpha )>0$
if and only if
![]() $\ell |t_j$
for all
$\ell |t_j$
for all
![]() $j=1,\ldots ,m$
.
$j=1,\ldots ,m$
.
Proof. By [Reference Vallières26, Th. 5.6],
![]() $\mu _\ell (X_t,\alpha )>0$
if and only if
$\mu _\ell (X_t,\alpha )>0$
if and only if
![]() $\sum _{s\in S}P_{\alpha (s)}(X)\in \ell \mathbb {Z}[X]$
. Therefore, the result follows from Proposition 4.9.
$\sum _{s\in S}P_{\alpha (s)}(X)\in \ell \mathbb {Z}[X]$
. Therefore, the result follows from Proposition 4.9.
4.2 The distribution of Iwasawa invariants of a fixed
 $X_t$
varying
$X_t$
varying
 $\alpha $
$\alpha $
In this section, we fix an odd prime number
![]() $\ell $
and fix an integer
$\ell $
and fix an integer
![]() $t\geq 2$
. We let
$t\geq 2$
. We let
![]() $X_t$
be the bouquet with t undirected loops and we study question (1). Note that Assumption 2.8 requires that
$X_t$
be the bouquet with t undirected loops and we study question (1). Note that Assumption 2.8 requires that
![]() $\chi (X_{t})\neq 0$
, and hence, we avoid the case when
$\chi (X_{t})\neq 0$
, and hence, we avoid the case when
![]() $t=1$
(see §4.3 for a separate discussion on this case).
$t=1$
(see §4.3 for a separate discussion on this case).
We begin by considering
![]() $\mathcal {S}(\mu _0, \lambda _0, \ell , t)$
. Throughout, it shall be assumed that
$\mathcal {S}(\mu _0, \lambda _0, \ell , t)$
. Throughout, it shall be assumed that
![]() $\alpha :S\rightarrow \mathbb {Z}_\ell $
is an admissible function. We compute the probability
$\alpha :S\rightarrow \mathbb {Z}_\ell $
is an admissible function. We compute the probability
![]() $\operatorname {Prob}(X_t;\mu =\mu _0,\lambda = \lambda _0)$
for various values of
$\operatorname {Prob}(X_t;\mu =\mu _0,\lambda = \lambda _0)$
for various values of
![]() $(\mu _0, \lambda _0)\in \mathbb {Z}_{\geq 0}\times \mathbb {Z}_{\geq 0}$
. Note that according to Theorem 2.18,
$(\mu _0, \lambda _0)\in \mathbb {Z}_{\geq 0}\times \mathbb {Z}_{\geq 0}$
. Note that according to Theorem 2.18,
![]() $\lambda $
is odd, and thus, the minimal values of
$\lambda $
is odd, and thus, the minimal values of
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
are
$\lambda $
are
![]() $0$
and
$0$
and
![]() $1$
, respectively.
$1$
, respectively.
Lemma 4.11. Suppose that
![]() $\ell $
is a prime number and
$\ell $
is a prime number and
![]() $f(T)$
is the power series defined above (see (4.1)). Then,
$f(T)$
is the power series defined above (see (4.1)). Then,
![]() $\lambda =\lambda _{\ell }(X_t, \alpha )\geq 1$
and the following conditions are equivalent:
$\lambda =\lambda _{\ell }(X_t, \alpha )\geq 1$
and the following conditions are equivalent:
-
1.
 $\mu =0$
and
$\mu =0$
and
 $\lambda =n$
,
$\lambda =n$
, -
2.
 $\ell \mid \beta _i$
for all
$\ell \mid \beta _i$
for all
 $i \leq n$
and
$i \leq n$
and
 $\beta _{n+1}\in \mathbb {Z}_\ell ^\times $
.
$\beta _{n+1}\in \mathbb {Z}_\ell ^\times $
.
Proof. Theorem 2.18 asserts that
![]() $\lambda $
is odd, thus
$\lambda $
is odd, thus
![]() $\lambda \geq 1$
. Alternatively, this may be directly shown as follows. Express
$\lambda \geq 1$
. Alternatively, this may be directly shown as follows. Express
![]() $f(T)$
as
$f(T)$
as
![]() $\ell ^{\mu } \mathcal {P}(T) u(T)$
, where
$\ell ^{\mu } \mathcal {P}(T) u(T)$
, where
![]() $\mathcal {P}(T)$
is a distinguished polynomial and
$\mathcal {P}(T)$
is a distinguished polynomial and
![]() $u(T)$
is a unit in
$u(T)$
is a unit in
![]() $\Lambda $
. Here,
$\Lambda $
. Here,
![]() $\mu =\mu _{\ell }(X_t, a)$
is the
$\mu =\mu _{\ell }(X_t, a)$
is the
![]() $\mu $
-invariant and
$\mu $
-invariant and
![]() $\lambda =\lambda _{\ell }(X_t, a)=\operatorname {deg} \mathcal {P}-1$
. Note that since
$\lambda =\lambda _{\ell }(X_t, a)=\operatorname {deg} \mathcal {P}-1$
. Note that since
![]() $\beta _i=0$
for
$\beta _i=0$
for
![]() $i\leq 2$
, it follows that
$i\leq 2$
, it follows that
![]() $T^2$
divides
$T^2$
divides
![]() $\mathcal {P}(T)$
, and thus
$\mathcal {P}(T)$
, and thus
![]() $\operatorname {deg} \mathcal {P}(T)\geq 2$
and
$\operatorname {deg} \mathcal {P}(T)\geq 2$
and
![]() $\lambda \geq 1$
.
$\lambda \geq 1$
.
Since
![]() $T^2$
divides
$T^2$
divides
![]() $\mathcal {P}(T)$
, we have that
$\mathcal {P}(T)$
, we have that
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =1$
, if and only if
$\lambda =1$
, if and only if
![]() $f(T)=T^2u(T)$
, where
$f(T)=T^2u(T)$
, where
![]() $u(T)$
is a unit in
$u(T)$
is a unit in
![]() $\Lambda $
. This is the case precisely when
$\Lambda $
. This is the case precisely when
![]() $\beta _2$
is a unit in
$\beta _2$
is a unit in
![]() $\mathbb {Z}_{\ell }$
. More generally, if
$\mathbb {Z}_{\ell }$
. More generally, if
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =n$
, then,
$\lambda =n$
, then,
![]() $f(T)=\mathcal {P}(T) u(T)$
. Reducing modulo
$f(T)=\mathcal {P}(T) u(T)$
. Reducing modulo
![]() $\ell $
, we find that
$\ell $
, we find that
![]() $\mathcal {P}(T)\equiv T^{n+1}\bmod \ell $
, whereby,
$\mathcal {P}(T)\equiv T^{n+1}\bmod \ell $
, whereby,
![]() $\ell \mid \beta _i$
for
$\ell \mid \beta _i$
for
![]() $i\leq n$
and
$i\leq n$
and
![]() $\beta _{n+1}\in \mathbb {Z}_\ell ^{\times }$
. The converse follows from the same argument.
$\beta _{n+1}\in \mathbb {Z}_\ell ^{\times }$
. The converse follows from the same argument.
Lemma 4.12. Let
![]() $\ell $
be an odd prime number, set
$\ell $
be an odd prime number, set
![]() $\mu =\mu _\ell (X_t, \alpha )$
and
$\mu =\mu _\ell (X_t, \alpha )$
and
![]() $\lambda =\lambda _\ell (X_t, \alpha )$
. Then, the following assertions hold.
$\lambda =\lambda _\ell (X_t, \alpha )$
. Then, the following assertions hold.
-
1. Suppose that k is an integer such that
 $0<2k<\ell $
. Then, the following assertions are equivalent:
$0<2k<\ell $
. Then, the following assertions are equivalent:-
(a)
 $\mu =0$
and
$\mu =0$
and
 $\lambda =2k-1$
,
$\lambda =2k-1$
, -
(b) for all
 $i<k$
, and
$i<k$
, and $$\begin{align*}\sum_{j=1}^t \alpha_j^{2i}\equiv 0\bmod{\ell}\end{align*}$$
$$\begin{align*}\sum_{j=1}^t \alpha_j^{2i}\equiv 0\bmod{\ell}\end{align*}$$
 $$\begin{align*}\sum_{j=1}^t \alpha_j^{2k}\not\equiv 0\bmod{\ell}.\end{align*}$$
$$\begin{align*}\sum_{j=1}^t \alpha_j^{2k}\not\equiv 0\bmod{\ell}.\end{align*}$$
-
-
2. If
 $2k\geq \ell $
,
$2k\geq \ell $
,
 $\mu =0$
and
$\mu =0$
and
 $\lambda =2k-1$
, then for all
$\lambda =2k-1$
, then for all
 $i<k$
,
$i<k$
,  $$\begin{align*}\sum_{j=1}^t \alpha_j^{2i}\equiv 0\bmod{\ell}.\end{align*}$$
$$\begin{align*}\sum_{j=1}^t \alpha_j^{2i}\equiv 0\bmod{\ell}.\end{align*}$$
Proof. First, assume that
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =2k-1$
. Setting
$\lambda =2k-1$
. Setting
![]() $p_i:=\sum _{j} \alpha _j^{2i}$
, we find that
$p_i:=\sum _{j} \alpha _j^{2i}$
, we find that
 $$\begin{align*}\beta_n=\frac{2}{n!}\sum_{i=1}^{\lfloor n/2\rfloor} c_{n, i} p_i.\end{align*}$$
$$\begin{align*}\beta_n=\frac{2}{n!}\sum_{i=1}^{\lfloor n/2\rfloor} c_{n, i} p_i.\end{align*}$$
According to Lemma 4.11,
![]() $\beta _n$
is divisible by
$\beta _n$
is divisible by
![]() $\ell $
for all values of
$\ell $
for all values of
![]() $n<2k$
, and
$n<2k$
, and
![]() $\beta _{2k}$
is not divisible by
$\beta _{2k}$
is not divisible by
![]() $\ell $
. The assertion of part (2) follows immediately from this.
$\ell $
. The assertion of part (2) follows immediately from this.
We now prove (1). In particular, we assume that
![]() $2k<\ell $
. Then,
$2k<\ell $
. Then,
![]() $\frac {2}{n!}$
is an
$\frac {2}{n!}$
is an
![]() $\ell $
-adic unit for all integers n such that
$\ell $
-adic unit for all integers n such that
![]() $0\le n\leq 2k$
.
$0\le n\leq 2k$
.
Suppose that (b) holds. Then,
![]() $p_i$
is divisible by
$p_i$
is divisible by
![]() $\ell $
for all
$\ell $
for all
![]() $i<k$
, whereas
$i<k$
, whereas
![]() $p_k$
is not divisible by
$p_k$
is not divisible by
![]() $\ell $
. It follows that
$\ell $
. It follows that
![]() $\ell $
divides
$\ell $
divides
![]() $\beta _n$
for all
$\beta _n$
for all
![]() $n<2k$
, but
$n<2k$
, but
![]() $\beta _{2k}$
is not divisible by
$\beta _{2k}$
is not divisible by
![]() $\ell $
. Thus, (a) holds by Lemma 4.11.
$\ell $
. Thus, (a) holds by Lemma 4.11.
Conversely, suppose that (a) holds. Then
 $$\begin{align*}\ell\ | \sum_{i=1}^{\lfloor n/2\rfloor}c_{n,i}p_i,\ n<2k,\quad \ell \nmid \sum_{i=1}^{k}c_{2k,i}p_i.\end{align*}$$
$$\begin{align*}\ell\ | \sum_{i=1}^{\lfloor n/2\rfloor}c_{n,i}p_i,\ n<2k,\quad \ell \nmid \sum_{i=1}^{k}c_{2k,i}p_i.\end{align*}$$
Recall that
![]() $c_{2m,m}=-1$
for all
$c_{2m,m}=-1$
for all
![]() $m\ge 1$
. An inductive argument shows that
$m\ge 1$
. An inductive argument shows that
![]() $\ell |p_i$
for
$\ell |p_i$
for
![]() $i<k$
, and
$i<k$
, and
![]() $\ell \nmid p_k$
. In particular, (b) holds.
$\ell \nmid p_k$
. In particular, (b) holds.
Theorem 4.13. We let
![]() $\ell $
be an odd prime and
$\ell $
be an odd prime and
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
denote the Iwasawa invariants
$\lambda $
denote the Iwasawa invariants
![]() $\mu _{\ell }(X_t, \alpha )$
and
$\mu _{\ell }(X_t, \alpha )$
and
![]() $\lambda _{\ell }(X_t, \alpha )$
, respectively. If
$\lambda _{\ell }(X_t, \alpha )$
, respectively. If
![]() $\ell>t$
, then
$\ell>t$
, then
![]() $\lambda < 2t$
.
$\lambda < 2t$
.
Proof. By Corollary 4.3,
![]() $\ell>t$
implies that the
$\ell>t$
implies that the
![]() $\mu $
-invariant of
$\mu $
-invariant of
![]() $f(T)$
is zero. Assume by way of contradiction that
$f(T)$
is zero. Assume by way of contradiction that
![]() $\lambda \geq 2t$
. Then,
$\lambda \geq 2t$
. Then,
![]() $\beta _2,\ldots , \beta _{2t}\equiv 0\bmod \ell $
. Under the same notation as in the proof of Proposition 4.2, we have
$\beta _2,\ldots , \beta _{2t}\equiv 0\bmod \ell $
. Under the same notation as in the proof of Proposition 4.2, we have
forcing
![]() $Ne_N\equiv 0\bmod \ell $
once again by Newton’s identities (see [Reference Mead21]). But this is impossible if
$Ne_N\equiv 0\bmod \ell $
once again by Newton’s identities (see [Reference Mead21]). But this is impossible if
![]() $\ell>t$
, proving the affirmation of the theorem.
$\ell>t$
, proving the affirmation of the theorem.
Remark 4.14. Without the condition
![]() $\ell>t$
, it is possible that
$\ell>t$
, it is possible that
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda> 2t$
. In fact, applying Lemma 2.17 with
$\lambda> 2t$
. In fact, applying Lemma 2.17 with
![]() $n_{1}=0$
shows that it is possible to find examples with
$n_{1}=0$
shows that it is possible to find examples with
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda $
arbitrarily large when
$\lambda $
arbitrarily large when
![]() $t = \ell +1$
. When
$t = \ell +1$
. When
![]() $t=\ell =2$
, we have found examples with
$t=\ell =2$
, we have found examples with
![]() $\mu =0$
and
$\mu =0$
and
Whereas when
![]() $t=3$
, for
$t=3$
, for
![]() $\ell =2,$
we have found examples with
$\ell =2,$
we have found examples with
![]() $\mu =0$
and
$\mu =0$
and
and for
![]() $\ell = 3,$
we have found examples with
$\ell = 3,$
we have found examples with
![]() $\mu =0$
and
$\mu =0$
and
For instance, if we take
![]() $t=3$
,
$t=3$
,
![]() $\ell = 3$
, with the voltage assignment on the three edges given by 1, 8, and 10, respectively, then we get:
$\ell = 3$
, with the voltage assignment on the three edges given by 1, 8, and 10, respectively, then we get:

The power series
![]() $f(T)$
starts as follows:
$f(T)$
starts as follows:
where
![]() $3$
divides all the coefficients up to and including
$3$
divides all the coefficients up to and including
![]() $3,470,655$
, but it does not divide
$3,470,655$
, but it does not divide
![]() $5,167,526$
. Thus,
$5,167,526$
. Thus,
![]() $\mu = 0$
and
$\mu = 0$
and
![]() $\lambda = 17$
. Furthermore, since
$\lambda = 17$
. Furthermore, since
 $$ \begin{align*}\log_{3}\left(\frac{3}{2} \cdot 18 \right) = 3,\end{align*} $$
$$ \begin{align*}\log_{3}\left(\frac{3}{2} \cdot 18 \right) = 3,\end{align*} $$
[Reference McGown and Vallières19, Th. 4.1] implies that if
![]() $n \ge 3$
, we have
$n \ge 3$
, we have
for some
![]() $\nu \in \mathbb {Z}$
. Using SageMath [Reference Stein23], we calculate
$\nu \in \mathbb {Z}$
. Using SageMath [Reference Stein23], we calculate
and
Thus, we have
for all
![]() $n \ge 2$
.
$n \ge 2$
.
Remark 4.15. It directly follows from Theorem 4.13 that if
![]() $\ell>t$
, then
$\ell>t$
, then
![]() $\operatorname {Prob}_{\ell }(X_t; \mu =\mu _0, \lambda =\lambda _0)=0$
unless
$\operatorname {Prob}_{\ell }(X_t; \mu =\mu _0, \lambda =\lambda _0)=0$
unless
![]() $\mu _0=0$
and
$\mu _0=0$
and
![]() $\lambda _0< 2t$
.
$\lambda _0< 2t$
.
We wish to estimate the probability
![]() $\operatorname {Prob}_\ell (X_t; \mu =0, \lambda =\lambda _0)$
. Note that by Theorem 2.18,
$\operatorname {Prob}_\ell (X_t; \mu =0, \lambda =\lambda _0)$
. Note that by Theorem 2.18,
![]() $\operatorname {Prob}_\ell (X_t; \lambda =\lambda _0)=0$
whenever
$\operatorname {Prob}_\ell (X_t; \lambda =\lambda _0)=0$
whenever
![]() $\lambda _0$
is even. Therefore, we assume that
$\lambda _0$
is even. Therefore, we assume that
![]() $\lambda _0=2k-1$
is odd.
$\lambda _0=2k-1$
is odd.
Theorem 4.16. Let
![]() $X_t$
be a bouquet and
$X_t$
be a bouquet and
![]() $k>1$
. Assume that
$k>1$
. Assume that
![]() $\ell $
is odd,
$\ell $
is odd,
![]() $2k-1<\ell $
and
$2k-1<\ell $
and
![]() $k(k-1)<t$
. Then, we have that
$k(k-1)<t$
. Then, we have that
Proof. Note that since
![]() $\ell $
is assumed to be odd and
$\ell $
is assumed to be odd and
![]() $2k-1<\ell $
, it is automatically true that
$2k-1<\ell $
, it is automatically true that
![]() $2k-1<\ell -1$
. Let
$2k-1<\ell -1$
. Let
![]() $\alpha :S\rightarrow \mathbb {Z}_\ell $
be an admissible function for which
$\alpha :S\rightarrow \mathbb {Z}_\ell $
be an admissible function for which
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda <2k-1$
. We set
$\lambda <2k-1$
. We set
![]() $\lambda _0:=2k-1$
, note that by assumption,
$\lambda _0:=2k-1$
, note that by assumption,
![]() $\lambda _0<\ell -1$
. Let
$\lambda _0<\ell -1$
. Let
![]() $\bar {\alpha }=(\bar {\alpha }_1, \dots , \bar {\alpha }_t)$
be the mod-
$\bar {\alpha }=(\bar {\alpha }_1, \dots , \bar {\alpha }_t)$
be the mod-
![]() $\ell $
reduction of
$\ell $
reduction of
![]() $\alpha $
. According to Lemma 4.12,
$\alpha $
. According to Lemma 4.12,
![]() $\bar {\alpha }$
is not a solution to all of the equations
$\bar {\alpha }$
is not a solution to all of the equations
 $$\begin{align*}Q_i(x_1,\dots, x_t)=\sum_{j=1}^{t} x_j^{2i}= 0\end{align*}$$
$$\begin{align*}Q_i(x_1,\dots, x_t)=\sum_{j=1}^{t} x_j^{2i}= 0\end{align*}$$
for
![]() $i<k$
. Then, since
$i<k$
. Then, since
![]() $\lambda _0<\ell -1$
, it follows that
$\lambda _0<\ell -1$
, it follows that
![]() $\beta _n$
is divisible by
$\beta _n$
is divisible by
![]() $\ell $
for
$\ell $
for
![]() $n\leq \lambda _0$
. Let N be the number of nonzero solutions
$n\leq \lambda _0$
. Let N be the number of nonzero solutions
![]() $\bar {\alpha }$
such that
$\bar {\alpha }$
such that
![]() $Q_i(\bar {\alpha })=0$
for all
$Q_i(\bar {\alpha })=0$
for all
![]() $i<k$
. We find that
$i<k$
. We find that
The sum of degrees
![]() $\sum _{i=1}^{k-1} \operatorname {deg} (Q_i)=\sum _{i=1}^{k-1} 2i=k(k-1)$
. Since
$\sum _{i=1}^{k-1} \operatorname {deg} (Q_i)=\sum _{i=1}^{k-1} 2i=k(k-1)$
. Since
![]() $k(k-1)<t$
by assumption, it follows from Theorem 3.1 that
$k(k-1)<t$
by assumption, it follows from Theorem 3.1 that
![]() $N\geq \ell ^{t-k(k-1)}-1$
, and therefore,
$N\geq \ell ^{t-k(k-1)}-1$
, and therefore,
 $$\begin{align*}\operatorname{Prob}_\ell(X_t; \mu=0, \lambda< 2k-1)\leq 1-\frac{\ell^{t-k(k-1)}-1}{\ell^{t}-1}=(1-\ell^{-t})^{-1}(1-\ell^{-k(k-1)}).\end{align*}$$
$$\begin{align*}\operatorname{Prob}_\ell(X_t; \mu=0, \lambda< 2k-1)\leq 1-\frac{\ell^{t-k(k-1)}-1}{\ell^{t}-1}=(1-\ell^{-t})^{-1}(1-\ell^{-k(k-1)}).\end{align*}$$
Example 4.17. Let us now illustrate the above result through an example. Let
![]() $t=10$
and
$t=10$
and
![]() $k=3$
. We study the proportion of admissible vectors for which
$k=3$
. We study the proportion of admissible vectors for which
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda <5$
. Note that
$\lambda <5$
. Note that
![]() $k(k-1)=6<t=10$
. Thus, for all primes
$k(k-1)=6<t=10$
. Thus, for all primes
![]() $\ell>2k-1=7$
, we have that
$\ell>2k-1=7$
, we have that
Next, we study the proportion of admissible vectors
![]() $\alpha =(\alpha _1,\dots , \alpha _t)$
such that
$\alpha =(\alpha _1,\dots , \alpha _t)$
such that
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =1$
. This case is of particular interest, since it is indeed the case when the Iwasawa invariants take on their minimal values.
$\lambda =1$
. This case is of particular interest, since it is indeed the case when the Iwasawa invariants take on their minimal values.
Theorem 4.18. Let
![]() $\ell $
be an odd prime number and
$\ell $
be an odd prime number and
![]() $t \in \mathbb {Z}_{\ge 2}$
. Then, we have that
$t \in \mathbb {Z}_{\ge 2}$
. Then, we have that
 $$\begin{align*}\operatorname{Prob}_{\ell}(X_t;\mu=0, \lambda=1)=\begin{cases} 1-\frac{\ell^{t-1}+(-1)^{\frac{t(\ell-1)}{4}}(\ell-1)\ell^{\frac{t}{2}-1}-1}{\ell^{t}-1},& \text{ if }t \text{ is even}, \\ 1-\frac{\ell^{t-1}-1}{\ell^t-1}, & \text{ if }t\text{ is odd.}\end{cases}\end{align*}$$
$$\begin{align*}\operatorname{Prob}_{\ell}(X_t;\mu=0, \lambda=1)=\begin{cases} 1-\frac{\ell^{t-1}+(-1)^{\frac{t(\ell-1)}{4}}(\ell-1)\ell^{\frac{t}{2}-1}-1}{\ell^{t}-1},& \text{ if }t \text{ is even}, \\ 1-\frac{\ell^{t-1}-1}{\ell^t-1}, & \text{ if }t\text{ is odd.}\end{cases}\end{align*}$$
Proof. Consider the quadratic form
![]() $Q(x_1,\dots , x_t)=\sum _{i=1}^t x_i^2$
defined over
$Q(x_1,\dots , x_t)=\sum _{i=1}^t x_i^2$
defined over
![]() $\mathbb {F}_\ell $
. Then
$\mathbb {F}_\ell $
. Then
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =1$
if and only if
$\lambda =1$
if and only if
![]() $Q(\bar a_1,\ldots ,\bar a_t)\ne 0$
. Therefore,
$Q(\bar a_1,\ldots ,\bar a_t)\ne 0$
. Therefore,
Therefore, the theorem is now a direct consequence of Proposition 3.4.
4.3 Results for small values of t
In this section, we study the distribution of the
![]() $\lambda $
-invariant in greater detail for various values of t, starting with
$\lambda $
-invariant in greater detail for various values of t, starting with
![]() $t=1$
. Throughout, it is assumed that
$t=1$
. Throughout, it is assumed that
![]() $\alpha =(\alpha _1, \dots , \alpha _t)$
is admissible.
$\alpha =(\alpha _1, \dots , \alpha _t)$
is admissible.
 $\mathbf {t=1}$
$\mathbf {t=1}$
The bouquet
![]() $X_1$
consists of a single loop. Let
$X_1$
consists of a single loop. Let
![]() $\ell $
be any prime number (
$\ell $
be any prime number (
![]() $\ell =2$
is allowed). Even though Assumption 2.8 does not hold, we can compute
$\ell =2$
is allowed). Even though Assumption 2.8 does not hold, we can compute
to find that
![]() $\beta _2=\alpha ^2$
. Since
$\beta _2=\alpha ^2$
. Since
![]() $\ell \nmid \alpha $
, we find that
$\ell \nmid \alpha $
, we find that
![]() $\beta _2\in \mathbb {Z}_\ell ^\times $
, and thus,
$\beta _2\in \mathbb {Z}_\ell ^\times $
, and thus,
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =1$
for all choices of
$\lambda =1$
for all choices of
![]() $a\in \mathbb {Z}_\ell ^{\times }$
. In particular, we find for all primes
$a\in \mathbb {Z}_\ell ^{\times }$
. In particular, we find for all primes
![]() $\ell $
,
$\ell $
,
 $$\begin{align*}\operatorname{Prob}_{\ell}(X_1;\mu, \lambda)=\begin{cases} 1,&\text{ if }\mu=0\text{ and }\lambda=1,\\ 0,&\text{ otherwise.} \end{cases}\end{align*}$$
$$\begin{align*}\operatorname{Prob}_{\ell}(X_1;\mu, \lambda)=\begin{cases} 1,&\text{ if }\mu=0\text{ and }\lambda=1,\\ 0,&\text{ otherwise.} \end{cases}\end{align*}$$
The Iwasawa invariants are seen to be
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =1$
for all choices of
$\lambda =1$
for all choices of
![]() $\alpha $
.
$\alpha $
.
 $\mathbf {t=2}$
$\mathbf {t=2}$
Let
![]() $\alpha =(\alpha _1,\alpha _2)\in \mathbb {Z}_\ell ^2$
be an admissible vector. Suppose that
$\alpha =(\alpha _1,\alpha _2)\in \mathbb {Z}_\ell ^2$
be an admissible vector. Suppose that
![]() $\ell \geq 3$
. It follows from Theorems 2.18 and 4.13 that
$\ell \geq 3$
. It follows from Theorems 2.18 and 4.13 that
![]() $\mu =\mu _{\ell }(X_2, \alpha )=0$
and
$\mu =\mu _{\ell }(X_2, \alpha )=0$
and
![]() $\lambda =\lambda _{\ell }(X_2, \alpha )\in \{1,3\}$
. Combined with Theorem 4.18, we deduce the following.
$\lambda =\lambda _{\ell }(X_2, \alpha )\in \{1,3\}$
. Combined with Theorem 4.18, we deduce the following.
Proposition 4.19. Suppose that
![]() $\ell \ge 3$
and
$\ell \ge 3$
and
![]() $t=2$
. Then, we have that
$t=2$
. Then, we have that
![]() $\mu =\mu _{\ell }(X_2, \alpha )=0$
for all choices of
$\mu =\mu _{\ell }(X_2, \alpha )=0$
for all choices of
![]() $\alpha \in \mathbb {Z}_\ell ^2\backslash (\ell \mathbb {Z}_\ell )^2$
. If
$\alpha \in \mathbb {Z}_\ell ^2\backslash (\ell \mathbb {Z}_\ell )^2$
. If
![]() $\ell \equiv 3\bmod {4}$
, then we always have
$\ell \equiv 3\bmod {4}$
, then we always have
![]() $\lambda =1$
. If
$\lambda =1$
. If
![]() $\ell \equiv 1\bmod {4}$
, we have
$\ell \equiv 1\bmod {4}$
, we have
 $$\begin{align*}\operatorname{Prob}_{\ell}(X_2; \mu=0,\lambda=\lambda_0)=\begin{cases} \frac{\ell-1}{\ell+1},&\text{ if }\lambda_0=1,\\ \frac{2}{\ell+1},&\text{ if }\lambda_0=3,\\ 0,&\text{ otherwise.}\\ \end{cases}\end{align*}$$
$$\begin{align*}\operatorname{Prob}_{\ell}(X_2; \mu=0,\lambda=\lambda_0)=\begin{cases} \frac{\ell-1}{\ell+1},&\text{ if }\lambda_0=1,\\ \frac{2}{\ell+1},&\text{ if }\lambda_0=3,\\ 0,&\text{ otherwise.}\\ \end{cases}\end{align*}$$
 $\mathbf {t=3}$
$\mathbf {t=3}$
We now suppose that
![]() $\ell \ge 5$
(the case
$\ell \ge 5$
(the case
![]() $\ell =t=3$
seems a lot more subtle; see Remarks 4.5 and 4.14). As before, Theorem 4.13 tells us that the
$\ell =t=3$
seems a lot more subtle; see Remarks 4.5 and 4.14). As before, Theorem 4.13 tells us that the
![]() $\mu $
-invariant is always zero. We study the distribution of
$\mu $
-invariant is always zero. We study the distribution of
![]() $\lambda $
-invariants in the following proposition.
$\lambda $
-invariants in the following proposition.
Proposition 4.20. Let
![]() $\ell \ge 5$
be a prime number, and let
$\ell \ge 5$
be a prime number, and let
![]() $t=3$
. Then, we have that
$t=3$
. Then, we have that
 $$\begin{align*}\operatorname{Prob}_{\ell}(X_3; \mu=0,\lambda=1)=\frac{\ell^2}{\ell^2+\ell+1}.\end{align*}$$
$$\begin{align*}\operatorname{Prob}_{\ell}(X_3; \mu=0,\lambda=1)=\frac{\ell^2}{\ell^2+\ell+1}.\end{align*}$$
Suppose that
![]() $\ell \equiv 2\bmod {3}$
, then we have that
$\ell \equiv 2\bmod {3}$
, then we have that
 $$\begin{align*}\operatorname{Prob}_{\ell}(X_3; \mu=\mu_0, \lambda=\lambda_0)=\begin{cases} \frac{\ell^2}{\ell^2+\ell+1},&\text{ if }\mu_0=0\text{ and }\lambda_0=1,\\ \frac{\ell+1}{\ell^2+\ell+1},&\text{ if }\mu_0=0\text{ and }\lambda_0=3,\\ 0,&\text{ otherwise.} \end{cases}\end{align*}$$
$$\begin{align*}\operatorname{Prob}_{\ell}(X_3; \mu=\mu_0, \lambda=\lambda_0)=\begin{cases} \frac{\ell^2}{\ell^2+\ell+1},&\text{ if }\mu_0=0\text{ and }\lambda_0=1,\\ \frac{\ell+1}{\ell^2+\ell+1},&\text{ if }\mu_0=0\text{ and }\lambda_0=3,\\ 0,&\text{ otherwise.} \end{cases}\end{align*}$$
Suppose that
![]() $\ell \equiv 1\bmod {3}$
, then we have that
$\ell \equiv 1\bmod {3}$
, then we have that
 $$\begin{align*}\operatorname{Prob}_{\ell}(X_3; \mu=\mu_0, \lambda=\lambda_0)=\begin{cases} \frac{\ell^2}{\ell^2+\ell+1},&\text{ if }\mu_0=0\text{ and }\lambda_0=1,\\ \frac{\ell-7}{\ell^2+\ell+1},&\text{ if }\mu_0=0\text{ and }\lambda_0=3,\\ \frac{8}{\ell^2+\ell+1},&\text{ if }\mu_0=0\text{ and }\lambda_0=5,\\ 0,&\text{ otherwise.} \end{cases}\end{align*}$$
$$\begin{align*}\operatorname{Prob}_{\ell}(X_3; \mu=\mu_0, \lambda=\lambda_0)=\begin{cases} \frac{\ell^2}{\ell^2+\ell+1},&\text{ if }\mu_0=0\text{ and }\lambda_0=1,\\ \frac{\ell-7}{\ell^2+\ell+1},&\text{ if }\mu_0=0\text{ and }\lambda_0=3,\\ \frac{8}{\ell^2+\ell+1},&\text{ if }\mu_0=0\text{ and }\lambda_0=5,\\ 0,&\text{ otherwise.} \end{cases}\end{align*}$$
Proof. Recall from Theorem 4.18 that the probability of
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =1$
is given by
$\lambda =1$
is given by
 $$\begin{align*}\frac{\ell^2}{\ell^2+\ell+1}.\end{align*}$$
$$\begin{align*}\frac{\ell^2}{\ell^2+\ell+1}.\end{align*}$$
Furthermore, Theorems 2.18 and 4.13 imply that
![]() $\lambda \in \{1,3,5\}$
. More specifically, we have
$\lambda \in \{1,3,5\}$
. More specifically, we have
 $$ \begin{align*} \lambda=1&\Leftrightarrow \alpha_1^2+ \alpha_2^2+\alpha_3^2\not\equiv 0\bmod \ell;\\ \lambda=3&\Leftrightarrow \alpha_1^2+\alpha_2^2+ \alpha_3^2\equiv 0\bmod \ell,\quad \alpha_1^4+\alpha_2^4+\alpha_3^4\not\equiv 0\bmod \ell ;\\ \lambda=5&\Leftrightarrow \alpha_1^2+\alpha_2^2+\alpha_3^2\equiv 0\bmod \ell,\quad \alpha_1^4+ \alpha_2^4+ \alpha_3^4\equiv 0\bmod \ell. \end{align*} $$
$$ \begin{align*} \lambda=1&\Leftrightarrow \alpha_1^2+ \alpha_2^2+\alpha_3^2\not\equiv 0\bmod \ell;\\ \lambda=3&\Leftrightarrow \alpha_1^2+\alpha_2^2+ \alpha_3^2\equiv 0\bmod \ell,\quad \alpha_1^4+\alpha_2^4+\alpha_3^4\not\equiv 0\bmod \ell ;\\ \lambda=5&\Leftrightarrow \alpha_1^2+\alpha_2^2+\alpha_3^2\equiv 0\bmod \ell,\quad \alpha_1^4+ \alpha_2^4+ \alpha_3^4\equiv 0\bmod \ell. \end{align*} $$
Suppose that
![]() $\alpha _1^2+\alpha _2^2+\alpha _3^2\equiv 0\bmod \ell $
and that
$\alpha _1^2+\alpha _2^2+\alpha _3^2\equiv 0\bmod \ell $
and that
![]() $\alpha _1^4+\alpha _2^4+\alpha _3^4\equiv 0\bmod \ell $
. By Newton’s identities (see [Reference Mead21]), we can replace the second equation by
$\alpha _1^4+\alpha _2^4+\alpha _3^4\equiv 0\bmod \ell $
. By Newton’s identities (see [Reference Mead21]), we can replace the second equation by
This gives
In particular, we have
![]() $\alpha _1^2\equiv \pm \alpha _2\alpha _3$
and so we are reduced to solving
$\alpha _1^2\equiv \pm \alpha _2\alpha _3$
and so we are reduced to solving
Note that if
![]() $\alpha _3\equiv 0$
, then both
$\alpha _3\equiv 0$
, then both
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
would be divisible by
$\alpha _2$
would be divisible by
![]() $\ell $
, which is not allowed. So, we can divide out by
$\ell $
, which is not allowed. So, we can divide out by
![]() $\alpha _3^{2}$
and we are now reduced to solving
$\alpha _3^{2}$
and we are now reduced to solving
 $$ \begin{align} X^2\pm X+1&\equiv 0\bmod\ell\notag\\ (2X\pm1)^2&\equiv -3\bmod \ell, \end{align} $$
$$ \begin{align} X^2\pm X+1&\equiv 0\bmod\ell\notag\\ (2X\pm1)^2&\equiv -3\bmod \ell, \end{align} $$
where
![]() $X=\alpha _2/\alpha _3$
. In particular, if
$X=\alpha _2/\alpha _3$
. In particular, if
![]() $\left (\frac {-3}{\ell }\right )=-1$
(
$\left (\frac {-3}{\ell }\right )=-1$
(
![]() $\Leftrightarrow \ell \equiv 2\bmod 3$
), (4.5) has no solution. Thus, it is impossible for
$\Leftrightarrow \ell \equiv 2\bmod 3$
), (4.5) has no solution. Thus, it is impossible for
![]() $\lambda $
to be
$\lambda $
to be
![]() $5$
. The probability of
$5$
. The probability of
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =3$
is, therefore,
$\lambda =3$
is, therefore,
 $$\begin{align*}1-\frac{\ell^2}{\ell^2+\ell+1}=\frac{\ell+1}{\ell^2+\ell+1}. \end{align*}$$
$$\begin{align*}1-\frac{\ell^2}{\ell^2+\ell+1}=\frac{\ell+1}{\ell^2+\ell+1}. \end{align*}$$
If
![]() $\left (\frac {-3}{\ell }\right )=+1$
(
$\left (\frac {-3}{\ell }\right )=+1$
(
![]() $\Leftrightarrow \ell \equiv 1\bmod 3$
), then (4.5) admits two solutions. Each choice of X gives rise to
$\Leftrightarrow \ell \equiv 1\bmod 3$
), then (4.5) admits two solutions. Each choice of X gives rise to
![]() $\ell -1$
pairs of
$\ell -1$
pairs of
![]() $(\bar \alpha _2,\bar \alpha _3)\in \mathbb {F}_\ell ^2$
. Taking into account, the two choices of signs, we have in total
$(\bar \alpha _2,\bar \alpha _3)\in \mathbb {F}_\ell ^2$
. Taking into account, the two choices of signs, we have in total
![]() $4(\ell -1)$
choices of
$4(\ell -1)$
choices of
![]() $(\bar \alpha _2,\bar \alpha _3)$
satisfying (4.4). It remains to choose
$(\bar \alpha _2,\bar \alpha _3)$
satisfying (4.4). It remains to choose
![]() $\alpha _1$
such that
$\alpha _1$
such that
Note that
![]() $\pm X$
is a third root of unity, which is always a square in
$\pm X$
is a third root of unity, which is always a square in
![]() $\mathbb {F}_\ell $
(since
$\mathbb {F}_\ell $
(since
![]() $\ell \equiv 1\bmod 6$
, implying that
$\ell \equiv 1\bmod 6$
, implying that
![]() $\mathbb {F}_\ell $
admits a sixth root of unity). Thus, we have two choices of
$\mathbb {F}_\ell $
admits a sixth root of unity). Thus, we have two choices of
![]() $\bar \alpha _1$
for each pair of
$\bar \alpha _1$
for each pair of
![]() $(\bar \alpha _2,\bar \alpha _3)$
. In total, we have
$(\bar \alpha _2,\bar \alpha _3)$
. In total, we have
![]() $8(\ell -1)$
triples of
$8(\ell -1)$
triples of
![]() $(\bar \alpha _1,\bar \alpha _2,\bar \alpha _3)$
satisfying
$(\bar \alpha _1,\bar \alpha _2,\bar \alpha _3)$
satisfying
![]() $\bar \alpha _1^2+\bar \alpha _2^2+\bar \alpha _3^2=\bar \alpha _1^4+\bar \alpha _2^4+\bar \alpha _3^4=0$
. Therefore, the probability
$\bar \alpha _1^2+\bar \alpha _2^2+\bar \alpha _3^2=\bar \alpha _1^4+\bar \alpha _2^4+\bar \alpha _3^4=0$
. Therefore, the probability
![]() $\lambda =5$
is
$\lambda =5$
is
 $$\begin{align*}\frac{8(\ell-1)}{\ell^3-1}=\frac{8}{\ell^2+\ell+1}, \end{align*}$$
$$\begin{align*}\frac{8(\ell-1)}{\ell^3-1}=\frac{8}{\ell^2+\ell+1}, \end{align*}$$
whereas that of
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =3$
is
$\lambda =3$
is
 $$\begin{align*}1-\frac{\ell^2}{\ell^2+\ell+1}-\frac{8}{\ell^2+\ell+1}=\frac{\ell-7}{\ell^2+\ell+1}.\\[-43pt] \end{align*}$$
$$\begin{align*}1-\frac{\ell^2}{\ell^2+\ell+1}-\frac{8}{\ell^2+\ell+1}=\frac{\ell-7}{\ell^2+\ell+1}.\\[-43pt] \end{align*}$$
4.4 Vary t and
 $\alpha $
$\alpha $
In this section, we study question (2) mentioned at the start of the section. In other words, we prove results about the variation of
![]() $\mu _{t,\alpha }=\mu _\ell (X_t,\alpha )$
and
$\mu _{t,\alpha }=\mu _\ell (X_t,\alpha )$
and
![]() $\lambda _{t,\alpha }=\lambda _\ell (X_t,\alpha )$
when both t and
$\lambda _{t,\alpha }=\lambda _\ell (X_t,\alpha )$
when both t and
![]() $\alpha $
vary. Recall that the prime
$\alpha $
vary. Recall that the prime
![]() $\ell $
is fixed. We shall assume that
$\ell $
is fixed. We shall assume that
![]() $\ell $
is odd. Given
$\ell $
is odd. Given
![]() $t\in \mathbb {Z}_{\geq 2}$
, define
$t\in \mathbb {Z}_{\geq 2}$
, define
![]() $\mathcal {T}(\mu ,\lambda ,\ell ,t)$
to be the set of integral vectors
$\mathcal {T}(\mu ,\lambda ,\ell ,t)$
to be the set of integral vectors
![]() $\alpha = (\alpha _1,\ldots ,\alpha _t)\in \mathbb {Z}^t$
such that:
$\alpha = (\alpha _1,\ldots ,\alpha _t)\in \mathbb {Z}^t$
such that:
-
• for some coordinate
 $\alpha _i$
, we have
$\alpha _i$
, we have
 $\ell \nmid \alpha _i$
,
$\ell \nmid \alpha _i$
, -
•
 $\mu _{t,\alpha }=\mu $
and
$\mu _{t,\alpha }=\mu $
and
 $\lambda _{t,\alpha }=\lambda $
.
$\lambda _{t,\alpha }=\lambda $
.
Set
![]() $\mathcal {T}_{\leq x}(\mu ,\lambda ,\ell ,t)$
to be the set of
$\mathcal {T}_{\leq x}(\mu ,\lambda ,\ell ,t)$
to be the set of
![]() $\alpha \in \mathcal {T}(\mu ,\lambda ,\ell ,t)$
such that
$\alpha \in \mathcal {T}(\mu ,\lambda ,\ell ,t)$
such that
![]() $\max \{|\alpha _1|,\ldots , |\alpha _t|\} \leq x$
. Let
$\max \{|\alpha _1|,\ldots , |\alpha _t|\} \leq x$
. Let
![]() $\mathcal {A}_{\leq x}(\ell , t)$
be the set of all tuples
$\mathcal {A}_{\leq x}(\ell , t)$
be the set of all tuples
![]() $\alpha $
such that:
$\alpha $
such that:
-
•
 $\max \{|\alpha _1|,\ldots , |\alpha _t|\}\leq x$
,
$\max \{|\alpha _1|,\ldots , |\alpha _t|\}\leq x$
, -
•
 $\ell \nmid \alpha _i$
for some
$\ell \nmid \alpha _i$
for some
 $1\leq i\leq t$
.
$1\leq i\leq t$
.
On the other hand, fix
![]() $\delta \in (0,1)$
and set
$\delta \in (0,1)$
and set
 $$\begin{align*}\mathcal{T}_{\leq x}(\mu, \lambda, \ell):=\bigcup_{t\leq x^\delta} \mathcal{T}_{\leq x}(\mu, \lambda, \ell,t)\text{ and } \mathcal{A}_{\leq x}(\ell):=\bigcup_{t\leq x^{\delta}} \mathcal{A}_{\leq x}(\ell,t).\end{align*}$$
$$\begin{align*}\mathcal{T}_{\leq x}(\mu, \lambda, \ell):=\bigcup_{t\leq x^\delta} \mathcal{T}_{\leq x}(\mu, \lambda, \ell,t)\text{ and } \mathcal{A}_{\leq x}(\ell):=\bigcup_{t\leq x^{\delta}} \mathcal{A}_{\leq x}(\ell,t).\end{align*}$$
We now state the main result of this section.
Theorem 4.21. With respect to notation above,
 $$\begin{align*}\lim_{x\rightarrow \infty}\frac{\# \mathcal{T}_{\leq x}(0, 1, \ell)}{\# \mathcal{A}_{\leq x}(\ell)}=1-\ell^{-1}. \end{align*}$$
$$\begin{align*}\lim_{x\rightarrow \infty}\frac{\# \mathcal{T}_{\leq x}(0, 1, \ell)}{\# \mathcal{A}_{\leq x}(\ell)}=1-\ell^{-1}. \end{align*}$$
Remark 4.22. We note here that the limit above is equal to the limit of the densities in Theorem 4.18 as
![]() $t\rightarrow \infty $
. This does not follow from formal arguments and further work is required to obtain the result. In fact, it is crucial that the quantity
$t\rightarrow \infty $
. This does not follow from formal arguments and further work is required to obtain the result. In fact, it is crucial that the quantity
![]() $\delta $
defined above lies in the open interval
$\delta $
defined above lies in the open interval
![]() $(0,1)$
. The method used in proving Theorem 4.21 does not extend to
$(0,1)$
. The method used in proving Theorem 4.21 does not extend to
![]() $\delta \geq 1$
.
$\delta \geq 1$
.
Lemma 4.23. With respect to notation above,
for some absolute constant
![]() $c>0$
which is independent of t and x.
$c>0$
which is independent of t and x.
Proof. The number of
![]() $\alpha $
such that
$\alpha $
such that
![]() $\operatorname {max}\left \{|\alpha _1|, |\alpha _2|, \dots , |\alpha _t|\right \}\leq x$
is
$\operatorname {max}\left \{|\alpha _1|, |\alpha _2|, \dots , |\alpha _t|\right \}\leq x$
is
![]() $\left (2\lfloor x\rfloor +1\right )^t$
. The number of tuples such that such that
$\left (2\lfloor x\rfloor +1\right )^t$
. The number of tuples such that such that
![]() $\operatorname {max}\left \{|\alpha _1|, |\alpha _2|, \dots , |\alpha _t|\right \}\leq x$
and
$\operatorname {max}\left \{|\alpha _1|, |\alpha _2|, \dots , |\alpha _t|\right \}\leq x$
and
![]() $\ell $
divides all
$\ell $
divides all
![]() $\alpha _i$
is
$\alpha _i$
is
![]() $\left (2\lfloor x/\ell \rfloor +1\right )^t$
. Therefore, we find that
$\left (2\lfloor x/\ell \rfloor +1\right )^t$
. Therefore, we find that
We have that
 $$ \begin{align*} & \left|\#\mathcal{A}_{\leq x}(\ell, t)-2^t\left(1-\ell^{-t}\right)x^t\right|\\ = & \left| \left(2\lfloor x\rfloor+1\right)^t-\left(2\lfloor x/\ell\rfloor+1\right)^t-2^t\left(1-\ell^{-t}\right)x^t\right|\\ \leq & \left|(2\lfloor x\rfloor+1)^t-(2x)^t\right|+\left|(2\lfloor x/\ell\rfloor+1)^t-(2x/\ell)^t\right|\\ \leq & t\left|(2\lfloor x\rfloor+1)\right|{}^{t-1}+t\left|(2\lfloor x/\ell\rfloor+1)\right|{}^{t-1}<ct x^{t-1}\\ \end{align*} $$
$$ \begin{align*} & \left|\#\mathcal{A}_{\leq x}(\ell, t)-2^t\left(1-\ell^{-t}\right)x^t\right|\\ = & \left| \left(2\lfloor x\rfloor+1\right)^t-\left(2\lfloor x/\ell\rfloor+1\right)^t-2^t\left(1-\ell^{-t}\right)x^t\right|\\ \leq & \left|(2\lfloor x\rfloor+1)^t-(2x)^t\right|+\left|(2\lfloor x/\ell\rfloor+1)^t-(2x/\ell)^t\right|\\ \leq & t\left|(2\lfloor x\rfloor+1)\right|{}^{t-1}+t\left|(2\lfloor x/\ell\rfloor+1)\right|{}^{t-1}<ct x^{t-1}\\ \end{align*} $$
for an absolute constant
![]() $c>0$
. In the above inequalities, we have used the mean value theorem to obtain the bound
$c>0$
. In the above inequalities, we have used the mean value theorem to obtain the bound
and similarly with x replaced by
![]() $x/\ell $
.
$x/\ell $
.
Proposition 4.24. With respect to the notation above, there is an absolute constant
![]() $c>1$
such that
$c>1$
such that
Proof. Note that
 $$\begin{align*}\# \mathcal{A}_{\leq x}(\ell)=\sum_{t=1}^{\lfloor x^\delta\rfloor} \# \mathcal{A}_{\leq x}(\ell,t).\end{align*}$$
$$\begin{align*}\# \mathcal{A}_{\leq x}(\ell)=\sum_{t=1}^{\lfloor x^\delta\rfloor} \# \mathcal{A}_{\leq x}(\ell,t).\end{align*}$$
Therefore, we deduce from Lemma 4.23 that
 $$ \begin{align*} & \left| \# \mathcal{A}_{\leq x}(\ell)-(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}\right|\\ \leq & \left| \# \mathcal{A}_{\leq x}(\ell,\lfloor x^\delta\rfloor ) - (1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}\right|+\sum_{t=1}^{\lfloor x^\delta\rfloor-1} \# \mathcal{A}_{\leq x}(\ell, t)\\ \leq & c\lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+ \sum_{t=1}^{\lfloor x^\delta\rfloor-1}\left( ct x^{t-1} + 2^t(1-\ell^{-t})x^t\right)\\ \leq & c\lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+ (\lfloor x^\delta\rfloor -1)\left( c(\lfloor x^\delta\rfloor -1) x^{\lfloor x^\delta\rfloor-2}\right) + \frac{(2x)\left((2x)^{\lfloor x^\delta\rfloor-1}-1\right)}{2x-1}\\ \leq & c\lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+ c x^{\lfloor x^\delta\rfloor} + 2(2x)^{\lfloor x^\delta\rfloor-1}.\\ \end{align*} $$
$$ \begin{align*} & \left| \# \mathcal{A}_{\leq x}(\ell)-(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}\right|\\ \leq & \left| \# \mathcal{A}_{\leq x}(\ell,\lfloor x^\delta\rfloor ) - (1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}\right|+\sum_{t=1}^{\lfloor x^\delta\rfloor-1} \# \mathcal{A}_{\leq x}(\ell, t)\\ \leq & c\lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+ \sum_{t=1}^{\lfloor x^\delta\rfloor-1}\left( ct x^{t-1} + 2^t(1-\ell^{-t})x^t\right)\\ \leq & c\lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+ (\lfloor x^\delta\rfloor -1)\left( c(\lfloor x^\delta\rfloor -1) x^{\lfloor x^\delta\rfloor-2}\right) + \frac{(2x)\left((2x)^{\lfloor x^\delta\rfloor-1}-1\right)}{2x-1}\\ \leq & c\lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+ c x^{\lfloor x^\delta\rfloor} + 2(2x)^{\lfloor x^\delta\rfloor-1}.\\ \end{align*} $$
After replacing c with a larger absolute constant, we find that each of the three terms in the above sum are
![]() $<\frac {c}{3} (2x)^{\lfloor x^\delta \rfloor -1}$
, and thus, their sum is
$<\frac {c}{3} (2x)^{\lfloor x^\delta \rfloor -1}$
, and thus, their sum is
![]() $<c (2x)^{\lfloor x^\delta \rfloor -1}$
. This proves the result.
$<c (2x)^{\lfloor x^\delta \rfloor -1}$
. This proves the result.
Set
![]() $g(\ell , t)$
to be the number of tuples
$g(\ell , t)$
to be the number of tuples
![]() $\bar {\alpha }=(\bar {\alpha }_1,\dots , \bar {\alpha }_t)\in \mathbb {F}_\ell ^t$
such that:
$\bar {\alpha }=(\bar {\alpha }_1,\dots , \bar {\alpha }_t)\in \mathbb {F}_\ell ^t$
such that:
-
•
 $\bar {\alpha }\neq 0$
,
$\bar {\alpha }\neq 0$
, -
•
 $\sum _i \bar {\alpha }_i^2=0$
.
$\sum _i \bar {\alpha }_i^2=0$
.
Note that by the proof of Theorem 4.18, we have that
 $$ \begin{align}g(\ell, t)=\begin{cases} \ell^{t-1}+(-1)^{\frac{t(\ell-1)}{4}}(\ell-1)\ell^{\frac{t}{2}-1}-1,& \text{ if }t \text{ is even}, \\ \ell^{t-1}-1, & \text{ if }t\text{ is odd.} \end{cases}\end{align} $$
$$ \begin{align}g(\ell, t)=\begin{cases} \ell^{t-1}+(-1)^{\frac{t(\ell-1)}{4}}(\ell-1)\ell^{\frac{t}{2}-1}-1,& \text{ if }t \text{ is even}, \\ \ell^{t-1}-1, & \text{ if }t\text{ is odd.} \end{cases}\end{align} $$
Lemma 4.25. With respect to the notation above,
 $$\begin{align*}\left|\#\mathcal{T}_{\leq x}(0, 1, \ell, t)-\left(1-\frac{g(\ell, t)}{\ell^t-1}\right)(1-\ell^{-t})(2x)^t\right|<2^t\ell tx^{t-1}.\end{align*}$$
$$\begin{align*}\left|\#\mathcal{T}_{\leq x}(0, 1, \ell, t)-\left(1-\frac{g(\ell, t)}{\ell^t-1}\right)(1-\ell^{-t})(2x)^t\right|<2^t\ell tx^{t-1}.\end{align*}$$
Proof. Let
![]() $\mathfrak {U}$
be the set of vectors
$\mathfrak {U}$
be the set of vectors
![]() $\bar {\alpha }\in \mathbb {F}_\ell ^t$
such that:
$\bar {\alpha }\in \mathbb {F}_\ell ^t$
such that:
-
•
 $\bar {\alpha }\neq 0$
,
$\bar {\alpha }\neq 0$
, -
•
 $\sum _i \bar {\alpha }_i^2\neq 0$
.
$\sum _i \bar {\alpha }_i^2\neq 0$
.
Note that
![]() $\#\mathfrak {U}$
is equal to
$\#\mathfrak {U}$
is equal to
![]() $\ell ^t-1-g(\ell , t)$
. Given
$\ell ^t-1-g(\ell , t)$
. Given
![]() $\bar {\alpha }\in \mathfrak {U}$
, set
$\bar {\alpha }\in \mathfrak {U}$
, set
![]() $\mathcal {T}_{\leq x}(\bar {\alpha })$
to denote the subset of
$\mathcal {T}_{\leq x}(\bar {\alpha })$
to denote the subset of
![]() $\mathcal {T}_{\leq x}=\mathcal {T}_{\leq x}(0,1,\ell ,t)$
consisting of tuples
$\mathcal {T}_{\leq x}=\mathcal {T}_{\leq x}(0,1,\ell ,t)$
consisting of tuples
![]() $\alpha $
that reduce to
$\alpha $
that reduce to
![]() $\bar {\alpha }$
modulo-
$\bar {\alpha }$
modulo-
![]() $\ell $
. Let
$\ell $
. Let
![]() $\alpha _i'$
be the integer such that
$\alpha _i'$
be the integer such that
![]() $0\leq \alpha _i'<\ell $
and that
$0\leq \alpha _i'<\ell $
and that
![]() $\alpha _i'$
reduces to
$\alpha _i'$
reduces to
![]() $\bar {\alpha }_i$
. We have
$\bar {\alpha }_i$
. We have
 $$\begin{align*}\# \mathcal{T}_{\leq x}(\bar{\alpha})=\prod_{i=1}^t\left(\lfloor (x-\alpha_i')/\ell\rfloor+ \lfloor (x+\alpha_i')/\ell\rfloor\right).\end{align*}$$
$$\begin{align*}\# \mathcal{T}_{\leq x}(\bar{\alpha})=\prod_{i=1}^t\left(\lfloor (x-\alpha_i')/\ell\rfloor+ \lfloor (x+\alpha_i')/\ell\rfloor\right).\end{align*}$$
It then follows that
 $$\begin{align*}\# \mathcal{T}_{\leq x}(\bar{\alpha})\leq \prod_{i=1}^t\left((x-\alpha_i')/\ell+ (x+\alpha_i')/\ell\right)\leq \left(2x/\ell\right)^t.\end{align*}$$
$$\begin{align*}\# \mathcal{T}_{\leq x}(\bar{\alpha})\leq \prod_{i=1}^t\left((x-\alpha_i')/\ell+ (x+\alpha_i')/\ell\right)\leq \left(2x/\ell\right)^t.\end{align*}$$
Let
![]() $\pi _i:=\{(x-\alpha _i')/\ell \}+\{(x+\alpha _i')/\ell \}$
, we have that
$\pi _i:=\{(x-\alpha _i')/\ell \}+\{(x+\alpha _i')/\ell \}$
, we have that
 $$ \begin{align*}\# \mathcal{T}_{\leq x}(\bar{\alpha})=\prod_{i=1}^{t} \left(2x/\ell-\pi_i\right)\geq (2x/\ell)^t-\left(\sum_{i=1}^t\pi_i\right) (2x/\ell)^{t-1}>(2x/\ell)^t-\left(\frac{2^ttx^{t-1}}{\ell^{t-1}}\right).\end{align*} $$
$$ \begin{align*}\# \mathcal{T}_{\leq x}(\bar{\alpha})=\prod_{i=1}^{t} \left(2x/\ell-\pi_i\right)\geq (2x/\ell)^t-\left(\sum_{i=1}^t\pi_i\right) (2x/\ell)^{t-1}>(2x/\ell)^t-\left(\frac{2^ttx^{t-1}}{\ell^{t-1}}\right).\end{align*} $$
This allows us to deduce that
 $$ \begin{align*}& \left|\#\mathcal{T}_{\leq x}(0, 1, \ell, t)-\left(1-\frac{g(\ell, t)}{\ell^t-1}\right)(1-\ell^{-t})2^t x^t\right|\\=\ & \left|\#\mathcal{T}_{\leq x}(0, 1, \ell, t)-\left(\ell^t-1-g(\ell, t)\right)\left(\frac{2x}{\ell}\right)^t \right|\\=\ & \left| \sum_{\bar{\alpha}\in \mathfrak{U}}\left(\# \mathcal{T}_{\leq x}(\bar{\alpha}) -\left(\frac{2x}{\ell}\right)^t\right) \right|\\\leq\ & \sum_{\bar{\alpha}\in \mathfrak{U}} \left|\# \mathcal{T}_{\leq x}(\bar{\alpha}) -\left(\frac{2x}{\ell}\right)^t\right|\\\leq\ & \left(\ell^t-1-g(\ell,t)\right)\left(\frac{2^ttx^{t-1}}{\ell^{t-1}}\right)\\<\ & 2^t\ell tx^{t-1}.\\[-41pt] \end{align*} $$
$$ \begin{align*}& \left|\#\mathcal{T}_{\leq x}(0, 1, \ell, t)-\left(1-\frac{g(\ell, t)}{\ell^t-1}\right)(1-\ell^{-t})2^t x^t\right|\\=\ & \left|\#\mathcal{T}_{\leq x}(0, 1, \ell, t)-\left(\ell^t-1-g(\ell, t)\right)\left(\frac{2x}{\ell}\right)^t \right|\\=\ & \left| \sum_{\bar{\alpha}\in \mathfrak{U}}\left(\# \mathcal{T}_{\leq x}(\bar{\alpha}) -\left(\frac{2x}{\ell}\right)^t\right) \right|\\\leq\ & \sum_{\bar{\alpha}\in \mathfrak{U}} \left|\# \mathcal{T}_{\leq x}(\bar{\alpha}) -\left(\frac{2x}{\ell}\right)^t\right|\\\leq\ & \left(\ell^t-1-g(\ell,t)\right)\left(\frac{2^ttx^{t-1}}{\ell^{t-1}}\right)\\<\ & 2^t\ell tx^{t-1}.\\[-41pt] \end{align*} $$
Lemma 4.26.
Proof. We have the following estimates:
 $$ \begin{align*} & \left|\#\mathcal{T}_{\leq x}(0, 1, \ell, t)-(1-1/\ell)(1-\ell^{-t})2^t x^t\right|\\\leq\ & \left|\#\mathcal{T}_{\leq x}(0, 1, \ell, t)-\left(1-\frac{g(\ell, t)}{\ell^t-1}\right)(1-\ell^{-t})2^t x^t\right|\\&\ + \left|\left(\frac{\ell^t-1-g(\ell, t)}{\ell^t}\right)2^t x^t-(1-1/\ell)2^t x^t\right|+(1-1/\ell)\ell^{-t}2^tx^t\\<\ & 2^t\ell t x^{t-1}+|\ell^{t-1}-1-g(\ell, t)|(2x/\ell)^t+(2x/\ell)^t\\<\ & 2^t\ell t x^{t-1}+(2x)^t/\ell^{t/2}+(2x/\ell)^t. \end{align*} $$
$$ \begin{align*} & \left|\#\mathcal{T}_{\leq x}(0, 1, \ell, t)-(1-1/\ell)(1-\ell^{-t})2^t x^t\right|\\\leq\ & \left|\#\mathcal{T}_{\leq x}(0, 1, \ell, t)-\left(1-\frac{g(\ell, t)}{\ell^t-1}\right)(1-\ell^{-t})2^t x^t\right|\\&\ + \left|\left(\frac{\ell^t-1-g(\ell, t)}{\ell^t}\right)2^t x^t-(1-1/\ell)2^t x^t\right|+(1-1/\ell)\ell^{-t}2^tx^t\\<\ & 2^t\ell t x^{t-1}+|\ell^{t-1}-1-g(\ell, t)|(2x/\ell)^t+(2x/\ell)^t\\<\ & 2^t\ell t x^{t-1}+(2x)^t/\ell^{t/2}+(2x/\ell)^t. \end{align*} $$
In the above, the second inequality follows from Lemma 4.25, and the third inequality follows from (4.6).
Proposition 4.27. With respect to notation above, we have that
for some absolute constant
![]() $c>0$
.
$c>0$
.
Proof. By Lemma 4.26, we have that
 $$ \begin{align*}& \left|\#\mathcal{T}_{\leq x}(0, 1, \ell)-(1-1/\ell)(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor} \right|\\\leq\ & \left|\#\mathcal{T}_{\leq x}(0, 1, \ell, \lfloor x^\delta\rfloor )-(1-1/\ell)(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}\right|\\&\ +\sum_{t=1}^{\lfloor x^\delta\rfloor-1}\#\mathcal{T}_{\leq x}(0, 1, \ell, t )\\\leq\ & 2^{\lfloor x^\delta\rfloor}\ell \lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+(2x)^{\lfloor x^\delta\rfloor}/\ell^{{\lfloor x^\delta\rfloor}/2}+\left(2x/\ell\right)^{\lfloor x^\delta\rfloor}\\&\ +\sum_{t=1}^{\lfloor x^\delta\rfloor-1}\left((1-1/\ell)2^t x^t+2^t\ell t x^{t-1}+(2x)^t/\ell^{t/2}\right)\\\leq\ & 2^{\lfloor x^\delta\rfloor}\ell \lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+(2x)^{\lfloor x^\delta\rfloor}/\ell^{{\lfloor x^\delta\rfloor}/2}+\left(2x/\ell\right)^{\lfloor x^\delta\rfloor}\\&\ +\sum_{t=1}^{\lfloor x^\delta\rfloor-1}\left(2^t x^t+2^t\ell t x^{t-1}\right)\\\leq\ & 2^{\lfloor x^\delta\rfloor}\ell \lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+(2x)^{\lfloor x^\delta\rfloor}/\ell^{{\lfloor x^\delta\rfloor}/2}+\left(2x/\ell\right)^{\lfloor x^\delta\rfloor}\\&\ +\frac{(2x)^{\lfloor x^\delta\rfloor}-1}{2x-1}+2\ell(\lfloor x^\delta\rfloor-1)^2 (2x)^{{\lfloor x^\delta\rfloor}-2}\\\leq\ & c 2^{\lfloor x^\delta\rfloor}\ell \lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}, \end{align*} $$
$$ \begin{align*}& \left|\#\mathcal{T}_{\leq x}(0, 1, \ell)-(1-1/\ell)(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor} \right|\\\leq\ & \left|\#\mathcal{T}_{\leq x}(0, 1, \ell, \lfloor x^\delta\rfloor )-(1-1/\ell)(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}\right|\\&\ +\sum_{t=1}^{\lfloor x^\delta\rfloor-1}\#\mathcal{T}_{\leq x}(0, 1, \ell, t )\\\leq\ & 2^{\lfloor x^\delta\rfloor}\ell \lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+(2x)^{\lfloor x^\delta\rfloor}/\ell^{{\lfloor x^\delta\rfloor}/2}+\left(2x/\ell\right)^{\lfloor x^\delta\rfloor}\\&\ +\sum_{t=1}^{\lfloor x^\delta\rfloor-1}\left((1-1/\ell)2^t x^t+2^t\ell t x^{t-1}+(2x)^t/\ell^{t/2}\right)\\\leq\ & 2^{\lfloor x^\delta\rfloor}\ell \lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+(2x)^{\lfloor x^\delta\rfloor}/\ell^{{\lfloor x^\delta\rfloor}/2}+\left(2x/\ell\right)^{\lfloor x^\delta\rfloor}\\&\ +\sum_{t=1}^{\lfloor x^\delta\rfloor-1}\left(2^t x^t+2^t\ell t x^{t-1}\right)\\\leq\ & 2^{\lfloor x^\delta\rfloor}\ell \lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}+(2x)^{\lfloor x^\delta\rfloor}/\ell^{{\lfloor x^\delta\rfloor}/2}+\left(2x/\ell\right)^{\lfloor x^\delta\rfloor}\\&\ +\frac{(2x)^{\lfloor x^\delta\rfloor}-1}{2x-1}+2\ell(\lfloor x^\delta\rfloor-1)^2 (2x)^{{\lfloor x^\delta\rfloor}-2}\\\leq\ & c 2^{\lfloor x^\delta\rfloor}\ell \lfloor x^\delta\rfloor x^{\lfloor x^\delta\rfloor-1}, \end{align*} $$
where
![]() $c>0$
is an absolute constant. Note that in the above sum, we used the estimate
$c>0$
is an absolute constant. Note that in the above sum, we used the estimate
 $$ \begin{align*}&\sum_{t=1}^{\lfloor x^\delta\rfloor-1}2^t\ell t x^{t-1}\\\leq\ &\left(\lfloor x^\delta\rfloor-1\right) \operatorname{max}\{2^t\ell t x^{t-1}\mid t=1, \dots, \lfloor x^\delta\rfloor-1\}\\\leq\ &\left(\lfloor x^\delta\rfloor-1\right)\left(2^{\lfloor x^\delta\rfloor-1}\ell (\lfloor x^\delta\rfloor-1) x^{\lfloor x^\delta\rfloor-2}\right).\\[-43pt] \end{align*} $$
$$ \begin{align*}&\sum_{t=1}^{\lfloor x^\delta\rfloor-1}2^t\ell t x^{t-1}\\\leq\ &\left(\lfloor x^\delta\rfloor-1\right) \operatorname{max}\{2^t\ell t x^{t-1}\mid t=1, \dots, \lfloor x^\delta\rfloor-1\}\\\leq\ &\left(\lfloor x^\delta\rfloor-1\right)\left(2^{\lfloor x^\delta\rfloor-1}\ell (\lfloor x^\delta\rfloor-1) x^{\lfloor x^\delta\rfloor-2}\right).\\[-43pt] \end{align*} $$
Proof of Theorem 4.21
It follows from Proposition 4.24 that
 $$\begin{align*}\left| \frac{\# \mathcal{A}_{\leq x}(\ell)}{(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}} - 1\right|< \frac{c(2 x)^{\lfloor x^\delta\rfloor -1}}{(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}}=c(1-\ell^{-\lfloor x^\delta\rfloor})^{-1}(2x)^{-1},\end{align*}$$
$$\begin{align*}\left| \frac{\# \mathcal{A}_{\leq x}(\ell)}{(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}} - 1\right|< \frac{c(2 x)^{\lfloor x^\delta\rfloor -1}}{(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}}=c(1-\ell^{-\lfloor x^\delta\rfloor})^{-1}(2x)^{-1},\end{align*}$$
thus,
 $$ \begin{align}\lim_{x\rightarrow \infty} \left( \frac{\# \mathcal{A}_{\leq x}(\ell)}{(2x)^{\lfloor x^\delta\rfloor}}\right)=1.\end{align} $$
$$ \begin{align}\lim_{x\rightarrow \infty} \left( \frac{\# \mathcal{A}_{\leq x}(\ell)}{(2x)^{\lfloor x^\delta\rfloor}}\right)=1.\end{align} $$
By Proposition 4.27,
 $$ \begin{align*}\left|\frac{\#\mathcal{T}_{\leq x}(0, 1, \ell)}{(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^{\delta}\rfloor}}-(1-1/\ell)\right|&< \frac{c \ell {\lfloor x^\delta\rfloor} (2x)^{{\lfloor x^\delta\rfloor}-1}}{(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}}\\ &= c (1-\ell^{-\lfloor x^\delta\rfloor})^{-1}\ell {\lfloor x^\delta\rfloor} (2x)^{-1}.\end{align*} $$
$$ \begin{align*}\left|\frac{\#\mathcal{T}_{\leq x}(0, 1, \ell)}{(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^{\delta}\rfloor}}-(1-1/\ell)\right|&< \frac{c \ell {\lfloor x^\delta\rfloor} (2x)^{{\lfloor x^\delta\rfloor}-1}}{(1-\ell^{-\lfloor x^\delta\rfloor})(2x)^{\lfloor x^\delta\rfloor}}\\ &= c (1-\ell^{-\lfloor x^\delta\rfloor})^{-1}\ell {\lfloor x^\delta\rfloor} (2x)^{-1}.\end{align*} $$
Recall that
![]() $\delta <1$
, and thus
$\delta <1$
, and thus
![]() ${\lfloor x^\delta \rfloor } (2x)^{-1}$
goes to
${\lfloor x^\delta \rfloor } (2x)^{-1}$
goes to
![]() $0$
as x goes to
$0$
as x goes to
![]() $\infty $
. We thus find that
$\infty $
. We thus find that
 $$\begin{align*}\lim_{x\rightarrow \infty} \left( \frac{\#\mathcal{T}_{\leq x}(0, 1, \ell)}{(2x)^{\lfloor x^{\delta}\rfloor}}\right)=1-\ell^{-1}, \end{align*}$$
$$\begin{align*}\lim_{x\rightarrow \infty} \left( \frac{\#\mathcal{T}_{\leq x}(0, 1, \ell)}{(2x)^{\lfloor x^{\delta}\rfloor}}\right)=1-\ell^{-1}, \end{align*}$$
and the result follows from (4.7).
5 Statistics for multigraphs with two vertices
In this section, we study statistical problems associated with multigraphs consisting of
![]() $2$
vertices
$2$
vertices
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. We study an analog of Question (1) for such graphs. First, let us set up some notation. Let p (resp. q) be the number of undirected loops starting and ending at
$v_2$
. We study an analog of Question (1) for such graphs. First, let us set up some notation. Let p (resp. q) be the number of undirected loops starting and ending at
![]() $v_1$
(resp.
$v_1$
(resp.
![]() $v_2$
). Denote by r the number of undirected edges joining
$v_2$
). Denote by r the number of undirected edges joining
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. The Iwasawa invariants we study significantly depend on the choice of the set S. Let e (resp. g) be the number of directed edges in S starting at
$v_2$
. The Iwasawa invariants we study significantly depend on the choice of the set S. Let e (resp. g) be the number of directed edges in S starting at
![]() $v_1$
(resp.
$v_1$
(resp.
![]() $v_2$
) and ending at
$v_2$
) and ending at
![]() $v_2$
(resp.
$v_2$
(resp.
![]() $v_1$
). Note that
$v_1$
). Note that
![]() $e+g=r$
. We shall assume that
$e+g=r$
. We shall assume that
![]() $r\geq 1$
. If
$r\geq 1$
. If
![]() $e=0$
and
$e=0$
and
![]() $r\geq 1$
, then we replace
$r\geq 1$
, then we replace
![]() $v_1$
with
$v_1$
with
![]() $v_2,$
and thus, without loss of generality, assume that
$v_2,$
and thus, without loss of generality, assume that
![]() $e\geq 1$
. Any graph with
$e\geq 1$
. Any graph with
![]() $2$
-vertices and choice of S corresponds to the
$2$
-vertices and choice of S corresponds to the
![]() $5$
-tuple
$5$
-tuple
![]() $(p,q,r,e,g),$
and let
$(p,q,r,e,g),$
and let
![]() $X_{p,q,r}^{e,g}$
be the associated datum. It conveniences us to express the vector
$X_{p,q,r}^{e,g}$
be the associated datum. It conveniences us to express the vector
![]() $\alpha $
as
$\alpha $
as
![]() $\alpha =(a_1, \dots , a_p, b_1, \dots , b_e, c_1,\dots , c_g, d_1, \dots , d_q)$
, where
$\alpha =(a_1, \dots , a_p, b_1, \dots , b_e, c_1,\dots , c_g, d_1, \dots , d_q)$
, where
![]() $a_i$
is the value of
$a_i$
is the value of
![]() $\alpha $
at the ith loop in S based at
$\alpha $
at the ith loop in S based at
![]() $v_1$
. We set
$v_1$
. We set
![]() $b_i$
to be the value of
$b_i$
to be the value of
![]() $\alpha $
at the ith directed edge in S starting at
$\alpha $
at the ith directed edge in S starting at
![]() $v_1$
and ending at
$v_1$
and ending at
![]() $v_2$
. Denote by
$v_2$
. Denote by
![]() $c_i$
the value of
$c_i$
the value of
![]() $\alpha $
at the ith directed edge in S starting at
$\alpha $
at the ith directed edge in S starting at
![]() $v_2$
and ending at
$v_2$
and ending at
![]() $v_1$
. Finally, let
$v_1$
. Finally, let
![]() $d_i$
be the value of
$d_i$
be the value of
![]() $\alpha $
at the ith loop in S based at
$\alpha $
at the ith loop in S based at
![]() $v_2$
.
$v_2$
.
We write
![]() $\vec {a}$
,
$\vec {a}$
,
![]() $\vec {b}$
,
$\vec {b}$
,
![]() $\vec {c}$
, and
$\vec {c}$
, and
![]() $\vec {d}$
to denote the vectors
$\vec {d}$
to denote the vectors
![]() $(a_1,\dots ,a_p)$
,
$(a_1,\dots ,a_p)$
,
![]() $(b_1, \dots , b_e)$
,
$(b_1, \dots , b_e)$
,
![]() $(c_1, \dots , c_g),$
and
$(c_1, \dots , c_g),$
and
![]() $(d_1, \dots , d_q)$
, respectively. Then,
$(d_1, \dots , d_q)$
, respectively. Then,
![]() $\alpha $
may be represented as a matrix
$\alpha $
may be represented as a matrix
 $$\begin{align*}\alpha= \left( {\begin{array}{cc} {\vec{a}} & {\vec{b}} \\ {\vec{c}} & {\vec{d}} \\ \end{array} } \right), \end{align*}$$
$$\begin{align*}\alpha= \left( {\begin{array}{cc} {\vec{a}} & {\vec{b}} \\ {\vec{c}} & {\vec{d}} \\ \end{array} } \right), \end{align*}$$
where the
![]() $(i, j)$
th entry in this matrix represents the values that
$(i, j)$
th entry in this matrix represents the values that
![]() $\alpha $
takes at the various directed edges that start at
$\alpha $
takes at the various directed edges that start at
![]() $v_i$
and end at
$v_i$
and end at
![]() $v_j$
. Thus, the vectors
$v_j$
. Thus, the vectors
![]() $\vec {a}$
and
$\vec {a}$
and
![]() $\vec {d}$
represent the values taken at loops starting and ending at
$\vec {d}$
represent the values taken at loops starting and ending at
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, respectively.
$v_2$
, respectively.
Recall that Theorem 2.15 gives conditions for Assumption 2.6 to be satisfied. We fix a spanning tree
![]() $\mathfrak {T}$
and assume that
$\mathfrak {T}$
and assume that
![]() $\alpha :S\rightarrow \mathbb {Z}_\ell $
satisfies the conditions of Theorem 2.15. Without loss of generality, assume that
$\alpha :S\rightarrow \mathbb {Z}_\ell $
satisfies the conditions of Theorem 2.15. Without loss of generality, assume that
![]() $\mathfrak {T}$
consists of a single edge joining
$\mathfrak {T}$
consists of a single edge joining
![]() $v_1$
to
$v_1$
to
![]() $v_2$
such that
$v_2$
such that
![]() $S(\mathfrak {T})$
consists of the first directed edge joining
$S(\mathfrak {T})$
consists of the first directed edge joining
![]() $v_1$
to
$v_1$
to
![]() $v_2$
. Then the condition that
$v_2$
. Then the condition that
![]() $\alpha $
is equal to
$\alpha $
is equal to
![]() $0$
on
$0$
on
![]() $S(\mathfrak {T})$
is equivalent to the condition that
$S(\mathfrak {T})$
is equivalent to the condition that
![]() $b_1=0$
. The condition that
$b_1=0$
. The condition that
![]() $\alpha (s)\in \mathbb {Z}_\ell ^\times $
for some
$\alpha (s)\in \mathbb {Z}_\ell ^\times $
for some
![]() $s\in \mathbb {Z}_\ell ^\times $
means that one of the coordinates of
$s\in \mathbb {Z}_\ell ^\times $
means that one of the coordinates of
![]() $\alpha $
is in
$\alpha $
is in
![]() $\mathbb {Z}_\ell ^\times $
. We say that
$\mathbb {Z}_\ell ^\times $
. We say that
![]() $\alpha $
is admissible if these conditions on
$\alpha $
is admissible if these conditions on
![]() $\alpha $
are satisfied. It follows that if
$\alpha $
are satisfied. It follows that if
![]() $\alpha $
is admissible, then Assumption 2.6 is satisfied. Set
$\alpha $
is admissible, then Assumption 2.6 is satisfied. Set
![]() $t:=p+q+r-1$
and given
$t:=p+q+r-1$
and given
![]() $\alpha $
, set
$\alpha $
, set
![]() $\alpha _0\in \mathbb {Z}_\ell ^t$
denote the vector
$\alpha _0\in \mathbb {Z}_\ell ^t$
denote the vector
obtained by dropping the coordinate for
![]() $b_1$
. When
$b_1$
. When
![]() $\alpha $
is admissible, at least one of the coordinates of
$\alpha $
is admissible, at least one of the coordinates of
![]() $\alpha _0$
is not divisible by
$\alpha _0$
is not divisible by
![]() $\ell $
.
$\ell $
.
For example, let
![]() $\ell =5$
, X the multigraph consisting of two vertices
$\ell =5$
, X the multigraph consisting of two vertices
![]() $v_{1}, v_{2}$
, two loops at
$v_{1}, v_{2}$
, two loops at
![]() $v_{1}$
, one loop at
$v_{1}$
, one loop at
![]() $v_{2}$
and two undirected edges between
$v_{2}$
and two undirected edges between
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
, and
$v_{2}$
, and
where
![]() $s_{1}, s_{2}$
are the loops at
$s_{1}, s_{2}$
are the loops at
![]() $v_{1}$
,
$v_{1}$
,
![]() $s_{3}, s_{4}$
are both directed edges going from
$s_{3}, s_{4}$
are both directed edges going from
![]() $v_{1}$
to
$v_{1}$
to
![]() $v_{2}$
, and
$v_{2}$
, and
![]() $s_{5}$
is a loop at
$s_{5}$
is a loop at
![]() $v_{2}$
. Let
$v_{2}$
. Let
![]() $\alpha :S \to \mathbb {Z}_{\ell }$
be defined via
$\alpha :S \to \mathbb {Z}_{\ell }$
be defined via
![]() $s_{1}, s_{2}, s_{5} \mapsto 1$
,
$s_{1}, s_{2}, s_{5} \mapsto 1$
,
![]() $s_{3} \mapsto 0$
, and
$s_{3} \mapsto 0$
, and
![]() $s_{4} \mapsto 2$
, then we get the
$s_{4} \mapsto 2$
, then we get the
![]() $\mathbb {Z}_{5}$
-tower
$\mathbb {Z}_{5}$
-tower

The power series
![]() $f(T)$
starts as follows:
$f(T)$
starts as follows:
Thus,
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda = 3$
. Using SageMath, we calculate
$\lambda = 3$
. Using SageMath, we calculate
We have
for all
![]() $n \ge 1$
.
$n \ge 1$
.
Fixing the choice of S and
![]() $\mathfrak {T}$
, we parameterize the set of admissible vectors by the set of all vectors
$\mathfrak {T}$
, we parameterize the set of admissible vectors by the set of all vectors
![]() $\alpha _0\in \mathbb {Z}_\ell ^t/\left (\ell \mathbb {Z}_\ell \right )^t$
. We denote this set by
$\alpha _0\in \mathbb {Z}_\ell ^t/\left (\ell \mathbb {Z}_\ell \right )^t$
. We denote this set by
![]() $\mathcal {A}(\ell )$
and note that the measure equals
$\mathcal {A}(\ell )$
and note that the measure equals
![]() $\ell ^t-1=(1-\ell ^{-t})\ell ^t$
. Let
$\ell ^t-1=(1-\ell ^{-t})\ell ^t$
. Let
![]() $\mu _{\alpha }$
and
$\mu _{\alpha }$
and
![]() $\lambda _{\alpha }$
be the Iwasawa
$\lambda _{\alpha }$
be the Iwasawa
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
-invariants of
$\lambda $
-invariants of
![]() $X_{p,q,r}^{e,g}$
corresponding to the choice of voltage vector
$X_{p,q,r}^{e,g}$
corresponding to the choice of voltage vector
![]() $\alpha $
. Given constants
$\alpha $
. Given constants
![]() $\mu _0$
and
$\mu _0$
and
![]() $\lambda _0$
, let
$\lambda _0$
, let
![]() $\mathcal {T}(\mu =\mu _0, \lambda =\lambda _0, \ell )$
be the subset of
$\mathcal {T}(\mu =\mu _0, \lambda =\lambda _0, \ell )$
be the subset of
![]() $\mathcal {A}(\ell )$
such that
$\mathcal {A}(\ell )$
such that
![]() $\mu _\alpha =\mu _0$
and
$\mu _\alpha =\mu _0$
and
![]() $\lambda _\alpha =\lambda _0$
. Let
$\lambda _\alpha =\lambda _0$
. Let
![]() $\operatorname {Prob}_\ell (\mu =\mu _0, \lambda =\lambda _0)$
denote the probability that
$\operatorname {Prob}_\ell (\mu =\mu _0, \lambda =\lambda _0)$
denote the probability that
![]() $\mu =\mu _0$
and
$\mu =\mu _0$
and
![]() $\lambda =\lambda _0$
for
$\lambda =\lambda _0$
for
![]() $X_{p,q,r}^{e,g}$
. More precisely, the probability is given by
$X_{p,q,r}^{e,g}$
. More precisely, the probability is given by
where
![]() $\tau $
is the Haar measure on
$\tau $
is the Haar measure on
![]() $\mathbb {Z}_\ell ^t$
as in §4.
$\mathbb {Z}_\ell ^t$
as in §4.
We are able to compute the above probability in the special case
![]() $\mu _0=0$
and
$\mu _0=0$
and
![]() $\lambda _0=1$
. Since the
$\lambda _0=1$
. Since the
![]() $\lambda $
-invariant is odd, these are the minimal values of the Iwasawa invariants. The main result of this section is Theorem 5.3.
$\lambda $
-invariant is odd, these are the minimal values of the Iwasawa invariants. The main result of this section is Theorem 5.3.
Recall that D is the diagonal matrix given by
![]() $D=\operatorname {diag}\left ((2p+r),(2q+r)\right )$
, and write
$D=\operatorname {diag}\left ((2p+r),(2q+r)\right )$
, and write
![]() $M(1+T)=\left (m_{i,j}(T)\right )_{1\leq i, j\leq 2}$
(cf. (2.1)). We are able to explicitly calculate the four values of
$M(1+T)=\left (m_{i,j}(T)\right )_{1\leq i, j\leq 2}$
(cf. (2.1)). We are able to explicitly calculate the four values of
![]() $m_{i,j}(T)$
as follows:
$m_{i,j}(T)$
as follows:
 $$ \begin{align*} m_{1,1}(T)=&\ r+\sum_{i=1}^p \left(2-(1+T)^{a_i}-(1+T)^{-a_i}\right) = r-\sum_{k\geq 2}\sum_{i=1}^p \left({a_i \choose k} +{-a_i\choose k} \right)T^k,\\m_{1,2}(T)= & -\left(1+\sum_{i=2}^{e}(1+T)^{b_i}+\sum_{j=1}^g(1+T)^{-c_j}\right) = -r-\sum_{k\geq 1} \left(\sum_{i=2}^e {b_i \choose k} +\sum_{j=1}^g {-c_j \choose k}\right)T^k,\\m_{2,1}(T)= & -\left(1+\sum_{i=2}^{e}(1+T)^{-b_i}+\sum_{j=1}^g(1+T)^{c_j}\right) = -r-\sum_{k\geq 1} \left(\sum_{i=2}^e {-b_i \choose k} +\sum_{j=1}^g {c_j \choose k}\right)T^k,\\m_{2,2}(T)=&\ r+\sum_{i=1}^q \left(2-(1+T)^{d_i}-(1+T)^{-d_i}\right) = r-\sum_{k\geq 2}\sum_{j=1}^q \left({d_j \choose k} +{-d_j\choose k} \right)T^k. \end{align*} $$
$$ \begin{align*} m_{1,1}(T)=&\ r+\sum_{i=1}^p \left(2-(1+T)^{a_i}-(1+T)^{-a_i}\right) = r-\sum_{k\geq 2}\sum_{i=1}^p \left({a_i \choose k} +{-a_i\choose k} \right)T^k,\\m_{1,2}(T)= & -\left(1+\sum_{i=2}^{e}(1+T)^{b_i}+\sum_{j=1}^g(1+T)^{-c_j}\right) = -r-\sum_{k\geq 1} \left(\sum_{i=2}^e {b_i \choose k} +\sum_{j=1}^g {-c_j \choose k}\right)T^k,\\m_{2,1}(T)= & -\left(1+\sum_{i=2}^{e}(1+T)^{-b_i}+\sum_{j=1}^g(1+T)^{c_j}\right) = -r-\sum_{k\geq 1} \left(\sum_{i=2}^e {-b_i \choose k} +\sum_{j=1}^g {c_j \choose k}\right)T^k,\\m_{2,2}(T)=&\ r+\sum_{i=1}^q \left(2-(1+T)^{d_i}-(1+T)^{-d_i}\right) = r-\sum_{k\geq 2}\sum_{j=1}^q \left({d_j \choose k} +{-d_j\choose k} \right)T^k. \end{align*} $$
We write
![]() $f(T)=\operatorname {det}M(1+T)=\sum _{k=0}^{\infty } \beta _k T^k$
and compute the first few values of
$f(T)=\operatorname {det}M(1+T)=\sum _{k=0}^{\infty } \beta _k T^k$
and compute the first few values of
![]() $\beta _k$
.
$\beta _k$
.
Lemma 5.1. With respect to notation above,
![]() $\beta _n=0$
for
$\beta _n=0$
for
![]() $n\leq 1$
. We find that
$n\leq 1$
. We find that
 $$\begin{align*}\beta_2=\left(\sum_{i=2}^e b_i-\sum_{j=1}^g c_j\right)^2-r\left(\sum_{i=1}^p a_i^2+\sum_{j=2}^e b_j^2+\sum_{k=1}^g c_k^2+\sum_{n=1}^q d_n^2\right).\end{align*}$$
$$\begin{align*}\beta_2=\left(\sum_{i=2}^e b_i-\sum_{j=1}^g c_j\right)^2-r\left(\sum_{i=1}^p a_i^2+\sum_{j=2}^e b_j^2+\sum_{k=1}^g c_k^2+\sum_{n=1}^q d_n^2\right).\end{align*}$$
The Iwasawa
![]() $\lambda $
-invariant satisfies
$\lambda $
-invariant satisfies
![]() $\lambda \geq 1$
, and the following are equivalent:
$\lambda \geq 1$
, and the following are equivalent:
-
1.
 $\mu =0$
and
$\mu =0$
and
 $\lambda =1$
,
$\lambda =1$
, -
2.
 $\ell \nmid \beta _2$
.
$\ell \nmid \beta _2$
.
Proof. In order to compute
![]() $\beta _0$
,
$\beta _0$
,
![]() $\beta _1,$
and
$\beta _1,$
and
![]() $\beta _2$
, we find the matrix
$\beta _2$
, we find the matrix
![]() $M(1+T)$
modulo
$M(1+T)$
modulo
![]() $T^3$
. We find that
$T^3$
. We find that
 $$\begin{align*}M(1+T)= \left( {\begin{array}{cc} {r-\xi_1 T^2} & {-r-\alpha T-\xi_2 T^2} \\ {-r+\alpha T -\xi_3 T^2} & {r-\xi_4T^2} \\ \end{array} } \right)\pmod{T^3}, \end{align*}$$
$$\begin{align*}M(1+T)= \left( {\begin{array}{cc} {r-\xi_1 T^2} & {-r-\alpha T-\xi_2 T^2} \\ {-r+\alpha T -\xi_3 T^2} & {r-\xi_4T^2} \\ \end{array} } \right)\pmod{T^3}, \end{align*}$$
where
 $$ \begin{align*}& \alpha=\sum_{i=2}^e b_i-\sum_{j=1}^g c_j,\\ & \xi_1= \sum_{i=1}^p a_i^2,\\ & \xi_2= \sum_{i=2}^e{b_i\choose 2} +\sum_{j=1}^g {-c_j\choose 2},\\ &\xi_3= \sum_{i=2}^e{-b_i\choose 2} +\sum_{j=1}^g {c_j\choose 2},\\ &\xi_4= \sum_{j=1}^q d_j^2. \end{align*} $$
$$ \begin{align*}& \alpha=\sum_{i=2}^e b_i-\sum_{j=1}^g c_j,\\ & \xi_1= \sum_{i=1}^p a_i^2,\\ & \xi_2= \sum_{i=2}^e{b_i\choose 2} +\sum_{j=1}^g {-c_j\choose 2},\\ &\xi_3= \sum_{i=2}^e{-b_i\choose 2} +\sum_{j=1}^g {c_j\choose 2},\\ &\xi_4= \sum_{j=1}^q d_j^2. \end{align*} $$
Thus,
 $$ \begin{align*}f(T)=& \operatorname{det}M(1+T)\\\equiv & (r-\xi_1 T^2)(r-\xi_4 T^2)-(-r+\alpha T-\xi_2 T^2)(-r-\alpha T-\xi_3 T^2)\\\equiv & \left(\alpha^2-r\sum_{i=1}^4 \xi_i\right)T^2\bmod{T^3}\\\equiv & \left(\left(\sum_{i=2}^e b_i-\sum_{j=1}^g c_j\right)^2-r\left(\sum_{i=1}^p a_i^2+\sum_{j=2}^e b_j^2+\sum_{k=1}^g c_k^2+\sum_{n=1}^q d_n^2\right)\right)T^2\bmod{T^3}.\end{align*} $$
$$ \begin{align*}f(T)=& \operatorname{det}M(1+T)\\\equiv & (r-\xi_1 T^2)(r-\xi_4 T^2)-(-r+\alpha T-\xi_2 T^2)(-r-\alpha T-\xi_3 T^2)\\\equiv & \left(\alpha^2-r\sum_{i=1}^4 \xi_i\right)T^2\bmod{T^3}\\\equiv & \left(\left(\sum_{i=2}^e b_i-\sum_{j=1}^g c_j\right)^2-r\left(\sum_{i=1}^p a_i^2+\sum_{j=2}^e b_j^2+\sum_{k=1}^g c_k^2+\sum_{n=1}^q d_n^2\right)\right)T^2\bmod{T^3}.\end{align*} $$
In other words,
![]() $\beta _0=\beta _1=0$
, and
$\beta _0=\beta _1=0$
, and
 $$\begin{align*}\beta_2=\left(\sum_{i=2}^e b_i-\sum_{j=1}^g c_j\right)^2-r\left(\sum_{i=1}^p a_i^2+\sum_{j=2}^e b_j^2+\sum_{k=1}^g c_k^2+\sum_{n=1}^q d_n^2\right).\\[-51pt] \end{align*}$$
$$\begin{align*}\beta_2=\left(\sum_{i=2}^e b_i-\sum_{j=1}^g c_j\right)^2-r\left(\sum_{i=1}^p a_i^2+\sum_{j=2}^e b_j^2+\sum_{k=1}^g c_k^2+\sum_{n=1}^q d_n^2\right).\\[-51pt] \end{align*}$$
We study the proportion of admissible vectors
![]() $\alpha $
(and thus
$\alpha $
(and thus
![]() $\mathbb {Z}_\ell $
-towers) such that
$\mathbb {Z}_\ell $
-towers) such that
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda =1$
. These are the minimal values of the Iwasawa invariants. We consider the quadratic form over
$\lambda =1$
. These are the minimal values of the Iwasawa invariants. We consider the quadratic form over
![]() $\mathbb {F}_\ell $
in t variables
$\mathbb {F}_\ell $
in t variables
 $$ \begin{align*}& Q_{p, e,g,q}\left(x_1, \dots, x_p, y_2, \dots, y_e, z_1,\dots, z_g, w_1, \dots, w_q\right) \\ := & \left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)^2-r\left(\sum_{i=1}^p x_i^2+\sum_{j=2}^e y_j^2+\sum_{k=1}^g z_k^2+\sum_{n=1}^q w_n^2\right).\end{align*} $$
$$ \begin{align*}& Q_{p, e,g,q}\left(x_1, \dots, x_p, y_2, \dots, y_e, z_1,\dots, z_g, w_1, \dots, w_q\right) \\ := & \left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)^2-r\left(\sum_{i=1}^p x_i^2+\sum_{j=2}^e y_j^2+\sum_{k=1}^g z_k^2+\sum_{n=1}^q w_n^2\right).\end{align*} $$
Note that if
![]() $\ell |r$
, then the quadratic form above is simply given by
$\ell |r$
, then the quadratic form above is simply given by
 $$\begin{align*}Q_{p, e,g,q}\left(x_1, \dots, x_p, y_2, \dots, y_e, z_1,\dots, z_g, w_1, \dots, w_q\right) =\left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)^2,\end{align*}$$
$$\begin{align*}Q_{p, e,g,q}\left(x_1, \dots, x_p, y_2, \dots, y_e, z_1,\dots, z_g, w_1, \dots, w_q\right) =\left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)^2,\end{align*}$$
and is clearly degenerate.
Proposition 5.2. Let
![]() $\ell $
be an odd prime number and
$\ell $
be an odd prime number and
![]() $p,q,r,e,g$
as above. Then, the following assertions hold.
$p,q,r,e,g$
as above. Then, the following assertions hold.
-
1. If
 $\ell |r$
, then
$\ell |r$
, then
 $Q_{p, e,g,q}$
is a degenerate quadratic form over
$Q_{p, e,g,q}$
is a degenerate quadratic form over
 $\mathbb {F}_\ell $
of rank
$\mathbb {F}_\ell $
of rank
 $1$
.
$1$
. -
2. If
 $\ell \nmid r$
, then
$\ell \nmid r$
, then
 $Q_{p, e,g,q}$
is a nondegenerate quadratic form over
$Q_{p, e,g,q}$
is a nondegenerate quadratic form over
 $\mathbb {F}_\ell $
of rank t.
$\mathbb {F}_\ell $
of rank t.
Proof. Let
![]() $Q:=Q_{p,e,g,q}$
, and let
$Q:=Q_{p,e,g,q}$
, and let
![]() $\langle \cdot , \cdot \rangle $
be the associated bilinear form defined by
$\langle \cdot , \cdot \rangle $
be the associated bilinear form defined by
Let
and
We note that
 $$ \begin{align*}& \langle u, u' \rangle= \\ & \left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)\left(\sum_{i=2}^e y_i'-\sum_{j=1}^g z_j'\right)-r\left(\sum_{i=1}^p x_i x_i'+\sum_{j=2}^e y_j y_j'+\sum_{k=1}^g z_k z_k'+\sum_{n=1}^q w_n w_n'\right). \end{align*} $$
$$ \begin{align*}& \langle u, u' \rangle= \\ & \left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)\left(\sum_{i=2}^e y_i'-\sum_{j=1}^g z_j'\right)-r\left(\sum_{i=1}^p x_i x_i'+\sum_{j=2}^e y_j y_j'+\sum_{k=1}^g z_k z_k'+\sum_{n=1}^q w_n w_n'\right). \end{align*} $$
The assertion (1) is clear since the associated pairing is given by
 $$\begin{align*}\langle u, u'\rangle =\left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)\left(\sum_{i=2}^e y_i'-\sum_{j=1}^g z_j'\right).\end{align*}$$
$$\begin{align*}\langle u, u'\rangle =\left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)\left(\sum_{i=2}^e y_i'-\sum_{j=1}^g z_j'\right).\end{align*}$$
Therefore, in order for
![]() $\langle u, \cdot \rangle $
to be identically
$\langle u, \cdot \rangle $
to be identically
![]() $0$
, it is necessary and sufficient for
$0$
, it is necessary and sufficient for
![]() $\sum _{i=2}^e y_i-\sum _{j=1}^g z_j$
to equal
$\sum _{i=2}^e y_i-\sum _{j=1}^g z_j$
to equal
![]() $0$
. The rank is therefore equal to
$0$
. The rank is therefore equal to
![]() $t-(t-1)=1$
.
$t-(t-1)=1$
.
Let us prove part (2), that is, we show that Q is nondegenerate if
![]() $\ell \nmid r$
. Let
$\ell \nmid r$
. Let
![]() $u\neq 0$
be such that
$u\neq 0$
be such that
![]() $\langle u, u' \rangle =0$
for all
$\langle u, u' \rangle =0$
for all
![]() $u'$
. Thus,
$u'$
. Thus,
![]() $x_i$
and
$x_i$
and
![]() $w_n$
are all clearly
$w_n$
are all clearly
![]() $0$
. Consider
$0$
. Consider
![]() $u'$
such that all coordinates are
$u'$
such that all coordinates are
![]() $0$
except for the coordinate
$0$
except for the coordinate
![]() $y_j'$
, which is
$y_j'$
, which is
![]() $1$
. We find that
$1$
. We find that
 $$ \begin{align}\langle u,u' \rangle=\left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)-r y_j=0.\end{align} $$
$$ \begin{align}\langle u,u' \rangle=\left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)-r y_j=0.\end{align} $$
Since
![]() $\ell \nmid r$
, we find that
$\ell \nmid r$
, we find that
![]() $y_j=y_k$
for
$y_j=y_k$
for
![]() $j\neq k$
. Next, consider
$j\neq k$
. Next, consider
![]() $u'$
such that all coordinates are
$u'$
such that all coordinates are
![]() $0$
except for the coordinate
$0$
except for the coordinate
![]() $z_j'$
which is
$z_j'$
which is
![]() $1$
. We find that
$1$
. We find that
 $$ \begin{align}\langle u,u' \rangle=-\left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)-r z_j=0.\end{align} $$
$$ \begin{align}\langle u,u' \rangle=-\left(\sum_{i=2}^e y_i-\sum_{j=1}^g z_j\right)-r z_j=0.\end{align} $$
Setting
![]() $y:=\frac {1}{r}\left (\sum _{i=2}^e y_i-\sum _{j=1}^g z_j\right )$
, it follows from (5.1) and (5.2) that
$y:=\frac {1}{r}\left (\sum _{i=2}^e y_i-\sum _{j=1}^g z_j\right )$
, it follows from (5.1) and (5.2) that
![]() $y_i=y$
,
$y_i=y$
,
![]() $z_j=-y$
for all i and j. We find that
$z_j=-y$
for all i and j. We find that
 $$ \begin{align*}\langle u,u' \rangle&=\left(\sum_{i=2}^e y-\sum_{j=1}^g (-y)\right)\left(\sum_{i=2}^e y_i'-\sum_{j=1}^g z_j'\right)-r\left(\sum_{j=2}^e y y_j' +\sum_{k=1}^g (-y)z_k' \right)\\&=\left((r-1)y-ry\right)\left(\sum_{i=2}^e y_i'-\sum_{j=1}^g z_j'\right)=-y\left(\sum_{i=2}^e y_i'-\sum_{j=1}^g z_j'\right).\end{align*} $$
$$ \begin{align*}\langle u,u' \rangle&=\left(\sum_{i=2}^e y-\sum_{j=1}^g (-y)\right)\left(\sum_{i=2}^e y_i'-\sum_{j=1}^g z_j'\right)-r\left(\sum_{j=2}^e y y_j' +\sum_{k=1}^g (-y)z_k' \right)\\&=\left((r-1)y-ry\right)\left(\sum_{i=2}^e y_i'-\sum_{j=1}^g z_j'\right)=-y\left(\sum_{i=2}^e y_i'-\sum_{j=1}^g z_j'\right).\end{align*} $$
Therefore, it follows that y must be
![]() $0$
in order for the form
$0$
in order for the form
![]() $\langle u, \cdot \rangle $
to be identically
$\langle u, \cdot \rangle $
to be identically
![]() $0$
. Hence, we have shown that
$0$
. Hence, we have shown that
![]() $u=0$
, and thus, Q is nondegenerate.
$u=0$
, and thus, Q is nondegenerate.
Theorem 5.3. Let
![]() $\ell $
be an odd prime and fix
$\ell $
be an odd prime and fix
![]() $(p,q,r,e,g)$
such that
$(p,q,r,e,g)$
such that
![]() $e+g=r$
; set
$e+g=r$
; set
![]() $t:=p+q+r-1$
. Then, the following assertions hold.
$t:=p+q+r-1$
. Then, the following assertions hold.
-
1. Suppose that
 $\ell \mid r$
. Then,
$\ell \mid r$
. Then,  $$\begin{align*}\operatorname{Prob}_\ell\left(\mu=0, \lambda=1\right)=1-(1-\ell^{-t})^{-1}\left(\ell^{-1}-\ell^{-t}\right). \end{align*}$$
$$\begin{align*}\operatorname{Prob}_\ell\left(\mu=0, \lambda=1\right)=1-(1-\ell^{-t})^{-1}\left(\ell^{-1}-\ell^{-t}\right). \end{align*}$$
-
2. Suppose that
 $\ell \nmid r$
. Then, there is a number
$\ell \nmid r$
. Then, there is a number
 $\upsilon \in \{+1, -1\}$
for which
$\upsilon \in \{+1, -1\}$
for which  $$\begin{align*}\operatorname{Prob}_\ell\left(\mu=0, \lambda=1\right)=\begin{cases}1-(1-\ell^{-t})^{-1}\left(\ell^{-1}-\ell^{-t}\right),&\text{ if }t \text{ is odd,}\\ 1-(1-\ell^{-t})^{-1}\left(\ell^{-1}+\upsilon (\ell-1)\ell^{-(t/2+1)}-\ell^{-t}\right),&\text{ if }t \text{ is even.}\\ \end{cases}\end{align*}$$
$$\begin{align*}\operatorname{Prob}_\ell\left(\mu=0, \lambda=1\right)=\begin{cases}1-(1-\ell^{-t})^{-1}\left(\ell^{-1}-\ell^{-t}\right),&\text{ if }t \text{ is odd,}\\ 1-(1-\ell^{-t})^{-1}\left(\ell^{-1}+\upsilon (\ell-1)\ell^{-(t/2+1)}-\ell^{-t}\right),&\text{ if }t \text{ is even.}\\ \end{cases}\end{align*}$$
Proof. First, we prove (1), and thus assume that
![]() $\ell \mid r$
. Let Q be the quadratic form defined in Proposition 5.2. Note that by part (1) of Proposition 5.2, the rank of Q is equal to
$\ell \mid r$
. Let Q be the quadratic form defined in Proposition 5.2. Note that by part (1) of Proposition 5.2, the rank of Q is equal to
![]() $1$
. Let
$1$
. Let
![]() $\bar {\alpha }_0$
be the reduction of
$\bar {\alpha }_0$
be the reduction of
![]() $\alpha _0$
modulo
$\alpha _0$
modulo
![]() $\ell $
. It follows from Lemma 5.1 that
$\ell $
. It follows from Lemma 5.1 that
![]() $\mu _{\alpha }=0$
and
$\mu _{\alpha }=0$
and
![]() $\lambda _\alpha =1$
if and only if
$\lambda _\alpha =1$
if and only if
![]() $Q(\bar {\alpha }_0)\neq 0$
. Therefore, we find that
$Q(\bar {\alpha }_0)\neq 0$
. Therefore, we find that
According to Proposition 3.4,
![]() $N(Q=0)=\ell ^{t-1}$
. Therefore, we find that
$N(Q=0)=\ell ^{t-1}$
. Therefore, we find that
For part (2), it follows from Proposition 5.2(2) that Q is nondegenerate, and thus the rank is t. Setting
![]() $\upsilon $
to denote
$\upsilon $
to denote
![]() $\eta \left ((-1)^{\mathfrak {t}/2}\Delta (Q)\right )$
, it follows from Proposition 3.4 that
$\eta \left ((-1)^{\mathfrak {t}/2}\Delta (Q)\right )$
, it follows from Proposition 3.4 that
 $$\begin{align*}N(Q=0)=\begin{cases} \ell^{t-1}+\upsilon(\ell-1)\ell^{t/2-1},& \text{ if }t\text{ is even,}\\ \ell^{t-1}, & \text{ if }t\text{ is odd.}\end{cases}\end{align*}$$
$$\begin{align*}N(Q=0)=\begin{cases} \ell^{t-1}+\upsilon(\ell-1)\ell^{t/2-1},& \text{ if }t\text{ is even,}\\ \ell^{t-1}, & \text{ if }t\text{ is odd.}\end{cases}\end{align*}$$
Therefore, we find that
 $$\begin{align*}\kern-12pt\operatorname{Prob}_\ell\left(\mu=0, \lambda=1\right)=\begin{cases}1-(1-\ell^{-t})^{-1}\left(\ell^{-1}-\ell^{-t}\right),&\text{ if }t \text{ is odd,}\\ 1-(1-\ell^{-t})^{-1}\left(\ell^{-1}+\upsilon (\ell-1)\ell^{-(t/2+1)}-\ell^{-t}\right),&\text{ if }t \text{ is even.} \end{cases}\\[-41pt]\end{align*}$$
$$\begin{align*}\kern-12pt\operatorname{Prob}_\ell\left(\mu=0, \lambda=1\right)=\begin{cases}1-(1-\ell^{-t})^{-1}\left(\ell^{-1}-\ell^{-t}\right),&\text{ if }t \text{ is odd,}\\ 1-(1-\ell^{-t})^{-1}\left(\ell^{-1}+\upsilon (\ell-1)\ell^{-(t/2+1)}-\ell^{-t}\right),&\text{ if }t \text{ is even.} \end{cases}\\[-41pt]\end{align*}$$
6 Statistics for the Iwasawa invariants of complete graphs
Given an integer
![]() $u\geq 2$
, let
$u\geq 2$
, let
![]() $K_u$
be the complete multigraph with u vertices, that is the multigraph with the set of vertices
$K_u$
be the complete multigraph with u vertices, that is the multigraph with the set of vertices
![]() $V_{K_u} = \{v_1,\ldots , v_u\}$
and with exactly one directed edge
$V_{K_u} = \{v_1,\ldots , v_u\}$
and with exactly one directed edge
![]() $e_{i,j}$
that starts at
$e_{i,j}$
that starts at
![]() $v_i$
and ends at
$v_i$
and ends at
![]() $v_j$
if
$v_j$
if
![]() $i \neq j$
. Furthermore, the graph has no loops. Recall that
$i \neq j$
. Furthermore, the graph has no loops. Recall that
![]() $\pi :E^+_{K_u}\to E_{K_u}$
was the quotient map taking a directed edge to its undirected class. Define
$\pi :E^+_{K_u}\to E_{K_u}$
was the quotient map taking a directed edge to its undirected class. Define
![]() $\gamma :E_{K_u} \to E^+_{K_u}$
to be the section of
$\gamma :E_{K_u} \to E^+_{K_u}$
to be the section of
![]() $\pi $
which sends the unique undirected edge joining
$\pi $
which sends the unique undirected edge joining
![]() $v_i$
to
$v_i$
to
![]() $v_j$
to
$v_j$
to
![]() $e_{i,j}$
if
$e_{i,j}$
if
![]() $i<j$
and to
$i<j$
and to
![]() $e_{j,i}$
if
$e_{j,i}$
if
![]() $j<i$
. Given a function
$j<i$
. Given a function
![]() $\alpha :S \to \mathbb {Z}_\ell $
, let us represent the values taken by
$\alpha :S \to \mathbb {Z}_\ell $
, let us represent the values taken by
![]() $\alpha $
by a matrix
$\alpha $
by a matrix
![]() $(a_{i,j})_{1\leq i,j\leq u}$
with entries defined as follows:
$(a_{i,j})_{1\leq i,j\leq u}$
with entries defined as follows:
 $$\begin{align*}a_{i,j}=\begin{cases} \alpha(e_{i,j}), &\text{ if }i< j,\\ 0, &\text{ if }i\geq j. \end{cases}\end{align*}$$
$$\begin{align*}a_{i,j}=\begin{cases} \alpha(e_{i,j}), &\text{ if }i< j,\\ 0, &\text{ if }i\geq j. \end{cases}\end{align*}$$
In this setting, the matrix
![]() $M(1+T)$
is given by
$M(1+T)$
is given by
![]() $(m_{i,j}(T))_{1 \leq i,j\leq u}$
, where
$(m_{i,j}(T))_{1 \leq i,j\leq u}$
, where
 $$\begin{align*}m_{i,j}(T) = \begin{cases} u-1, & \text{if }i=j, \\ -(1+T)^{a_{i,j}}, & \text{if }i<j, \\ -(1+T)^{-a_{j,i}}, & \text{if }j<i.\end{cases} \end{align*}$$
$$\begin{align*}m_{i,j}(T) = \begin{cases} u-1, & \text{if }i=j, \\ -(1+T)^{a_{i,j}}, & \text{if }i<j, \\ -(1+T)^{-a_{j,i}}, & \text{if }j<i.\end{cases} \end{align*}$$
Recall that the characteristic function
![]() $f(T)$
is the determinant of
$f(T)$
is the determinant of
![]() $M(1+T)$
. We may express
$M(1+T)$
. We may express
![]() $f(T)$
as a power series
$f(T)$
as a power series
![]() $f(T)=\sum _{k=2}^\infty \beta _kT^k$
by Lemma 2.7 and Theorem 2.18. The size of the matrix
$f(T)=\sum _{k=2}^\infty \beta _kT^k$
by Lemma 2.7 and Theorem 2.18. The size of the matrix
![]() $M(1+T)$
increases along with u making its determinant cumbersome to compute. For
$M(1+T)$
increases along with u making its determinant cumbersome to compute. For
![]() $u=4$
and
$u=4$
and
![]() $u=5$
, we can compute explicitly
$u=5$
, we can compute explicitly
 $$ \begin{align*} \beta_2 =& -8\sum_{1\leq i,j \leq 4} a_{i,j}^2-8 \left( a_{1,2} a_{2,3}+ a_{1,2} a_{2,4} + a_{1,3} a_{3,4}+ a_{2,3} a_{3,4}\right) \\ &+8\left( a_{1,2} a_{1,3}+a_{1,2} a_{1,4} + a_{1,3} a_{1,4}+a_{1,3} a_{2,3}+a_{2,4} a_{1,4}+a_{1,4} a_{3,4}+a_{2,4} a_{2,3}+a_{2,4} a_{3,4}\right) \end{align*} $$
$$ \begin{align*} \beta_2 =& -8\sum_{1\leq i,j \leq 4} a_{i,j}^2-8 \left( a_{1,2} a_{2,3}+ a_{1,2} a_{2,4} + a_{1,3} a_{3,4}+ a_{2,3} a_{3,4}\right) \\ &+8\left( a_{1,2} a_{1,3}+a_{1,2} a_{1,4} + a_{1,3} a_{1,4}+a_{1,3} a_{2,3}+a_{2,4} a_{1,4}+a_{1,4} a_{3,4}+a_{2,4} a_{2,3}+a_{2,4} a_{3,4}\right) \end{align*} $$
and
 $$ \begin{align*} \beta_2= &-75 \sum_{1 \leq i,j \leq 5}a_{i,j}^2 - 50 (a_{1,2} a_{2,3} + a_{1,2} a_{2,4}+a_{1,2} a_{2,5}+a_{1,3} a_{3,4}+a_{1,3} a_{3,5}+ a_{1,4} a_{4,5} \\ &+a_{2,3} a_{3,4}+a_{2,3} a_{3,5}+a_{2,4} a_{4,5}+a_{3,4} a_{4,5}) + 50 (a_{1,2} a_{1,3}+a_{1,2} a_{1,4}+ a_{1,2} a_{1,5} +a_{1,3} a_{1,4}\\ &+ a_{1,3} a_{1,5}+ a_{1,3} a_{2,3} +a_{1,4} a_{1,5}+ a_{1,4} a_{2,4}+ a_{1,4} a_{3,4}+ a_{1,5} a_{2,5}+ a_{3,5} a_{1,5} +a_{1,5} a_{4,5}\\ &+ a_{2,3} a_{2,4}+ a_{2,3} a_{2,5} + a_{2,4} a_{2,5}+ a_{2,4} a_{3,4}+ a_{3,5} a_{2,5}+ a_{2,5} a_{4,5} + a_{3,4} a_{3,5}+ a_{3,5} a_{4,5} ), \end{align*} $$
$$ \begin{align*} \beta_2= &-75 \sum_{1 \leq i,j \leq 5}a_{i,j}^2 - 50 (a_{1,2} a_{2,3} + a_{1,2} a_{2,4}+a_{1,2} a_{2,5}+a_{1,3} a_{3,4}+a_{1,3} a_{3,5}+ a_{1,4} a_{4,5} \\ &+a_{2,3} a_{3,4}+a_{2,3} a_{3,5}+a_{2,4} a_{4,5}+a_{3,4} a_{4,5}) + 50 (a_{1,2} a_{1,3}+a_{1,2} a_{1,4}+ a_{1,2} a_{1,5} +a_{1,3} a_{1,4}\\ &+ a_{1,3} a_{1,5}+ a_{1,3} a_{2,3} +a_{1,4} a_{1,5}+ a_{1,4} a_{2,4}+ a_{1,4} a_{3,4}+ a_{1,5} a_{2,5}+ a_{3,5} a_{1,5} +a_{1,5} a_{4,5}\\ &+ a_{2,3} a_{2,4}+ a_{2,3} a_{2,5} + a_{2,4} a_{2,5}+ a_{2,4} a_{3,4}+ a_{3,5} a_{2,5}+ a_{2,5} a_{4,5} + a_{3,4} a_{3,5}+ a_{3,5} a_{4,5} ), \end{align*} $$
respectively. This leads us to introduce the following concept. For integers
![]() $1\le i\leq j\le u$
and
$1\le i\leq j\le u$
and
![]() $1\le k\leq l\le u$
. We say that the tuple
$1\le k\leq l\le u$
. We say that the tuple
![]() $(a_{i,j}, a_{k,l})$
is a linked pair if one of the following three conditions are satisfied:
$(a_{i,j}, a_{k,l})$
is a linked pair if one of the following three conditions are satisfied:
-
•
 $i=k$
and
$i=k$
and
 $i \neq j \neq l$
,
$i \neq j \neq l$
, -
•
 $j=k$
and
$j=k$
and
 $i \neq j \neq l$
,
$i \neq j \neq l$
, -
•
 $j=l$
and
$j=l$
and
 $i \neq j \neq k$
.
$i \neq j \neq k$
.
For example,
![]() $(a_{1,2},a_{2,4})$
,
$(a_{1,2},a_{2,4})$
,
![]() $(a_{1,2},a_{1,4}),$
and
$(a_{1,2},a_{1,4}),$
and
![]() $(a_{1,3},a_{2,3})$
are linked pairs while
$(a_{1,3},a_{2,3})$
are linked pairs while
![]() $(a_{3,4},a_{2,3})$
is not.
$(a_{3,4},a_{2,3})$
is not.
Definition 6.1. Let
![]() $\Pi $
be the following set:
$\Pi $
be the following set:
and let
![]() $\Pi ^c$
be the complement of
$\Pi ^c$
be the complement of
![]() $\Pi $
inside the following set of all linked pairs:
$\Pi $
inside the following set of all linked pairs:
Computations for values of u up to
![]() $7$
suggest that the value of
$7$
suggest that the value of
![]() $\beta _2$
may be given by the following general formula:
$\beta _2$
may be given by the following general formula:
 $$\begin{align*}-(u-2)u^{u-3}\sum_{1\leq i,j\leq u}a_{i,j}^2 + 2u^{u-3}\left( \sum_{\left(a_{i,j}, a_{k,l}\right) \in \Pi^c}a_{i,j}\cdot a_{k,l}-\sum_{\left(a_{i,j}, a_{k,l}\right)\in \Pi}a_{i,j}\cdot a_{k,l}\right). \end{align*}$$
$$\begin{align*}-(u-2)u^{u-3}\sum_{1\leq i,j\leq u}a_{i,j}^2 + 2u^{u-3}\left( \sum_{\left(a_{i,j}, a_{k,l}\right) \in \Pi^c}a_{i,j}\cdot a_{k,l}-\sum_{\left(a_{i,j}, a_{k,l}\right)\in \Pi}a_{i,j}\cdot a_{k,l}\right). \end{align*}$$
In order to write down an explicit formula for the first nonzero coefficient of
![]() $f(T)$
, we will make simplifying assumptions. First, let us suppose the case where all the terms
$f(T)$
, we will make simplifying assumptions. First, let us suppose the case where all the terms
![]() $a_{i,j}$
are zero except for one. This is referred to as a single voltage assignment and we note that computations in this case have been carried out in [Reference Gonet6]. For simplicity, let
$a_{i,j}$
are zero except for one. This is referred to as a single voltage assignment and we note that computations in this case have been carried out in [Reference Gonet6]. For simplicity, let
![]() $a:=a_{12}$
be the nonzero value and assume that
$a:=a_{12}$
be the nonzero value and assume that
![]() $\ell \nmid a$
. Then, the derived multigraphs
$\ell \nmid a$
. Then, the derived multigraphs
![]() $K_u(\mathbb {Z}/\ell ^n \mathbb {Z},S,\alpha _{/n})$
are connected for all n, which follows from Theorem 2.15 by taking
$K_u(\mathbb {Z}/\ell ^n \mathbb {Z},S,\alpha _{/n})$
are connected for all n, which follows from Theorem 2.15 by taking
![]() $\mathfrak {T}$
to be any spanning tree that does not contain an edge joining
$\mathfrak {T}$
to be any spanning tree that does not contain an edge joining
![]() $v_1$
to
$v_1$
to
![]() $v_2$
. Under these assumptions, only the coefficient
$v_2$
. Under these assumptions, only the coefficient
![]() $\beta _2$
will be needed to compute the distribution of the Iwasawa invariants. If one wanted to treat the case of more general voltage assignments, then one would need to compute
$\beta _2$
will be needed to compute the distribution of the Iwasawa invariants. If one wanted to treat the case of more general voltage assignments, then one would need to compute
![]() $\beta _n$
for
$\beta _n$
for
![]() $n\geq 3$
.
$n\geq 3$
.
Lemma 6.2. Let
![]() $\alpha $
be a single voltage assignment described above. The
$\alpha $
be a single voltage assignment described above. The
![]() $\mu $
-invariant of
$\mu $
-invariant of
![]() $f(T)$
is
$f(T)$
is
![]() $\mathrm {ord}_\ell ((u-2)u^{u-3})$
and its
$\mathrm {ord}_\ell ((u-2)u^{u-3})$
and its
![]() $\lambda $
-invariant is
$\lambda $
-invariant is
![]() $1$
.
$1$
.
Proof. By [Reference Gonet6, Th. 5], the determinant of
![]() $M(1+T)$
(defined as in (2.1)) is given by the formula
$M(1+T)$
(defined as in (2.1)) is given by the formula
Since
![]() $(1+T)^{-a}$
is a unit in the Iwasawa algebra, multiplying
$(1+T)^{-a}$
is a unit in the Iwasawa algebra, multiplying
![]() $f(T)$
by
$f(T)$
by
![]() $(1+T)^a$
does not affect its Iwasawa invariants. Thus,
$(1+T)^a$
does not affect its Iwasawa invariants. Thus,
because
![]() $\ell \nmid a$
by assumption. This also shows that
$\ell \nmid a$
by assumption. This also shows that
![]() $\lambda (f(T))=1$
since the
$\lambda (f(T))=1$
since the
![]() $\ell $
-adic valuation of
$\ell $
-adic valuation of
![]() $\beta _2$
is exactly
$\beta _2$
is exactly
![]() $\mathrm {ord}_\ell (-(u-2)u^{u-3})$
and
$\mathrm {ord}_\ell (-(u-2)u^{u-3})$
and
![]() $(1+T)^a -1=Tu(T)$
, where
$(1+T)^a -1=Tu(T)$
, where
![]() $u(T)$
is a unit in the Iwasawa algebra.
$u(T)$
is a unit in the Iwasawa algebra.
There is another special case where the determinant of
![]() $M(1+T)$
can be computed explicitly. Suppose that
$M(1+T)$
can be computed explicitly. Suppose that
![]() $\alpha ^\prime $
is a voltage assignment with
$\alpha ^\prime $
is a voltage assignment with
![]() $a_{1,j}=a$
for all
$a_{1,j}=a$
for all
![]() $2 \leq j \leq u-1$
and zero for all other
$2 \leq j \leq u-1$
and zero for all other
![]() $a_{j,i} (0\leq i\leq j \leq u)$
. The derived multigraphs are again seen to be connected for all n by choosing a suitable spanning tree
$a_{j,i} (0\leq i\leq j \leq u)$
. The derived multigraphs are again seen to be connected for all n by choosing a suitable spanning tree
![]() $\mathfrak {T}$
in Theorem 2.15. One can choose the spanning tree
$\mathfrak {T}$
in Theorem 2.15. One can choose the spanning tree
![]() $\mathfrak {T}$
to pass through all vertices in the following order
$\mathfrak {T}$
to pass through all vertices in the following order
![]() $v_1, v_t, v_{t-1}, \dots , v_2$
. Such a tree must avoid all edges joining
$v_1, v_t, v_{t-1}, \dots , v_2$
. Such a tree must avoid all edges joining
![]() $v_1$
to
$v_1$
to
![]() $v_{j}$
for
$v_{j}$
for
![]() $2\leq j \leq t-1$
.
$2\leq j \leq t-1$
.
Lemma 6.3. Let
![]() $\alpha ^\prime $
be the voltage assignment described above. The
$\alpha ^\prime $
be the voltage assignment described above. The
![]() $\mu $
-invariant of
$\mu $
-invariant of
![]() $f(T)$
is
$f(T)$
is
![]() $\mathrm {ord}_\ell ( (u-2)u^{u-3})$
and its
$\mathrm {ord}_\ell ( (u-2)u^{u-3})$
and its
![]() $\lambda $
-invariant is
$\lambda $
-invariant is
![]() $1$
.
$1$
.
Proof. We set
![]() $\mathfrak {t} := (1+T)^a$
in order to ease notation. With respect to the voltage assignment
$\mathfrak {t} := (1+T)^a$
in order to ease notation. With respect to the voltage assignment
![]() $\alpha '$
, we find that
$\alpha '$
, we find that
![]() $M(1+T)$
is given by
$M(1+T)$
is given by
 $$\begin{align*}M(1+T) = \begin{bmatrix} u-1 & -\mathfrak{t} & -\mathfrak{t} & \cdots & -\mathfrak{t} & -1 \\ -\mathfrak{t}^{-1} & u-1 & -1 & \cdots & -1 & -1 \\ -\mathfrak{t}^{-1} & -1 & u-1 & \cdots & -1 & -1 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ -\mathfrak{t}^{-1} & -1 & -1 & \cdots & u-1 & -1 \\ -1 & -1 & -1 & \cdots & -1 & u-1\end{bmatrix}. \end{align*}$$
$$\begin{align*}M(1+T) = \begin{bmatrix} u-1 & -\mathfrak{t} & -\mathfrak{t} & \cdots & -\mathfrak{t} & -1 \\ -\mathfrak{t}^{-1} & u-1 & -1 & \cdots & -1 & -1 \\ -\mathfrak{t}^{-1} & -1 & u-1 & \cdots & -1 & -1 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ -\mathfrak{t}^{-1} & -1 & -1 & \cdots & u-1 & -1 \\ -1 & -1 & -1 & \cdots & -1 & u-1\end{bmatrix}. \end{align*}$$
Define the two
![]() $1 \times u$
vectors w and v and the
$1 \times u$
vectors w and v and the
![]() $u\times u$
matrix C by
$u\times u$
matrix C by
 $$\begin{align*}w:=\begin{bmatrix} \mathfrak{t} \\ 1 \\ \vdots \\ 1 \end{bmatrix}, v:= \begin{bmatrix} -\mathfrak{t}^{-1} \\ -1 \\ \vdots \\ -1 \end{bmatrix}, C:= \begin{bmatrix} u & 0 & \cdots& 0 & \mathfrak{t}-1 \\ 0 & u & \cdots &0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & u & 0 \\ \mathfrak{t}^{-1}-1 & 0& \cdots & 0 & u \end{bmatrix}. \end{align*}$$
$$\begin{align*}w:=\begin{bmatrix} \mathfrak{t} \\ 1 \\ \vdots \\ 1 \end{bmatrix}, v:= \begin{bmatrix} -\mathfrak{t}^{-1} \\ -1 \\ \vdots \\ -1 \end{bmatrix}, C:= \begin{bmatrix} u & 0 & \cdots& 0 & \mathfrak{t}-1 \\ 0 & u & \cdots &0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & u & 0 \\ \mathfrak{t}^{-1}-1 & 0& \cdots & 0 & u \end{bmatrix}. \end{align*}$$
Then,
![]() $M(1+T) = wv^t + C$
and the matrix determinant lemma gives
$M(1+T) = wv^t + C$
and the matrix determinant lemma gives
![]() $\det M(1+T) = (1+v^tC^{-1}w)\det C$
. To find the inverse of C, we directly compute the minors of C and find
$\det M(1+T) = (1+v^tC^{-1}w)\det C$
. To find the inverse of C, we directly compute the minors of C and find
 $$\begin{align*}C^{-1}= \begin{bmatrix} \frac{-u}{(\mathfrak{t}-1)(\mathfrak{t}^{-1}-1)-u^2} & 0 & \cdots& 0 & \frac{\mathfrak{t}-1}{(\mathfrak{t}-1)(\mathfrak{t}^{-1}-1)-u^2} \\ 0 & \frac{1}{u} & \cdots &0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & \frac{1}{u} & 0 \\ \frac{\mathfrak{t}^{-1}-1}{(\mathfrak{t}-1)(\mathfrak{t}^{-1}-1)-u^2} & 0& \cdots & 0 & \frac{-u}{(\mathfrak{t}-1)(\mathfrak{t}^{-1}-1)-u^2} \end{bmatrix} \end{align*}$$
$$\begin{align*}C^{-1}= \begin{bmatrix} \frac{-u}{(\mathfrak{t}-1)(\mathfrak{t}^{-1}-1)-u^2} & 0 & \cdots& 0 & \frac{\mathfrak{t}-1}{(\mathfrak{t}-1)(\mathfrak{t}^{-1}-1)-u^2} \\ 0 & \frac{1}{u} & \cdots &0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & \frac{1}{u} & 0 \\ \frac{\mathfrak{t}^{-1}-1}{(\mathfrak{t}-1)(\mathfrak{t}^{-1}-1)-u^2} & 0& \cdots & 0 & \frac{-u}{(\mathfrak{t}-1)(\mathfrak{t}^{-1}-1)-u^2} \end{bmatrix} \end{align*}$$
and
![]() $\det\ C = -u^{u-2} \left ( (\mathfrak {t}-1)(\mathfrak {t}^{-1}-1)-u^2 \right )$
. Thus,
$\det\ C = -u^{u-2} \left ( (\mathfrak {t}-1)(\mathfrak {t}^{-1}-1)-u^2 \right )$
. Thus,
From this expression, we see that
![]() $\beta _0=\beta _1=0$
and
$\beta _0=\beta _1=0$
and
 $$\begin{align*}\beta_2 = -(u-2)u^{u-3}\left( \binom{a}{2}+\binom{-a}{2} \right) = -(u-2)u^{u-3}a^2. \end{align*}$$
$$\begin{align*}\beta_2 = -(u-2)u^{u-3}\left( \binom{a}{2}+\binom{-a}{2} \right) = -(u-2)u^{u-3}a^2. \end{align*}$$
Since
![]() $\ell \nmid a$
,
$\ell \nmid a$
,
![]() $f(T) = -(u-2)u^{u-3}T^2 U(T),$
where
$f(T) = -(u-2)u^{u-3}T^2 U(T),$
where
![]() $U(T)$
is a unit. Therefore,
$U(T)$
is a unit. Therefore,
![]() $\mu (f(T)) = \mathrm {ord}_\ell ((u-2)u^{u-3})$
and
$\mu (f(T)) = \mathrm {ord}_\ell ((u-2)u^{u-3})$
and
![]() $\lambda (f(T))=1$
as can be seen from the fact that the
$\lambda (f(T))=1$
as can be seen from the fact that the
![]() $\ell $
-adic valuation of
$\ell $
-adic valuation of
![]() $\beta _2$
is
$\beta _2$
is
![]() $\mu (f(T))$
.
$\mu (f(T))$
.
For example, if we take
![]() $\ell =3$
,
$\ell =3$
,
![]() $X = K_{4}$
and
$X = K_{4}$
and
![]() $\alpha :S \to \mathbb {Z}_{\ell }$
defined via
$\alpha :S \to \mathbb {Z}_{\ell }$
defined via
![]() $s_{1},s_{3}, s_{5}, s_{6} \mapsto 0$
,
$s_{1},s_{3}, s_{5}, s_{6} \mapsto 0$
,
![]() $s_{2} \mapsto 1$
, and
$s_{2} \mapsto 1$
, and
![]() $s_{4} \mapsto 1$
, where
$s_{4} \mapsto 1$
, where
then we get the
![]() $\mathbb {Z}_{3}$
-tower
$\mathbb {Z}_{3}$
-tower

The power series
![]() $f(T)$
starts as follows:
$f(T)$
starts as follows:
Thus,
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda = 1$
as expected by Lemma 6.3. Using SageMath, we calculate
$\lambda = 1$
as expected by Lemma 6.3. Using SageMath, we calculate
and we have
for all
![]() $n \ge 1$
.
$n \ge 1$
.
Fix
![]() $a\in \mathbb {Z}_\ell $
throughout and not divisible by
$a\in \mathbb {Z}_\ell $
throughout and not divisible by
![]() $\ell $
, set
$\ell $
, set
![]() $\alpha (a,u)$
to denote the single voltage assignment with
$\alpha (a,u)$
to denote the single voltage assignment with
![]() $a_{1,2}=a$
and
$a_{1,2}=a$
and
![]() $\alpha ^\prime (a,u)$
to denote the voltage assignment with
$\alpha ^\prime (a,u)$
to denote the voltage assignment with
![]() $a_{1,j}=a$
for
$a_{1,j}=a$
for
![]() $2\leq j \leq u-1$
and zero for the other
$2\leq j \leq u-1$
and zero for the other
![]() $a_{i,j}$
with
$a_{i,j}$
with
![]() $1 \leq i \leq j \leq u$
. Note that
$1 \leq i \leq j \leq u$
. Note that
![]() $\alpha =\alpha (a,u)$
and
$\alpha =\alpha (a,u)$
and
![]() $\alpha ^\prime = \alpha ^\prime (a,u)$
depend on the choice of a and u. We now study the variation of
$\alpha ^\prime = \alpha ^\prime (a,u)$
depend on the choice of a and u. We now study the variation of
![]() $\mu _{u,\alpha }=\mu \left (K_u,\alpha (a,u)\right )$
and
$\mu _{u,\alpha }=\mu \left (K_u,\alpha (a,u)\right )$
and
![]() $\lambda _{u,\alpha }=\lambda \left (K_u,\alpha (a,u)\right )$
in the case where
$\lambda _{u,\alpha }=\lambda \left (K_u,\alpha (a,u)\right )$
in the case where
![]() $a\in \mathbb {Z}_\ell ^\times $
is fixed and u tends to infinity. Let
$a\in \mathbb {Z}_\ell ^\times $
is fixed and u tends to infinity. Let
![]() $\mathcal {T}_{\leq x}(\mu _0,\lambda _0, \alpha ,\ell )$
be the set of nonnegative integers u smaller or equal to x such that
$\mathcal {T}_{\leq x}(\mu _0,\lambda _0, \alpha ,\ell )$
be the set of nonnegative integers u smaller or equal to x such that
![]() $\mu _{u,\alpha }=\mu $
and
$\mu _{u,\alpha }=\mu $
and
![]() $\lambda _{u,\alpha }=\lambda $
. Also define these objects for
$\lambda _{u,\alpha }=\lambda $
. Also define these objects for
![]() $\alpha $
replaced by
$\alpha $
replaced by
![]() $\alpha ^\prime $
. Let
$\alpha ^\prime $
. Let
![]() $\mathcal {A}_{\leq x}$
be the set of nonnegative integers u smaller or equal to x. Note that the dependence on the choice of a is suppressed in our notation.
$\mathcal {A}_{\leq x}$
be the set of nonnegative integers u smaller or equal to x. Note that the dependence on the choice of a is suppressed in our notation.
Theorem 6.4. Let
![]() $a\in \mathbb {Z}_\ell ^\times $
and
$a\in \mathbb {Z}_\ell ^\times $
and
![]() $\gamma \in \{\alpha ,\alpha ^\prime \}$
. Then, we have that
$\gamma \in \{\alpha ,\alpha ^\prime \}$
. Then, we have that
 $$\begin{align*}\lim_{x \to \infty} \frac{\#\mathcal{T}_{\leq x}(\mu,\lambda,\gamma,\ell)}{\#\mathcal{A}_{\leq x}} = \begin{cases}\frac{\ell-2}{\ell}, \quad &\text{if }\mu=0\text{ and }\lambda=1,\\ \frac{\ell-1}{\ell^{\mu+1}}, &\text{if }\mu>0\text{ and }\lambda=1,\\ 0, &\text{if }\lambda \neq 1.\end{cases} \end{align*}$$
$$\begin{align*}\lim_{x \to \infty} \frac{\#\mathcal{T}_{\leq x}(\mu,\lambda,\gamma,\ell)}{\#\mathcal{A}_{\leq x}} = \begin{cases}\frac{\ell-2}{\ell}, \quad &\text{if }\mu=0\text{ and }\lambda=1,\\ \frac{\ell-1}{\ell^{\mu+1}}, &\text{if }\mu>0\text{ and }\lambda=1,\\ 0, &\text{if }\lambda \neq 1.\end{cases} \end{align*}$$
Proof. We set
![]() $\mathcal {T}_{\leq x}(\mu ,\lambda ,\ell )$
to denote
$\mathcal {T}_{\leq x}(\mu ,\lambda ,\ell )$
to denote
![]() $\mathcal {T}_{\leq x}(\mu ,\lambda ,\gamma ,\ell )$
. Lemmas 6.2 and 6.3 assert that
$\mathcal {T}_{\leq x}(\mu ,\lambda ,\gamma ,\ell )$
. Lemmas 6.2 and 6.3 assert that
![]() $\lambda $
is always equal to
$\lambda $
is always equal to
![]() $1$
for both voltage assignments and that
$1$
for both voltage assignments and that
![]() $\mu _{u,\gamma }=\mathrm {ord}_\ell (u-2)+(u-3)\mathrm {ord}_\ell (u)$
. Suppose that
$\mu _{u,\gamma }=\mathrm {ord}_\ell (u-2)+(u-3)\mathrm {ord}_\ell (u)$
. Suppose that
![]() $\mu _{u,\gamma }=\mu>0$
and
$\mu _{u,\gamma }=\mu>0$
and
![]() $\lambda _{u,\gamma }=1$
. Note that this is equivalent to
$\lambda _{u,\gamma }=1$
. Note that this is equivalent to
Choose u large enough so that
![]() $u\geq \mu +2$
. Since
$u\geq \mu +2$
. Since
![]() $\ell \neq 2$
,
$\ell \neq 2$
,
Note that the number of nonnegative integer with
![]() $\ell $
-adic valuation equal to
$\ell $
-adic valuation equal to
![]() $\mu $
smaller or equal to x is greater or equal to
$\mu $
smaller or equal to x is greater or equal to
![]() $\lfloor x/\ell ^{\mu +1} \rfloor (\ell -1)$
. We have the following estimations:
$\lfloor x/\ell ^{\mu +1} \rfloor (\ell -1)$
. We have the following estimations:
 $$ \begin{align*} \#\mathcal{T}_{\leq x}(\mu,1,\ell) &= \#\mathcal{T}_{\leq \mu+1}(\mu,1,\ell)+\#\mathcal{T}_{\mu+2 \leq t \leq x}(\mu,1,\ell)\\&\leq \#\mathcal{T}_{\leq \mu+1}(\mu,1,\ell) + \left( \frac{x}{\ell^{\mu+1}}+1\right)(\ell-1),\\\#\mathcal{T}_{\leq x}(\mu,1,\ell) &\geq \#\mathcal{T}_{\mu+2 \leq t \leq x}(\mu,1,\ell) \geq \left( \frac{x}{\ell^{\mu+1}}-1 \right)(\ell-1)-\left( \frac{\mu+2}{\ell^{\mu+1}}+1\right)(\ell-1), \end{align*} $$
$$ \begin{align*} \#\mathcal{T}_{\leq x}(\mu,1,\ell) &= \#\mathcal{T}_{\leq \mu+1}(\mu,1,\ell)+\#\mathcal{T}_{\mu+2 \leq t \leq x}(\mu,1,\ell)\\&\leq \#\mathcal{T}_{\leq \mu+1}(\mu,1,\ell) + \left( \frac{x}{\ell^{\mu+1}}+1\right)(\ell-1),\\\#\mathcal{T}_{\leq x}(\mu,1,\ell) &\geq \#\mathcal{T}_{\mu+2 \leq t \leq x}(\mu,1,\ell) \geq \left( \frac{x}{\ell^{\mu+1}}-1 \right)(\ell-1)-\left( \frac{\mu+2}{\ell^{\mu+1}}+1\right)(\ell-1), \end{align*} $$
and
![]() $x-1 \leq \#\mathcal {A}_{\leq x}\leq x$
. Therefore,
$x-1 \leq \#\mathcal {A}_{\leq x}\leq x$
. Therefore,
 $$ \begin{align*} \frac{\left( \frac{x}{\ell^{\mu+1}}-1 \right)(\ell-1)-\left( \frac{\mu+2}{\ell^{\mu+1}}+1\right)(\ell-1)}{x} &\leq \frac{\#\mathcal{T}_{\leq x}(\mu,1,\ell)}{\#\mathcal{A}_{\leq x}}\\ &\leq \frac{\#\mathcal{T}_{\leq \mu+1}(\mu,1,\ell) + \left( \frac{x}{\ell^{\mu+1}}+1\right)(\ell-1)}{x-1}. \end{align*} $$
$$ \begin{align*} \frac{\left( \frac{x}{\ell^{\mu+1}}-1 \right)(\ell-1)-\left( \frac{\mu+2}{\ell^{\mu+1}}+1\right)(\ell-1)}{x} &\leq \frac{\#\mathcal{T}_{\leq x}(\mu,1,\ell)}{\#\mathcal{A}_{\leq x}}\\ &\leq \frac{\#\mathcal{T}_{\leq \mu+1}(\mu,1,\ell) + \left( \frac{x}{\ell^{\mu+1}}+1\right)(\ell-1)}{x-1}. \end{align*} $$
Letting
![]() $x \to \infty $
, the result follows.
$x \to \infty $
, the result follows.
For the case
![]() $\mu _{u,\gamma }=0$
and
$\mu _{u,\gamma }=0$
and
![]() $\lambda _{u,\gamma }=1$
, we need both
$\lambda _{u,\gamma }=1$
, we need both
![]() $\mathrm {ord}_\ell (u-2)$
and
$\mathrm {ord}_\ell (u-2)$
and
![]() $\mathrm {ord}_\ell (u)$
to be zero. We find
$\mathrm {ord}_\ell (u)$
to be zero. We find
 $$\begin{align*}\frac{\left( \frac{x}{\ell}-1\right)(\ell-2)}{x} \leq \frac{\#\mathcal{T}_{\leq x}(\mu,1,\ell)}{\#\mathcal{A}_{\leq x}} \leq \frac{\left( \frac{x}{\ell}+1\right)(\ell-2)}{x-1}. \end{align*}$$
$$\begin{align*}\frac{\left( \frac{x}{\ell}-1\right)(\ell-2)}{x} \leq \frac{\#\mathcal{T}_{\leq x}(\mu,1,\ell)}{\#\mathcal{A}_{\leq x}} \leq \frac{\left( \frac{x}{\ell}+1\right)(\ell-2)}{x-1}. \end{align*}$$
We get the stated proportion of the theorem by letting x goes to infinity.
Remark 6.5. The sum of densities in the statement of Theorem 6.4 for all values of
![]() $(\mu ,\lambda )$
is equal to
$(\mu ,\lambda )$
is equal to
![]() $1-1/\ell $
and not
$1-1/\ell $
and not
![]() $1$
. This is indeed possible for a sequence of numbers. For instance, consider the sequence
$1$
. This is indeed possible for a sequence of numbers. For instance, consider the sequence
![]() $g_i=i$
. Then for any value of
$g_i=i$
. Then for any value of
![]() $j>0$
, the density of values i for which
$j>0$
, the density of values i for which
![]() $g_i=j$
is equal to
$g_i=j$
is equal to
![]() $0$
, and thus, the sum of densities over all values of j is
$0$
, and thus, the sum of densities over all values of j is
![]() $0$
, not
$0$
, not
![]() $1$
.
$1$
.
Remark 6.6. All the
![]() $\mathbb {Z}_{\ell }$
-towers over complete graphs studied in this section have
$\mathbb {Z}_{\ell }$
-towers over complete graphs studied in this section have
![]() $\lambda = 1$
, but we note in passing that there are examples where
$\lambda = 1$
, but we note in passing that there are examples where
![]() $\lambda \neq 1$
. For example, if we take
$\lambda \neq 1$
. For example, if we take
![]() $\ell =3$
,
$\ell =3$
,
![]() $X = K_{4}$
and
$X = K_{4}$
and
![]() $\alpha :S \to \mathbb {Z}_{\ell }$
defined via
$\alpha :S \to \mathbb {Z}_{\ell }$
defined via
![]() $s_{4}, s_{5}, s_{6} \mapsto 0$
,
$s_{4}, s_{5}, s_{6} \mapsto 0$
,
![]() $s_{1} \mapsto 1$
,
$s_{1} \mapsto 1$
,
![]() $s_{2} \mapsto 2$
, and
$s_{2} \mapsto 2$
, and
![]() $s_{3} \mapsto 4$
, where
$s_{3} \mapsto 4$
, where
then we get the
![]() $\mathbb {Z}_{3}$
-tower
$\mathbb {Z}_{3}$
-tower

The power series
![]() $f(T)$
starts as follows:
$f(T)$
starts as follows:
Thus,
![]() $\mu =0$
and
$\mu =0$
and
![]() $\lambda = 5$
. Using SageMath, we calculate
$\lambda = 5$
. Using SageMath, we calculate
We have
for all
![]() $n \ge 1$
.
$n \ge 1$
.
Acknowledgments
D.V. would like to thank Kevin McGown for several stimulating discussions. We thank the anonymous referee for valuable comments and suggestions.