Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T19:44:47.777Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Discrete Subgroups and Homogeneous Spaces of Nilpotent Lie Groups

Published online by Cambridge University Press:  22 January 2016

Yozô Matsushima
Yozô Matsushima*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

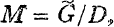Recently A, Malcev has shown that the homogeneous space of a connected nilpotent Lie group G is the direct product of a compact space and an Euclidean-space and that the compact space of this direct decomposition is also a homogeneous space of a connected subgroup of G. Any compact homogeneous space M of a connected nilpotent Lie group is of the form where 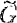is a connected simply connected nilpotent group whose structure constants are rational numbers in a suitable coordinate system and D is a discrete subgroup of G.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 2 , February 1951 , pp. 95 - 110
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1951

References

[1] Chevalley, C., On the topological structure of solvable groups, Ann, of Math. 42 (1941).Google Scholar
[2] Chevalley, C., and Eilenberg, S., Cohomology theory of Lie groups and Lie algebras, Trans. of Amer. Math. Soc. 63 (1948).Google Scholar
[3] Eilenberg, S. and MacLane, S., Relations between homology and homotopy groups of spaces, Ann. of Math. 46 (1945).CrossRefGoogle Scholar
[4] Eilenberg, S. and MacLane, S., Cohomology theory in abstract groups. I, Ann. of Math. 48 (1947).Google Scholar
[5] Hopf, H., fundamental Gruppe und zweite Bettische Gruppe, Comment. Math. Helv. 14 (1942).Google Scholar
[6] Hopf, H., Ueber die Bettische Gruppen, die zu einer beliebigen Gruppe gehoren, Commet. Math. Helv. 17 (1945).Google Scholar
[7] Kuranishi, M., On everywhere dense imbedding of free groups in Lie groups, Nagoya Math. J., this volume.Google Scholar
[8] Malcev, A., On a class of homogeneous spaces, Izvestiya Akad. Nauk SSSR. Ser. Math. 13 (1949) (in Russian).Google Scholar