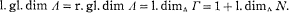Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Eilenberg, Samuel
Rosenberg, Alex
and
Zelinsky, Daniel
1957.
On the Dimension of Modules and Algebras, VIII. Dimension of Tensor Products.
Nagoya Mathematical Journal,
Vol. 12,
Issue. ,
p.
71.
Eilenberg, Samuel
and
Nakayama, Tadasi
1957.
On the Dimension of Modules and Algebras, V. Dimension of Residue Rings.
Nagoya Mathematical Journal,
Vol. 11,
Issue. ,
p.
9.
Jans, J. P.
and
Nakayama, Tadasi
1957.
On the Dimension of Modules and Algebras, VII. Algebras with Finite-Dimensional Residue-Algebras.
Nagoya Mathematical Journal,
Vol. 11,
Issue. ,
p.
67.
Chase, Stephen U.
1961.
A Generalization of the Ring of Triangular Matrices.
Nagoya Mathematical Journal,
Vol. 18,
Issue. ,
p.
13.
Harada, Manabu
1966.
Hereditary Semi-Primary Rings and Tri-Angular Matrix Rings.
Nagoya Mathematical Journal,
Vol. 27,
Issue. 2,
p.
463.
Zaks, Abraham
1967.
Residue Rings of Semi-Primary Hereditary Rings*.
Nagoya Mathematical Journal,
Vol. 30,
Issue. ,
p.
279.
Zaks, A.
1968.
Semi-primary hereditary rings.
Israel Journal of Mathematics,
Vol. 6,
Issue. 4,
p.
359.
Zaks, Abraham
1968.
Semiprimary rings of generalized triangular type.
Journal of Algebra,
Vol. 9,
Issue. 1,
p.
54.
Zaks, Abraham
1969.
Injective dimension of semi-primary rings.
Journal of Algebra,
Vol. 13,
Issue. 1,
p.
73.
Eisenbud, David
and
Robson, J.C
1970.
Hereditary Noetherian prime rings.
Journal of Algebra,
Vol. 16,
Issue. 1,
p.
86.
Helzer, Garry
1971.
The skeleton of a perfect ring.
Journal of Algebra,
Vol. 17,
Issue. 4,
p.
451.
Năstăsescu, Constantin
1971.
Quelques remarques sur la dimension homologique des anneaux. Eléments réguliers.
Journal of Algebra,
Vol. 19,
Issue. 4,
p.
470.
Wehlen, Joseph A.
1971.
Algebras of Finite Cohomological Dimension.
Nagoya Mathematical Journal,
Vol. 43,
Issue. ,
p.
127.
Wehlen, Joseph A.
1973.
Triangular matrix algebras over Hensel rings.
Proceedings of the American Mathematical Society,
Vol. 37,
Issue. 1,
p.
69.
Osofsky, Barbara L.
1974.
The subscript of ℵ_{𝑛} ,projective dimension, and the vanishing of lim_{←}⁽ⁿ⁾.
Bulletin of the American Mathematical Society,
Vol. 80,
Issue. 1,
p.
8.
1976.
Algebra, Topology, and Category Theory.
p.
221.
Green, Edward L.
and
Reiten, Idun
1976.
On the construction of ring extensions.
Glasgow Mathematical Journal,
Vol. 17,
Issue. 1,
p.
1.
Kirkman, Ellen
and
Kuzmanovich, James
1987.
Matrix subrings having finite global dimension.
Journal of Algebra,
Vol. 109,
Issue. 1,
p.
74.
Stafford, J. T.
1987.
Séminaire d'Algèbre Paul Dubreil et Marie-Paule Malliavin.
Vol. 1296,
Issue. ,
p.
247.
Kirkman, Ellen
and
Kuzmanovich, James
1988.
On the global dimension of a ring modulo its nilpotent radical.
Proceedings of the American Mathematical Society,
Vol. 102,
Issue. 1,
p.
25.