Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1989.
Scattering Theory for Hyperbolic Operators.
Vol. 21,
Issue. ,
p.
355.
Stefanov, P. D.
1990.
Inverse Methods in Action.
p.
212.
Stefanov, Plamen D.
1991.
Inverse scattering problem for moving obstacles.
Mathematische Zeitschrift,
Vol. 207,
Issue. 1,
p.
461.


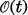 has been studied by Cooper [1] and Cooper and Strauss [2] etc. In their works it has been assumed that the obstacle
has been studied by Cooper [1] and Cooper and Strauss [2] etc. In their works it has been assumed that the obstacle 