Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sirao, Tunekiti
and
Watanabe, Hisao
1968.
On the Hölder continuity of stationary Gaussian processes.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 44,
Issue. 6,
SEGUCHI, Tsunetami
1969.
SHIFT-COMMUTATIVE LINEAR OPERATORS AND STATIONARY PROCESSES.
Memoirs of the Faculty of Science, Kyushu University. Series A, Mathematics,
Vol. 23,
Issue. 2,
p.
106.
Kawada, Takayuki
1969.
On the Upper and Lower Class For Gaussian Processes with Several Parameters.
Nagoya Mathematical Journal,
Vol. 35,
Issue. ,
p.
109.
Sirao, Tunekiti
and
Watanabe, Hisao
1970.
On the upper and lower class for stationary Gaussian processes.
Transactions of the American Mathematical Society,
Vol. 147,
Issue. 2,
p.
301.
Pitt, Loren D.
1971.
A Markov property for Gaussian processes with a multidimensional parameter.
Archive for Rational Mechanics and Analysis,
Vol. 43,
Issue. 5,
p.
367.
Katkauskaitė, A.
1974.
Asymptotic behavior of stable random fields.
Lithuanian Mathematical Transactions,
Vol. 14,
Issue. 2,
p.
214.
Weber, Michel
1977.
Séminaire de Probabilités XI.
Vol. 581,
Issue. ,
p.
196.
Ortega, Joaquin
1982.
Asymptotic behaviour of Gaussian random fields.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 59,
Issue. 2,
p.
169.
Weber, M.
1983.
Ecole d’Eté de Probabilités de Saint-Flour XI — 1981.
Vol. 976,
Issue. ,
p.
383.
Sen, Pradip Kumar
and
Wichura, Michael J
1984.
Estimation of first crossing time distribution for N-parameter Brownian motion processes relative to upper class boundaries.
Journal of Multivariate Analysis,
Vol. 15,
Issue. 2,
p.
201.
Weber, Michel
1989.
The supremum of Gaussian processes with a constant variance.
Probability Theory and Related Fields,
Vol. 81,
Issue. 4,
p.
585.
Garet, Olivier
2000.
Asymptotic behaviour of Gaussian processes with integral representation.
Stochastic Processes and their Applications,
Vol. 89,
Issue. 2,
p.
287.
CsõRGõ, MiklÓS
2002.
A glimpse of the impact of pál erd#ous on probability and statistics.
Canadian Journal of Statistics,
Vol. 30,
Issue. 4,
p.
493.
Dudley, R. M.
2010.
Selected Works of R.M. Dudley.
p.
187.


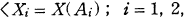
 is subject to an
is subject to an 