Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-16T17:11:09.599Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Complement of Levi-Flats in Kähler Manifolds of Dimension ≥ 3

Published online by Cambridge University Press:  11 January 2016

Takeo Ohsawa
Takeo Ohsawa*
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku Furo-cho 464-8602, Nagoya, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

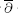Applying the L2 method of solving the -equation, it is shown that compact Kähler manifolds of dimension ≥ 3 admit no Levi flat real analytic hypersurfaces whose complements are Stein.

Keywords

32V4053C40
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 185 , 2007 , pp. 161 - 169
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2007

References

[A] Aronszajn, N., A unique continuation theorem for solutions of elliptic partial differential equations or inequalities of second order, J. Math. Pures Appl., 36 (1957), 235–249.Google Scholar
[C-S-W] Cao, J., Shaw, M.-C., and Wang, L., Estimates for the -Neumann problem and nonexistence of C2 Levi-flat hypersurfaces in ℂℚ n , Math. Z., 248 (2004), 183–221; Erratum, 223–225.CrossRefGoogle Scholar
[D] Demailly, J.-P., Cohomology of q-convex spaces in top degree, Math. Z., 204 (1990), 283–295.CrossRefGoogle Scholar
[D-O] Diederich, K., and Ohsawa, T., Harmonic mappings and the disc bundles over compact Kähler manifolds, Publ. RIMS, 21 (1985), 819–833.CrossRefGoogle Scholar
[G] Grauert, H., Bemerkenswerte pseudokonvexe Mannigfaltigkeiten, Math. Z., 81 (1963), 377-392CrossRefGoogle Scholar
[H-1] Hörmander, L., L2 estimates and existence theorems for the -operator, Acta Math, 113 (1965), 89–152.CrossRefGoogle Scholar
[H-2] Hörmander, L., An Introduction to Complex Analysis in Several Variavbles, 2004, North Holland Publishing Company, 1973.Google Scholar
[I] Iordan, A., On the existence of smooth Levi-flat hypersurfaces in ℂℚn, Advanced Studies in Pure Mathematics 42, Complex Analysis in Several Variables, pp. 123–126.Google Scholar
[M] Mok, N., The Serre problem on Riemann surfaces, Math. Ann., 258 (1981), 145–168.CrossRefGoogle Scholar
[Ne] Nemirovski, S., Stein domains with Levi-flat boundaries on compact complex surfaces, Math. Notes, 66, no.4 (1999), 522–525.CrossRefGoogle Scholar
[O-1] Ohsawa, T., A reduction theorem for cohomology groups of very strongly q convex Kähler manifolds, Invent. Math. 63 (1981), 335–354. Addendum: Invent. Math., 66 (1982), 391–393.CrossRefGoogle Scholar
[O-2] Ohsawa, T., A Stein domain with smooth boundary which has a product structure, Publ. RIMS, 18 (1982), 1185-1186.CrossRefGoogle Scholar
[O-3] Ohsawa, T., On the Levi-flats in complex tori of dimension two, Publ. RIMS, 42 (2006), 361–377. Supplement; 379–382, Erratum; preprint.CrossRefGoogle Scholar
[O-4] Ohsawa, T., A Levi-flat in a Kummer surface whose complement is strongly pseudoconvex, Osaka J. Math., 43 (2006), 747–750 Google Scholar
[O-T] Ohsawa, T., and Takegoshi, K., Hodge spectral sequence on pseudoconvex domains, Math. Z., 197 (1988), 1–12.CrossRefGoogle Scholar
[S-1] Siu, Y.T., Nonexistence of smooth Levi-flat hypersurfaces in complex projective spaces of dimension ≥ 3, Ann. of Math., 151 (2000), 1217-1243.CrossRefGoogle Scholar
[S-2] Siu, Y.T., -regularity for weakly pseudoconvex domains in compact Hermitian spaces with respect to invariant metrics, Ann. of Math., 156 (2002), 595–621.CrossRefGoogle Scholar