Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T23:38:47.787Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Cohen-Macaulayfication of certain Buchsbaum rings

Published online by Cambridge University Press:  22 January 2016

Shiro Goto
Shiro Goto*
Affiliation:
Department of Mathematics, Nihon University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

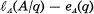Let A be a Noetherian local ring of dimension d and with maximal ideal m. Then A is called Buchsbaum if every system of parameters is a weak sequence. This is equivalent to the condition that, for every parameter ideal q, the difference is an invariant I(A) of A not depending on the choice of q. (See Section 2 for the detail.) The concept of Buchsbaum rings was introduced by Stückrad and Vogel [8], and the theory of Buchsbaum singularities is now developing (cf. [6], [7], [9], [10], and [12]).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 80 , December 1980 , pp. 107 - 116
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1980

References

[ 1 ] Goto, S. and Shimoda, Y., On Rees algebras over Buchsbaum rings, in preprint.CrossRefGoogle Scholar
[ 2 ] Goto, S. and Watanabe, K., On graded rings, II, Tokyo J. Math., 1–2 (1978), 237–261.Google Scholar
[ 3 ] Hochster, M., Rings of invariants of tori, Cohen-Macaulay rings generated by monomials, and polytopes, Ann. Math., 96 (1972), 318–337.CrossRefGoogle Scholar
[ 4 ] Matijevic, J. and Roberts, P., A conjecture of Nagata on graded Cohen-Macaulay rings, J. Math. Kyoto Univ., 14 (1974), 125–128.Google Scholar
[ 5 ] Renschuch, B., Stückrad, J., and Vogel, W., Weitere Bemerkungen zu einem Problem der Schnittheorie und über ein Maß von A. Seidenberg für die imperfektheit, Algebra, J., 37 (1975), 447–471.CrossRefGoogle Scholar
[ 6 ] Schenzel, P., On Veronesean embeddings and projections of Veronesean varieties, Archiv der Mathematik, 30 (1978), 391–397.CrossRefGoogle Scholar
[ 7 ] Schenzel, P., Applications of dualizing complexes to Buchsbaum rings, in preprint.CrossRefGoogle Scholar
[ 8 ] Stückrad, J. and Vogel, W., Eine Verallgemeinerung der Cohen-Macaulay Ringe und Anwendungen auf ein Problem der Multiplizitätstheorie, J. Math. Kyoto Univ., 13–3 (1973), 513–528.Google Scholar
[9] Stückrad, J. and Vogel, W., Toward a theory of Buchsbaum singularities, Amer. J. Math., 100 (1978), 727–746.CrossRefGoogle Scholar
[10] Stückrad, J. and Vogel, W., On Segre products and applications, Algebra, J., 54 (1978), 374–389.CrossRefGoogle Scholar
[11] Valla, G., Certain graded algebras are always Cohen-Macaulay, Algebra, J., 42 (1976), 537–548.CrossRefGoogle Scholar
[12] Vogel, W., A non-zero-divisor characterization of Buchsbaum modules, in preprint.CrossRefGoogle Scholar