Published online by Cambridge University Press: 22 January 2016
In this paper, we shall consider the logarithmic potential
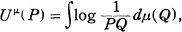
where μ is a positive measure in the plane, P and Q are any points and PQ denotes the distance from P to Q. In general, consider the potential
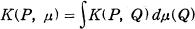
of a positive measure μ taken with respect to a kernel K(P, Q) which is a continuous function in P and Q and may be + ∞ for P = Q. A kernel K (P, Q) is said to satisfy the balayage principle if, given any compact set F and any positive measure μ with compact support, there exists a positive measure μ′ supported by F such that K(P, μ′) = K(P, μ) on F with a possible exception of a set of k-capacity zero and K(P, μ′)≦K(P, μ) everywhere. A kernel K(P, Q) is said to satisfy the equilibrium principle if, given any compact set F there exists a positive measure λ supported by F such that K(P, λ) = V (a constant) on F with a possible exception of a set of K-capacity zero and K(p, λ)≦V everywhere.