Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T07:31:31.676Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Auslander-Reiten quiver of an infinitesimal group

Published online by Cambridge University Press:  22 January 2016

Rolf Farnsteiner
Rolf Farnsteiner*
Affiliation:
Department of Mathematics, University of Wisconsin Milwaukee, WI 53201, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

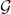Let be an infinitesimal group scheme, defined over an algebraically closed field of characteristic p. We employ rank varieties of 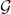-modules to study the stable Auslander-Reiten quiver of the distribution algebra of 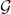. As in case of finite groups, the tree classes of the AR-components are finite or infinite Dynkin diagrams, or Euclidean diagrams. We classify the components of finite and Euclidean type in case 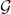is supersolvable or a Frobenius kernel of a smooth, reductive group.

Keywords

16G7014L20
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 160 , 2000 , pp. 103 - 121
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2000

References

[1] Auslander, M., Reiten, I. and Smalø, S., Representation Theory of Artin Algebras, Cambridge Studies in Advanced Math., Cambridge University Press, 36, 1995.Google Scholar
[2] Ballard, J., Injective modules for restricted enveloping algebras, Math. Z., 163 (1978), 57–63.Google Scholar
[3] Benson, D., Representations and Cohomology I, Cambridge Studies in Advanced Mathematics, 30, Cambridge University Press, 1991.Google Scholar
[4] Benson, D., Representations and Cohomology II, Cambridge Studies in Advanced Math ematics, 31, Cambridge University Press, 1991.Google Scholar
[5] Butler, M. and Ringel, C., Auslander-Reiten sequences with few middle terms and applications to string algebras, Comm. Algebra, 15 (1987), 145–179.Google Scholar
[6] Demazure, M. and Gabriel, P., Groupes Algébriques I, Masson/North Holland, 1970.Google Scholar
[7] Erdmann, K., Blocks of Tame Representation Type and Related Algebras, Lecture Notes in Mathematics 1428, Springer Verlag, 1990.Google Scholar
[8] Erdmann, K., On Auslander-Reiten components for group algebras, J. Pure Appl. Algebra, 104 (1995), 149–160.Google Scholar
[9] Erdmann, K., The Auslander-Reiten quiver of restricted enveloping algebras, CMS Conf. Proc., 18 (1996), 201–214.Google Scholar
[10] Erdmann, K. and Skowroński, A., On Auslander-Reiten components of blocks and self-injective special biserial algebras, Trans. Amer. Math. Soc., 330 (1992), 165–189.Google Scholar
[11] Farnsteiner, R., Periodicity and representation type of modular Lie algebras, J. reine angew. Math., 464 (1995), 47–65.Google Scholar
[12] Farnsteiner, R., On the distribution of AR-components of restricted Lie algebras, Contemp. Math., 229 (1998), 139–157.Google Scholar
[13] Farnsteiner, R., On Auslander-Reiten quivers of enveloping algebras of restricted Lie alge bras, Math. Nachr., 202 (1999), 43–66.Google Scholar
[14] Farnsteiner, R., On support varieties of Auslander-Reiten components, Indag. Math., 10 (1999), 221–234.Google Scholar
[15] Farnsteiner, R., Auslander-Reiten components for Lie algebras of reductive groups, Adv. in Math., 155 (2000), 49–83.Google Scholar
[16] Farnsteiner, R. and Voigt, D., Modules of solvable infinitesimal groups and the structure of representation-finite cocommutative Hopf algebras, Math. Proc. Cambridge Philos. Soc., 127 (1998), 441–459.Google Scholar
[17] Farnsteiner, R. and Voigt, D., On cocommutative Hopf algebras of finite representation type, Adv. in Math., 155 (2000), 1–22.Google Scholar
[18] Fischman, D., Montgomery, S. and Schneider, H., Frobenius extensions of subalgebras of Hopf algebras, Trans. Amer. Math. Soc., 349 (1996), 4857–4895.Google Scholar
[19] Friedlander, E. and Suslin, A., Cohomology of finite group schemes over a field, Invent. math., 127 (1997), 209–270.Google Scholar
[20] Happel, D., Preiser, U. and Ringel, C., Vinberg’s characterization of Dynkin diagrams using subadditive functions with applications to DTr-periodic modules, In: Representation Theory II, Springer Lecture Notes in Mathematics, 832 (1981), 280–294.Google Scholar
[21] Huppert, L., Homological characteristics of pro-uniserial rings, J. Algebra, 69 (1981), 43–66.Google Scholar
[22] Jantzen, J., Representations of algebraic groups, Pure and Applied Mathematics, 131, Academic Press, 1987.Google Scholar
[23] Kupisch, H., Beträge zur Theorie nichthalbeinfacher Ringe mit Minimalbedingung, J. reine angew. Math., 201 (1959), 100–112.Google Scholar
[24] Larson, R. and Sweedler, M., An associative orthogonal bilinear form for Hopf algebras, Amer. J. Math., 91 (1969), 75–94.Google Scholar
[25] Pfautsch, W., Die Kocher der Frobeniuskerne der SL2 , Dissertation, Universität Bielefeld, 1983.Google Scholar
[26] Suslin, A., Friedlander, E. and Bendel, C., Infinitesimal 1-parameter subgroups and cohomology, J. Amer. Math. Soc., 10 (1997), 693–728.Google Scholar
[27] Suslin, A., Friedlander, E. and Bendel, C., Support varieties for infinitesimal group schemes, J. Amer. Math. Soc., 10 (1997), 729–759.Google Scholar
[28] Sweedler, M., Hopf Algebras, W.A. Benjamin, Inc., New York, 1969.Google Scholar
[29] Waterhouse, W., Introduction to affine group schemes, Graduate Texts in Mathematics, 66, Springer Verlag, 1979.Google Scholar
[30] Webb, P., The Auslander-Reiten quiver of a finite group, Math. Z., 179 (1982), 97–121.Google Scholar