Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-11T05:42:13.063Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE ASYMPTOTIC BEHAVIOR OF THE VASCONCELOS INVARIANT FOR GRADED MODULES

Part of: Commutative algebra: Homological methods General commutative ring theory

Published online by Cambridge University Press:  10 February 2025

LUCA FIORINDO Open the ORCID record for LUCA FIORINDO [Opens in a new window]  and
DIPANKAR GHOSH Open the ORCID record for DIPANKAR GHOSH [Opens in a new window]
LUCA FIORINDO*
Affiliation:
Dipartimento di Matematica, Dipartimento di Eccellenza 2023-2027 Università di Genova Genova - 16146 Italy
DIPANKAR GHOSH
Affiliation:
Department of Mathematics Indian Institute of Technology Kharagpur Kharagpur - 721302, West Bengal India [email protected], [email protected]
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The notion of Vasconcelos invariant, known in the literature as v-number, of a homogeneous ideal in a polynomial ring over a field was introduced in 2020 to study the asymptotic behavior of the minimum distance of projective Reed–Muller type codes. We initiate the study of this invariant for graded modules. Let R be a Noetherian 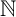$\mathbb {N}$-graded ring and M be a finitely generated graded R-module. The v-number $v(M)$ can be defined as the least possible degree of a homogeneous element x of M for which 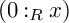$(0:_Rx)$ is a prime ideal of R. For a homogeneous ideal I of R, we mainly prove that 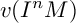$v(I^nM)$ and 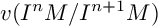$v(I^nM/I^{n+1}M)$ are eventually linear functions of n. In addition, if 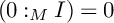$(0:_M I)=0$, then 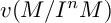$v(M/I^{n}M)$ is also eventually linear with the same leading coefficient as that of $v(I^nM/I^{n+1}M)$. These leading coefficients are described explicitly. The result on the linearity of 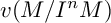$v(M/I^{n}M)$ considerably strengthens a recent result of Conca which was shown when R is a domain and 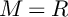$M=R$, and Ficarra–Sgroi where the polynomial case is treated.

Keywords

Graded rings and modulesAssociate primesv-numbersCastelnuovo–Mumford regularity

MSC classification

Primary: 13A02: Graded rings 13A15: Ideals; multiplicative ideal theory 13A30: Associated graded rings of ideals (Rees ring, form ring), analytic spread and related topics 13D45: Local cohomology
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bagheri, A., Chardin, M. and Hà, H. T., The eventual shape of Betti tables of powers of ideals , Math. Res. Lett. 20 (2013), 1033–1046.Google Scholar
Biswas, P. and Mandal, M., A study of v-number for some monomial ideals , Collect. Math. 2024, https://doi.org/10.1007/s13348-024-00451-x.CrossRefGoogle Scholar
Brodmann, M., Asymptotic stability of $Ass\left(M/{I}^nM\right)$ , Proc. Amer. Math. Soc. 74 (1979), 16–18.Google Scholar
Bruns, W., Conca, A., Raicu, C. and Varbaro, M., Determinants, Gröbner Bases and Cohomology, Springer Monographs in Mathematics, Springer, Cham, 2022.CrossRefGoogle Scholar
Bruns, W., Conca, A. and Varbaro, M., “Castelnuovo-Mumford regularity and powers”, in Commutative Algebra: Expository Papers Dedicated to David Eisenbud on the Occasion of his 75th Birthday, Springer, Cham, 2022, 147–158.CrossRefGoogle Scholar
Bruns, W. and Herzog, J., Cohen-Macaulay Rings, Cambridge Studies in Advanced Mathematics, vol. 39, Cambridge University Press, Cambridge, 1993.Google Scholar
Chardin, M., Ghosh, D. and Nemati, N., The (ir)regularity of Tor and Ext , Trans. Amer. Math. Soc. 375 (2022), 47–70.CrossRefGoogle Scholar
Civan, Y., The v-number and Castelnuovo-Mumford regularity of graphs , J. Algebraic Combin. 57 (2023), 161–169.CrossRefGoogle Scholar
Conca, A., A note on the v-invariant , Proc. Amer. Math. Soc. 152 (2024), 2349–2351.Google Scholar
Cooper, S. M., Seceleanu, A., Tohǎneanu, S. O., Pinto Vaz, M. and Villarreal, R. H., Generalized minimum distance functions and algebraic invariants of Geramita ideals , Adv. Appl. Math. 112 (2020), 101940, 34 pp.CrossRefGoogle Scholar
Cutkosky, S. D., Herzog, J. and Trung, N. V., Asymptotic behaviour of the Castelnuovo–Mumford regularity , Compositio Math. 118 (1999), 243–261.CrossRefGoogle Scholar
Ene, V. and Herzog, J., Gröbner Bases in Commutative Algebra, Graduate Studies in Mathematics, Vol. 130, American Mathematical Society, Providence, RI, 2012.Google Scholar
Ficarra, A. and Sgroi, E., Asymptotic behaviour of the v-number of homogeneous ideals, Preprint, 2023, arXiv:2306.14243.Google Scholar
Grayson, D. R. and Stillman, M. E., Macaulay2, a software system for research in algebraic geometry, http://www2.macaulay2.com Google Scholar
Jaramillo, D. and Villarreal, R. H., The v-number of edge ideals , J. Combin. Theory Ser. A 177 (2021), 105310.CrossRefGoogle Scholar
Katz, D. and West, E., A linear function associated to asymptotic prime divisors , Proc. Amer. Math. Soc. 132 (2004), 1589–1597.CrossRefGoogle Scholar
Kodiyalam, V., Asymptotic behaviour of Castelnuovo-Mumford regularity , Proc. Amer. Math. Soc. 128 (2000) 407–411.CrossRefGoogle Scholar
McAdam, S. and Eakin, P., The asymptotic ass , J. Algebra 61 (1979), 71–81.CrossRefGoogle Scholar
Saha, K., The v-Number and Castelnuovo-Mumford regularity of cover ideals of graphs , Int. Math. Res. Not. IMRN, 2023, rnad277.Google Scholar
Saha, K. and Sengupta, I., The v-number of monomial ideals , J. Algebraic Combin. 56 (2022), 903–927.CrossRefGoogle Scholar
Trung, N. V. and Wang, H.-J., On the asymptotic linearity of Castelnuovo-Mumford regularity , J. Pure Appl. Algebra 201 (2005), 42–48.CrossRefGoogle Scholar
West, E., Primes associated to multigraded modules , J. Algebra 271 (2004), 427–453.CrossRefGoogle Scholar